머신러닝
-
텐서플로우 - Linear regression 코드 정리2019.04.03
모두를 위한 딥러닝 (sung kim) lec5 - Logistic Classification (로지스틱 회귀분석)

이번 포스팅에서는, Logistic (regression) classification에 대해 알아볼 것입니다.
(왜 중간에 (regression)이 있는지는 나중에 다룰게요!)

우선 Logistic (regression) classification이 정확히 뭔지 알아보기 전에, 일단 Binary Classification이 뭐였는지 먼저 알아봅시다.
Binary Classification은 두개로 이루어진 값들을 분류하는 작업입니다.
가령 스팸메일 필터링을 한다고 했을 때는, 이 메일이 스팸인지 그냥 메일인지 확인해야 하겠죠?
이 때 이 메일을 스팸인지/그냥 메일인지 두 가지중 하나로 분류하는 작업을 바로 Binary Classification이라고 합니다.

그런데 이런 작업을 할 때, 어떤 메일이 스팸인지 / 그냥 메일인지 구분할 때 0과 1로 인코딩 작업을 거칩니다.
가령 스팸이면 1, 그냥 메일이면 0으로 두는 것이죠.
그런데 왜 이렇게 인코딩을 할까요?
왜 이러는지는 regression의 성질을 생각하면 조금 이해가 될 듯 합니다.
(우리가 배우는 모델은 classification 작업에 사용될 뿐이지, 엄연히 regression모델입니다!!!)
저번 시간까지 배웠던 linear regression의 결과값은 어떻게 나왔나요?
가령 성적을 예측하는 regression모델이라고 한다면, 예측한 점수를 결과값으로 내게 될 것입니다.
이렇듯, regression모델은 특정한 '값'을 '예측'하는데 사용됩니다.
그렇기 때문에 이런 regression 모델로 분류를 진행하려면, 이런 class들을 (스팸인지 아닌지) '값'으로 설정해야 합니다.
스팸 메일은 1, 그냥 메일은 0.. 이렇게 말이죠.
그리고 그렇게 예측한 값이 1에 가깝다면 스팸메일이다! 라고 예측을 하고,
예측한 값이 0에 가깝다면 진짜 메일이다! 라고 예측을 하는 겁니다.

그런데, 그럼 그냥 Linear regression 모델을 그냥 사용하면 안되는 걸까요? 안되니깐 다른 모델을 배우는거겠죠?
자, 위의 예시를 봅시다.
위의 그래프는 x축에 공부한 시간, y축에 pass / fail (1 / 0)이 그려진 그래프로,
공부한 시간 비례 시험에서 통과할지 실패할지 예측하는 모델을 그린 것입니다.
그럼 이것을 Linear regression모델로 짤 수도 있지 않을까요?
fail 과 pass를 나누는 직선 하나를 그린 뒤에,
그 직선의 y값이 0.5 이하이면 fail, 아니면 pass라고 하면 잘 작동할것 처럼 보이기도 합니다.
그런데, 저 오른쪽 끝부분 (아래에 50적혀있는) 의 동그라미를 봅시다.
만약 어떤 학생이 정말 시험에서 너무 pass하고 싶어서 50시간이나 공부를 해서 pass를 받았다고 가정해 봅시다.
그러면 어떤 문제점이 발생하느냐 하면,
linear regression의 Hypothesis H(x) = WX + B 함수가 저 오른쪽의 동그라미도 감안하고 측정이 되므로,
저 동그라미가 없을때보다 직선이 조금 더 오른쪽 아래로 기울어지는 현상이 발생합니다.
그런데 이렇게 되면 원래는 pass였던 것들의 y값이 0.5 아래로 내려가버리면서 fail로 처리되는 문제가 발생하게 됩니다.
(위의 그래프에 그려진 파란 직선 두개 참고)
이렇듯, Binary classification (사실 classification 전체 다)를 수행하는 데 Linear Regression 모델은 적합하지 못합니다.

Linear regression을 사용하기 애매한 이유가 또 있습니다.
Linear regression의 경우 Hypothesis 함수를 H(x) = Wx + b 로 정의합니다. 그쵸?
그런데 어차피 y값들 (class, 스팸인지 아닌지)는 0이거나 1이 된다는 것을 우리는 이미 알고 있습니다.
(0, 1 인코딩을 이미 했고, 그렇게 분류하는것이 binary classification의 목적이니까요.)
그런데 Linear regression의 H(x)는 1보다 엄청 큰 수를 결과값으로 뱉을 수도 있고, 0보다 엄청 작은 수를 결과값으로 뱉을 수 있습니다.
가령 H(x) = 100x 라는 hypothesis가 있다고 해봅시다.
우리의 목적은 데이터들을 0과 1 둘중 하나의 값으로 분류하는 것이 목적이므로,
1에 가까운 값은 1로 분류하고, 0에 가까운 값은 0으로 분류하게 될 것입니다.
그런데 H(x) = 100x가 되버리면 (대략적으로) x가 0.01 이상일때는 모두 1로, x가 0 이하일때는 모두 0으로 분류되게 됩니다.
이러면 어떤 문제점이 발생해 버리냐하면, x값에 너무 민감하게 반응하는 모델이 만들어지게 됩니다.
즉, 연산상으로는 매우 작은 값(0.01)만 바뀌어도 아예 분류 자체가 바뀌어버리게 되는 것입니다.
이는 아까 위에서 설명했던 문제와 겹치며 linear regression 모델을 classification을 하는 용도로 사용하기 힘들게 만듭니다.

이를 해결하기 위하여 나온 것이 바로 logistic function (sigmoid function 이라고도 한다) 입니다.
원래 linear하던 H(x) = wx + b를 0과 1 사이의 함수로 바꿔주는 함수입니다.
수식으로 나타낸다면, g(z) = 1 / (1+ e^-z) 가 됩니다.
이렇게 hypothesis에 sigmoid 함수를 씌워주면, 무슨 함수였던지간에 결과값이 모두 0과 1 사이로 나오는 함수를 만들어 줄 수 있습니다.
(왜 이런 값이 나오는지 수학적으로 설명하는 것은 나중에 부록 편에서 다루겠습니다.)

그리고 이것을 Logistic regression의 Hypothesis로 나타낸다면 위와 같은 수식으로 나타내어 집니다.
(W T X 는 그냥 간단하게 W * X로 생각해 주시면 됩니다.
multi-variable의 경우에서도 사용할 수 있도록 만든 hypothesis인지라 저런 식이 들어갑니다.)
그리고 이렇게 H(x)의 값이 0과 1사이로 나오면, 사용하기에 매우 편리해 지게 됩니다.
위의 Hypothesis 함수로 regression을 한 결과값이 0.5이상인 경우엔 1로 분류하고, 0.5보다 작으면 0으로 분류하면 되는 것이죠.
(사실 아까 전에 0,1 encoding을 한 이유도 이것 때문입니다.)
*참고 : Logistic "Regression" 인 이유!
많은 분들이 왜 이 모델이 Regression 모델인지 헷갈려 하곤 합니다.
그러니까, Logistic regression은 사실 classification을 하는데 사용하는데, 왜 regression이라고 불리는가를 헷갈려 하는 것이죠.
하지만 Logistic regression모델은 결과값이 0과 1 사이로 한정되는 특성상 classification을 하는 데 사용되는 모델이긴 하지만, 결과값으로 특정한 "값"을 도출해내는 모델입니다.
가령, 성적을 예측하는 Linear regression은 점수 그 자체를 결과값으로 도출합니다. (10점, 30점, 60점 등등...)
그와 비슷하게 스팸 메일인지 아닌지를 분류하는 Logistic regression 모델은 0과 1 사이의 값 자체를 결과로 냅니다. (0, 0.2, 0.8 등등...)
그러니까, Logistic Regression은 입력값 x에 대해 0과 1로만 이루어진 y값에 최대한 가깝게 그려질 수 있는 함수를 만들어내는 모델인 것입니다.
그리고 결과값이 0.5보다 큰 (즉, 1에 가까운) 값들은 죄다 1로 분류해 버리는 것이고,
결과값이 0.5보다 작은 (즉, 0에 가까운) 값들은 죄다 0으로 분류해 버리는 것입니다.
그러니깐 그냥 이제부터 Logistic (regression) classification이 아니라
logistic regression모델이라고 부르겠습니다.

그런데, 이렇게 Hypothesis를 바꿔버리면 원래 쓰던 cost function은 사용하지 못합니다.
왜냐 하면, 원래 쓰던 Cost function을 여기다가도 적용해버리면 non-convex한 function이 나오게 되기 때문입니다.
(cost function이 convex function이어야 하는 이유는 2강 (https://cding.tistory.com/21) 에서 다뤘습니다!)
+ 왜 그렇게 되는지는 나중에 부록편에서 따로 더 설명하겠습니다.
그래서 logistic regression의 cost function은 따로 만들어 줘야 합니다.
logistic regression의 cost function은 다음과 같이 정의합니다 :
y=1일때 c(H(x), y) = -log(H(x))
y=0일때 c(H(x), y) = -log(1 - H(x))
(단, 여기서 log는 상용로그가 아니라 자연상수 e를 밑으로 갖는 자연로그입니다.)
그런데 왜 cost function을 이렇게 정의했느냐를 제대로 설명하려면 엄청난 수학의 압박이 느껴지게 됩니다...
그러니 일단 지금은 직관적으로 왜 cost function을 이렇게 정의하는지만 알아봅시다.

그냥 지금 간단하게 생각해 봅시다.
(위의 그래프들은 x축에 h(x)값, y축에 cost 값을 나타내는 그래프입니다!!)
일단 y=1인 경우, 즉 h(x) = 1인 경우엔 왜 cost function은 -log(H(x))가 될까요?
(왼쪽 그래프 참고)
h(x)값이 0에서 1으로 이동하면 cost 값은 ∞에서 0으로 점점 줄어들게 되는 것을 확인할 수 있습니다.
즉, h(x)가 정답인 1로 가면 갈수록 cost는 줄어들고, 오답인 0으로 가면 갈수록 cost가 늘어납니다.
이러면 우리가 원하는 합리적인 cost function이 완성된 것이겠죠?
반대로, y=0인 경우, 즉 h(x) = 0인 경우에 cost function이 -log(1-H(x)) 인 이유도 동일합니다.
h(x)값이 1에서 0으로 이동하면 cost 값은 ∞에서 0으로 점점 줄어들게 되는 것을 확인할 수 있습니다.
즉, 이번에는 h(x)가 정답인 0로 가면 갈수록 cost는 줄어들고, 오답인 1으로 가면 갈수록 cost가 늘어납니다.
그냥 이정도로만 이해해 주시고, 왜 cost function을 이렇게 설정했는지는 나중에 부록 편에서 다루겠습니다.

그리고 위처럼 y=1일때와 y=0일때로 나누어도 좋겠지만,
직접 컴퓨터로 연산을 할 때는 간단한 수식으로 나타내는 것이 훨씬 좋겠죠?
그래서 나온 공식의 위의 파란 박스가 쳐진 수식입니다.
어려울것 하나 없습니다!
y=0일 때는 -y * log(H(x)) 부분이 0이 되면서 자연스럽게 -log(1 - H(x)) 라는 cost function이 나오게 되고,
y=1일 때는 (1-y) * log(1 - H(x)) 부분이 0이 되면서 자연스럽게 -log(H(x)) 라는 cost function이 나오게 됩니다.
그리고 컴퓨터로 연산을 할 때는 if문을 사용해서 y==1인 경우와 y==0인 경우로 나누지 않고,
그냥 위의 수식을 사용하게 될 것입니다.

(위의 ppt의 Gradient decent는 오타입니다...ㅎㅎ;)
Gradient descent는 그냥 다른 모델과 동일하게 cost(W)를 W에 대해 미분하는 것으로 적용하면 됩니다.
그리고 이를 tensorflow를 사용해서 코드로 적용할 때는 그냥 GradientDescentOptimizer(a) 로 적용하면 됩니다.
(실제 cost값을 미분하면 어떤 값이 나오는지는 그냥 설명하지 않겠습니다. 매우 불필요합니다. 부록에서도 설명 안할듯)
이렇게 Logistic regression에 대해서 알아봤습니다.
사실 이렇게만 설명해도 Logistic regression이 어떤 개념인지는 모두 이해하셨으리라 믿지만,
나중에 부록편에서 조금 더 수학적으로 접근해서 왜 cost function이 저렇게 나오는지 설명하겠습니다.
그럼 다음엔 softmax regression (multinomial classification)으로 찾아뵙겠습니다!
'인공지능 > 모두를 위한 딥러닝 (sung kim) lec' 카테고리의 다른 글
| 모두를 위한 딥러닝 부록편 - 미분의 개념과 Gradient Descent (1) | 2019.05.10 |
|---|---|
| 모두를 위한 딥러닝 (sung kim) lec4 - Multivariable Linear Regression (다변수 선형 회귀) (1) | 2019.04.09 |
| 모두를 위한 딥러닝 (sung kim) lec3 - Gradient Descent (경사하강법) (0) | 2019.04.08 |
| 모두를 위한 딥러닝 (sung kim) lec2 - Linear regression & cost function (0) | 2019.03.30 |
| 모두를 위한 딥러닝 (sung kim) lec1 - 머신 러닝 기초 (0) | 2019.03.28 |
모두를 위한 딥러닝 (sung kim) lec4 - Multivariable Linear Regression (다변수 선형 회귀)

이번 포스팅에서는, Multivariable Linear Regression, 즉 다변수 선형 회귀에 대해서 알아보겠습니다.

일단 저번 시간까지 했던 내용들을 복습해 보겠습니다.
일반적인 Linear Regression의 Hypothesis는 H(x) = Wx + b였죠?
Cost function은 H(x) - y를 제곱해서 모두 더한 뒤 평균값을 내주는 것이었고...
Gradient Descent는 가장 적절한 (cost(W) 값이 가장 작은) W값을 찾아내는 알고리즘이었습니다.
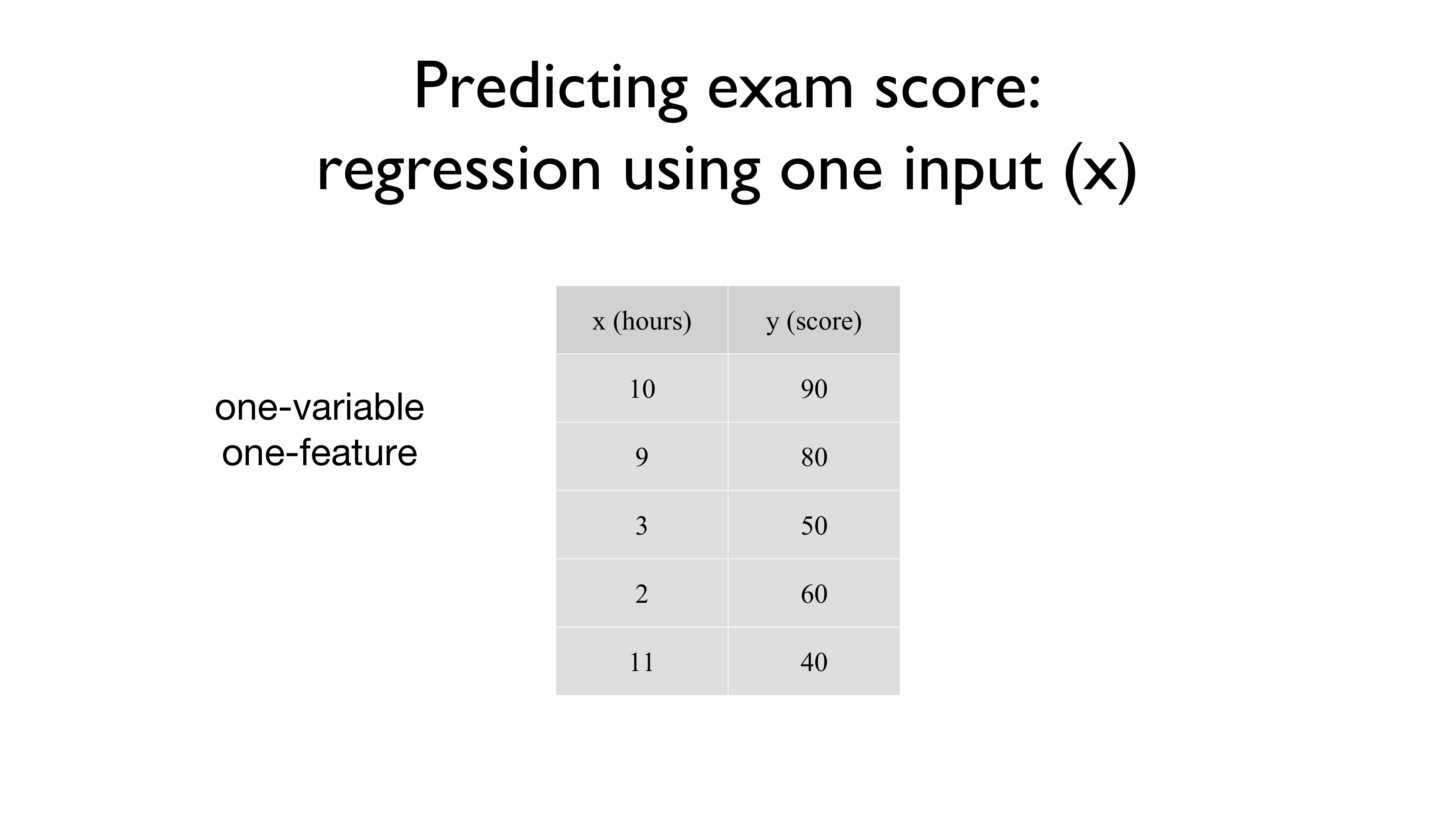
그리고 우리가 마주했던 데이터들은 다들 이런 형식으로 생겼습니다.
x값 하나당 y값 하나가 주어지는 형식이었죠.
이때, x는 하나의 feature을 의미합니다.
가령, 위의 경우엔 특정 점수 y를 그 점수를 갖게 되었던 특징인 feature x를 통해 알아봤던 것이죠.
그래서 위의 사진에서 one-variable one-feature라고 적혀있는 것입니다.
변수 하나에 특징도 하나밖에 (공부한 시간) 없으니까요.

그런데, 오늘 배울 Multi-variable Linear Regression은 데이터가 조금 다르게 들어옵니다.
x값이 하나가 아니라, 두 개, 세 개, 혹은 10000개도 들어오는데요,
각각의 x값 (x1, x2, x3)들은 각자의 특성을 띄고 있습니다.
위의 예시의 경우 x1 은 quiz1의 점수,
x2는 quiz2의 점수,
x3는 중간고사 1의 점수이고
이 점수들을 모두 어떠한 방식으로 계산했을 때 최종 점수인 Y가 나오게 되는 것입니다.

그런데, 그렇게까지 어려워지진 않았습니다!
Linear Regression의 기본형인 H(x) = Wx + b 를 그대로 따라서,
H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b
로 약간만 변형되었을 뿐입니다.
잠깐만 살펴보면, x의 종류 (feature의 개수)가 늘어나면, 그에 따라 w의 개수도 늘어나게 됩니다!
x1에는 w1, x2에는 w2, x3에는 w3를 곱해주는 식으로 말이죠.
그리고, b의 값은 여전히 그대로 남아있습니다.
feature가 많아졌다고 해서 b의 개수도 많아지진 않은 것이죠.
(그도 당연한 것이, 각자의 x값에 b를 더하더라도 어차피 상수 하나 더한 거랑 같으니까요.)

그럼, Cost function은 어떻게 바뀌었을까요?
H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b
를 그대로 우리가 사용하던 Cost function 안에 집어넣으면 됩니다.
즉, H(x1, x2, x3) - y 를 제곱한 것을 모두 더해서 평균을 내는 것이죠.
조금만 더 풀자면, H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b 이므로,
w1x1 + w2x2 + w3x3 + b - y 를 제곱해서 모두 더해주는 것이죠.

그리고 x1, x2, x3와 같이 feature의 개수가 세 개가 아니고 무수히 많더라도, 위의 식처럼
H(x1, x2, x3,... , xn) = w1x1 + w2x2 + w3x3 +... + wnxn + b
로 표현이 가능합니다.
즉, 우리가 원래 알고 있던 Linear Regression의 식을 아주 쬐끔만 변형시켜 주면,
Multi-variable Linear Regression도 뚝딱 해낼 수 있습니다.
그런데, 중요한 것은 그게 아니고,
"그래서 이거 계산 어떻게 할건데?"입니다.
그러니깐, 기본적인 Linear Regression에서는 x값이 10개 정도 주어지고, w값이 하나니깐
x1 * w + x2 * w + x3 * w +... + x10 * w + b
정도로 계산이 가능했고, 그냥 {x1, x2, x3,... , x10} * w + b만 해도 되었습니다.
하지만, feature이 많아져서, 상황이 조금 달라졌습니다.
x1의 첫 번째 데이터를 x11, x3의 네 번째 데이터를 x34... 이런 식으로 쓰고, feature가 n개이고 데이터의 개수가 m 개라면 우리가 계산해야 할 식은
x11 * w1 + x21 * w2 +... + xn1 * wn + b
+ x12 * w1 + x22 * w2 +... + xn2 * wn + b
...
+ x1m * w1 + x2m * w2 +... + xnm * wn + b
처럼... 딱 봐도 복잡한 이차원 배열 * 일차원 배열을 계산해야 합니다.
하지만, 이것을 반복문으로 그냥 쭉 돌려버릴 수도 없는 것이...
가령 n과 m이 각각 10 만씩이라고만 해도,
반복문으로 돌리면 100억 번의 연산을 해야 한다는 말도 안 되는 결과가 나오기 때문입니다.
그러면 이것을 어떻게 간단하게 연산할 수 있을까요?
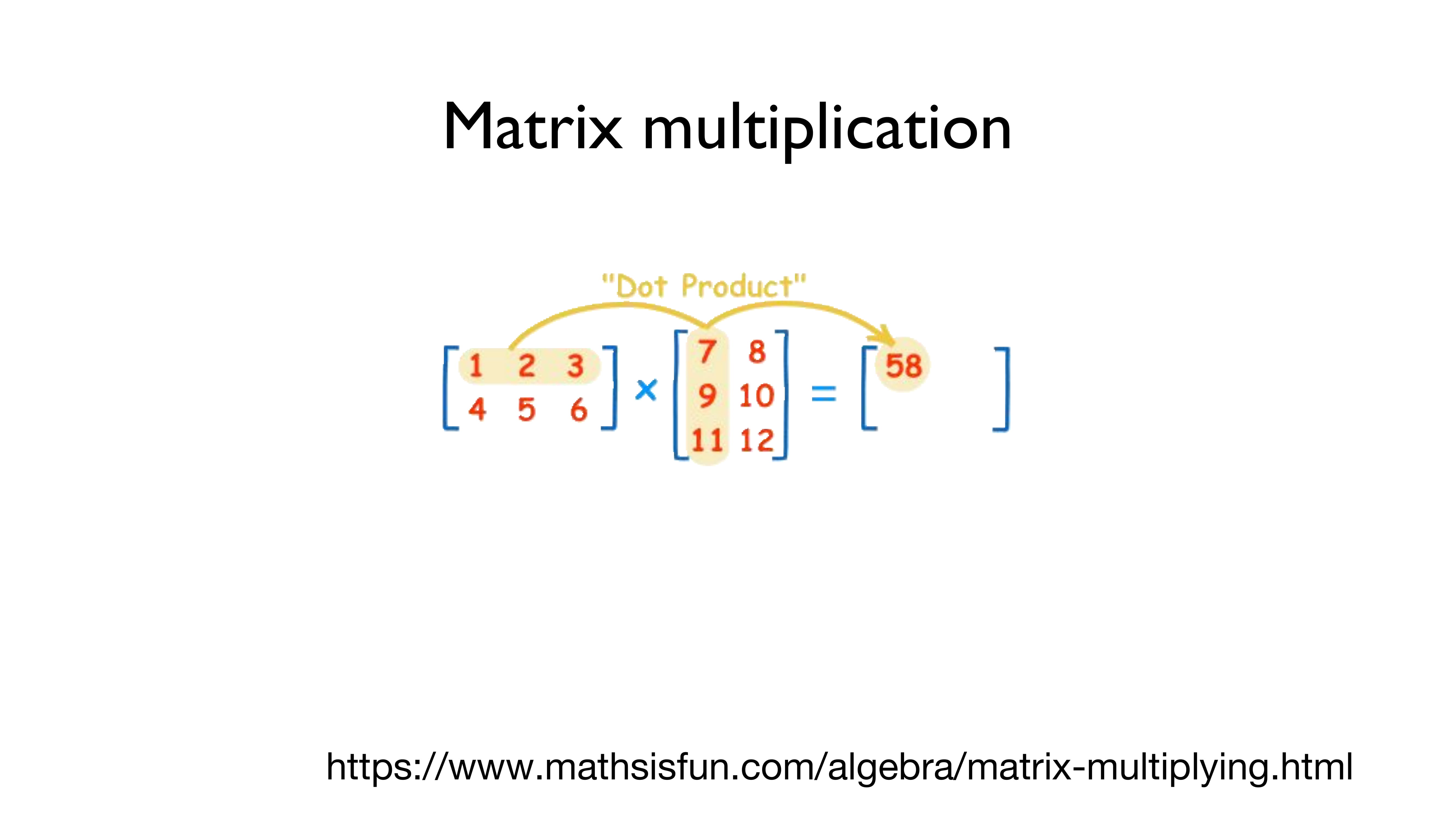
바로, "Matrix multiplication", 즉 "행렬곱"으로 이 문제를 해결합니다.
행렬곱은 어떤 식으로 진행되는지 위의 그림을 통해 알아봅시다.
(헷갈릴까 봐 써놓는데 - 가로가 행이고 세로가 열입니다!!!)
왼쪽의 [[1,2,3], [4,5,6]]의 (2,3)의 행렬과 [[7,8], [9,10], [11,12]]의 (3,2) 행렬을 곱하는 것은 간단합니다.
왼쪽의 행렬의 첫 번째 행인 [1,2,3]의 각각의 요소들을 오른쪽의 행렬의 첫 번째 열인 [7,9,11]로 곱해서 더해줍니다.
즉, 1*7 + 2*9 + 3*11 = 7 + 18 + 33 = 58
이 되는 겁니다.
그리고, 이 값을 결괏값의 행렬의 첫 번째 행, 첫 번째 열에 놓습니다.
두 번째도 동일하게 진행하면 됩니다.
왼쪽의 행렬의 첫 번째 행인 [1,2,3]의 각각의 요소들을 오른쪽의 행렬의 두 번째 열인 [8,10,12]로 곱해서 더해줍니다.
그러면, 1*8 + 2*10 + 3*12 = 8 + 20 + 36 = 64가 됩니다.
그리고, 이 값을 결괏값의 행렬의 첫 번째 행, 두 번째 열에 놓습니다.
두 번째 열은 직접 한번 해보시기 바랍니다.

자, 대충 배웠으니 한번 대충 적용해 봅시다.
w1x1 + w2x2 + w3x3을 행렬로 계산하려면 어떻게 해야 할까요?
x1, x2, x3를 (1,3)의 크기의 행렬로 놓고,
w1, w2, w3을 (3,1)의 크기의 행렬로 놓는다면,
행렬곱을 통해 x1 w1 + x2w2 + x3w3를 구할 수 있게 됩니다.

그런데, 우리가 가지고 있는 데이터는 x1, x2, x3값이 각각 하나만 들어있는 데이터가 아니죠?
x1 여러 개, x2 여러 개, x3 여러 개로 이루어진 데이터를 갖고 있는데, 이것을 어떻게 계산할까요?

아까 저 위에서 했던 짓을 똑같이 반복하면 됩니다.
우선, x값들의 행렬 중 첫 번째 행인 x11, x12, x13과 w1, w2, w3를 곱하여,
x11w1 + x12w2 + x13w3을 결괏값 행렬의 첫 번째 요소로 넣어줍니다.
그다음엔 x21w1 + w22w2 + w23w3 을 넣게 될 것이고,
그것을 마지막 데이터인 x51, x52, x53까지 반복하면 되는 것입니다.
그러면, 왼쪽의 x값의 데이터와 오른쪽의 w값의 데이터를 통해 결괏값을 행렬로 도출해 낼 수 있는 것이죠.

그런데 행렬곱에는 특징이 하나 있습니다.
입력되는 데이터의 형태에 따라 결괏값의 형태가 달라진다는 것이죠.
가령 바로 위의 예시를 보면, (5,3) 크기의 데이터와 (3,1) 크기의 데이터를 행렬곱하면, (5,1) 크기의 결괏값이 나오게 됩니다.
어떻게 보면 당연한 것이긴 합니다.
왼쪽의 (5,3) 행렬의 각각의 행을 오른쪽 (3,1)의 행렬에 곱해서 모두 더한 값은, 결괏값인 (5,1)의 행들에 집어넣고 있으니까요.
그런데, 여기서 중요한 점 하나가 더 있습니다!!
만약, (5,3) 크기의 행렬에 (2,1) 크기의 행렬을 행렬곱시키면 어떻게 될까요?
... 행렬곱 시킬 수 없습니다.. ㅎㅎ
이것도 어떻게 보면 당연한 것이겠지만,
x1, x2, x3를 w1, w2에만 곱할 수는 없는 노릇 아니겠습니까 ㅎㅎ
즉, 행렬곱을 계산해 줄 때에는 데이터의 크기를 잘 생각해야 합니다!
(n, m) 크기의 행렬을 x값으로 사용할 것이라면,
(m, 1) 크기의 행렬을 w값으로 사용해 주어야 한다는 것입니다.
그러면 결괏값은 (n, 1) 크기의 행렬로 나오게 되겠지요.

그런데, 중요한 게 또 또 있습니다!
행렬곱은 일반적인 곱셈과는 다르게 곱셈의 순서가 중요하다는 것입니다!
위의 식처럼, (5, 3) 크기의 행렬과 (3, 1)를 곱하면 (5, 1)이라는 행렬이 나오지만,
반대로 (3, 1) 크기의 행렬과 (5, 3) 크기의 행렬은 곱할 수 없다는 것입니다.
즉, 순서가 매우 매우 매우 중요합니다!!
앞 행렬의 행 크기와, 뒷 행렬의 열 크기가 동일해야 한다는 것입니다!
아까 전과 마찬가지로, (m, n)의 행렬에 곱할 수 있는 행렬은 (n , k) 꼴의 행렬뿐입니다.
(결괏값은 (m, k) 크기의 행렬로 나오겠죠.)



즉, 지금까지 하고 싶은 말이 무엇인고 하니...
우리가 Python이나 Tensorflow로 위의 Linear Regression을 구현하려면
지금까지 배웠던 H(x) = Wx + b 로 계산하는 것이 아니고,
H(X) = XW로 구현해야 한다는 것입니다!
이것을 특별히 더 강조한 이유는 간단합니다.
이거 처음 배울 때 저는 이 행렬 순서를 맞춰야 된다는 사실을 모른 채라 삽질을 오지게 했기 때문이죠 ㅎ
여러분들은 행렬의 크기를 맞추지 않아서 삽질하는 일은 없도록 합시다!

다음 포스팅에서는 Logistic Regression에 대해서 알아보겠습니다.
그럼 안녕!!
'인공지능 > 모두를 위한 딥러닝 (sung kim) lec' 카테고리의 다른 글
| 모두를 위한 딥러닝 부록편 - 미분의 개념과 Gradient Descent (1) | 2019.05.10 |
|---|---|
| 모두를 위한 딥러닝 (sung kim) lec5 - Logistic Classification (로지스틱 회귀분석) (0) | 2019.05.09 |
| 모두를 위한 딥러닝 (sung kim) lec3 - Gradient Descent (경사하강법) (0) | 2019.04.08 |
| 모두를 위한 딥러닝 (sung kim) lec2 - Linear regression & cost function (0) | 2019.03.30 |
| 모두를 위한 딥러닝 (sung kim) lec1 - 머신 러닝 기초 (0) | 2019.03.28 |
모두를 위한 딥러닝 (sung kim) lec3 - Gradient Descent (경사하강법)

안녕하세요.
이번 시간엔 머신 러닝의 꽃이라고 할 수 있는 Gradient Descent에 대해 알아봅시다.

저번 시간에 배웠던 내용을 잠시만 복습하고 들어가 봅시다.
우선, Linear Regression의 가설 함수는 H(x) = Wx + b 였고,
Cost function은 각각의 H(x) 값에서 y값(정답)을 빼준 후,
그 값들을 죄다 제곱해서 평균을 내주는 것이었습니다.
기억이 나지 않는다면, 이전 포스팅 (https://cding.tistory.com/12)에서 다시 한번 복습하고 와주세요!

그런데, 일단은 이해를 쉽게 하도록 하기 위해서 H(x)를 그냥 Wx라고 해봅시다.
(b를 빼준 것뿐, 일차함수라는 큰 틀은 변화하지 않았습니다.)
그러면, Cost function도 조금은 바뀌어서...
H(x)에서 y값을 빼주던 것을, Wx에서 y값을 빼주는 것으로 바꾸어도 상관없겠죠?
(H(x) = Wx 이므로)

그럼 이 상태에서 cost(W)의 값을 구해보도록 합시다.
X, Y가 왼쪽 표와 같이 주어진다면, 각각 W=1, W=0, W=2 일 때의 Cost값은 무엇일까요?
W=1일 경우,
X=1, Y=1에서 (W*x - y)^2 = (1 * 1 - 1)^2 = 0
X=2, Y=2에서 (W*x - y)^2 = (1 * 2 - 2)^2 = 0
X=3, Y=3에서 (W*x - y)^2 = (1 * 3 - 3)^2 = 0
이 세 가지 경우의 수를 모두 더하면 0+0+0 = 0, 평균으로 나눠도 0
즉, Cost(1) = 0입니다.
cost가 0이므로, W=1일 때 완벽하게 데이터에 들어맞는다는 뜻이죠.
W=0일 경우에는?
X=1, Y=1에서 (W*x - y)^2 = (2 * 1 - 1)^2 = 1
X=2, Y=2에서 (W*x - y)^2 = (2 * 2 - 2)^2 = 4
X=3, Y=3에서 (W*x - y)^2 = (2 * 3 - 3)^2 = 9
이 세 가지 경우의 수를 모두 더하면 1 + 4 + 9 = 14, 평균으로 나누면 14/3 = 4.66666...
즉, Cost(0) = 4.67입니다.
W=2 일 경우에는 어떨지, 직접 한번 해 보시길 바랍니다.
참고로, 답은 W=0일 때와 동일하게 4.67이 됩니다.

이렇듯, W값에 따라 cost(W)의 값은 변하게 됩니다.
W=1일 때 cost의 값은 0으로 최소가 되고,
W=2, W=0일 때 cost의 값은 약 4.67이 되는 식이죠.
이때, 이런 식으로 cost(W)에서 W의 값에 값들을 많이 집어넣게 되면 위의 그래프처럼 함수가 그려집니다.
(x축을 W로, y축을 Cost(W) 값으로 집어넣은 그래프입니다.)
위에서는 W=-3부터 W=5까지만 집어넣었지만, 다른 값들을 넣어도 여전히 이차함수의 그래프가 그려지게 되겠죠.
그런데, 어떻게 cost(W)의 값이 최소가 되는 W의 값을 구할 수 있을까요?

그래서 등장한 방법이 바로 Gradient Descent 알고리즘입니다.
(Gradient는 경사, Descent는 하강이므로 한국어로는 경사 하강법이라고 불립니다.)
위와 같은 상황에서 최소의 W값을 찾아주기 위한 알고리즘인데요,
굉장히 다양한 최소화 문제(특정 값을 최소화해주어야 할 때) 자주 사용되는 기법입니다.

일단은, Gradient Descent의 작동 방식에 대해 간단하게 먼저 알아봅시다.
우선, W를 랜덤 한 값으로 정해줍니다. (무엇으로 정해도 큰 상관은 없습니다.)
그런 후, 그 W의 값을 cost(W)의 값을 최소화시킬 수 있는 방향으로 바꿔줍니다. (보통 W값을 업데이트해준다고 표현합니다.)
그리고, 이 짓거리를 cost(W)가 최소가 될 때까지 반복합니다.
(저 위의 예시의 경우, W=1이 될 때까지 반복될 것입니다.)
그럼 여기서 당연히 의문이 하나 드실 것입니다.
"그래서 cost(W)의 값을 최소화시킬 수 있는 방향을 어떻게 아는데??"

자, 위의 사진에서 W의 값을 작은 공이라고 생각해 봅시다.
그러면, 공은 어느 방향으로 굴러가나요?
위의 경우, 경사가 왼쪽 아래로 져 있으므로 공은 왼쪽으로 굴러가게 될 것입니다.
그러면, 이 공은 어디까지 굴러갈까요?
cost(W) (위 이미지에선 J(w)라고 적혀있음)의 값이 가장 작아지는,
다시 말해서 가장 높이가 아래에 있는 곳까지 굴러갈 것입니다.
Gradient Descent는 이러한 원리와 동일하다고 봐도 됩니다.
W값이 처음 주어졌을 때, 우선 그 W값에 대한 경사를 먼저 구합니다.
그 후, 그 경사가 진 방향으로 W값을 바꿔줍니다.
경사가 왼쪽 방향으로 져 있다면, W값을 빼주고...
경사가 오른쪽 방향으로 져 있다면, W값을 더해주는 식으로 말이죠.
그렇게 한다면, 저 함수에서 가장 작은 cost(W)의 값을 가지는 W의 값을 구할 수 있게 됩니다.
Gradient Descent는 이렇게 단순한 생각을 갖고 만들어진 알고리즘입니다.
그런데, 그 각각의 W값에 대한 경사는 어떻게 구하냐고요?
그 경사를 구하기 위해서, 우리는 저 함수를 W값에 대하여 미분해 줄 것입니다.
(미분이 뭔지 잘 모르신다면, 간단하게 그냥 함수의 기울기를 구하는 방법 정도로 이해하시면 됩니다.)

지금부터의 내용은, 기본적으로 미분을 알고 있어야 이해가 가능합니다!
미분을 모르신다면, 그냥 저 아래로 쭉 내리시면 되겠습니다.
우선, f(x)^2를 미분하면 2 * f(x) * f'(x)가 됩니다.
그런데, 그 값에 그냥 m분의 1만 곱해버리면 상수 2가 남아버리니 계산하기 귀찮아지므로...
m분의 1 대신 2m분의 1을 곱하는 것으로 식을 바꾸겠습니다.

f(x)^2를 미분하면, 2 * f(x) * f'(x)가 된다는 사실을 이용하면,
(Wx - y)^2를 미분하면
2 * (Wx - y) * x 가 됩니다.
그리고 시그마 앞에선 2가 앞으로 넘어갈 수 있으므로,
2를 앞으로 넘기면 시그마 앞의 값은 1/2m * 2 = 1/m이 됩니다.
결국, W값은 W값에서 (Wx - y) * x의 평균을 낸 값을 뺀 값으로 업데이트해 줍니다. (위의 식 참고)
참고로, 위의 알파 값은 Learning Rate라는 것으로, 이에 대한 자세한 내용은 다른 시간에 알아봅시다.
Q. 왜 W값에서 "(Wx - y) * x의 평균을 낸 값"을 더하지 않고 빼는 것인가요?
A. 경사가 왼쪽을 향하고 있을 때, 그때의 미분 값은 양수인 가요, 음수인가요?
예, 경사가 왼쪽으로 져 있다면, 그 미분 값 (경사의 기울기 값)은 양수가 됩니다.
그런데 경사가 왼쪽으로 져 있으면, W값을 왼쪽으로 옮겨야겠죠? (즉, W값을 감소시켜야겠죠?)
그러므로, W값에서 양수를 빼주어야 W값이 감소하기 때문에, 저 값을 더하지 않고 빼는 것입니다.
반대로 경사가 오른쪽으로 져 있을 때에는 미분 값(기울기 값)이 음수가 되는데,
W값을 증가시켜 주어야 하므로,
음수를 빼주어서 W값을 증가시키는 것입니다.

그런데, 저 미분을 죄다 하고 있을 시간은 사람에게 없습니다.
그런 일 따위는 컴퓨터에게 시킬 수 있습니다.
즉, 미분 사실 몰라도 공식만 대충 집어넣으면 된다는 거죠,
(게다가 텐서 플로우를 비롯한 대부분의 머신러닝 툴에서는 Gradient Descent는 모두 지원합니다.)

그런데 만약 함수가 이따구로 생겼다면 어떻게 될까요?
어느 점에서 시작하느냐에 따라 경사가 진 곳이 죄다 다르므로, 향하는 방향이 죄다 다르게 됩니다.
결국, W값이 우리가 원하는 "함수 전체에서의 최솟값"으로 가는 것이 아니라,
"일정 구간만에서의 최솟값"으로 가게 됩니다.
이를 각각, "Global Minima"와 "Local Minima"라고 부릅니다.
아무튼, 저렇게 생긴 함수에선 그냥 W값이 Local Minima에 처박힐 가능성이 매우 높기에, Gradient Descent의 성능이 매우 떨어집니다.
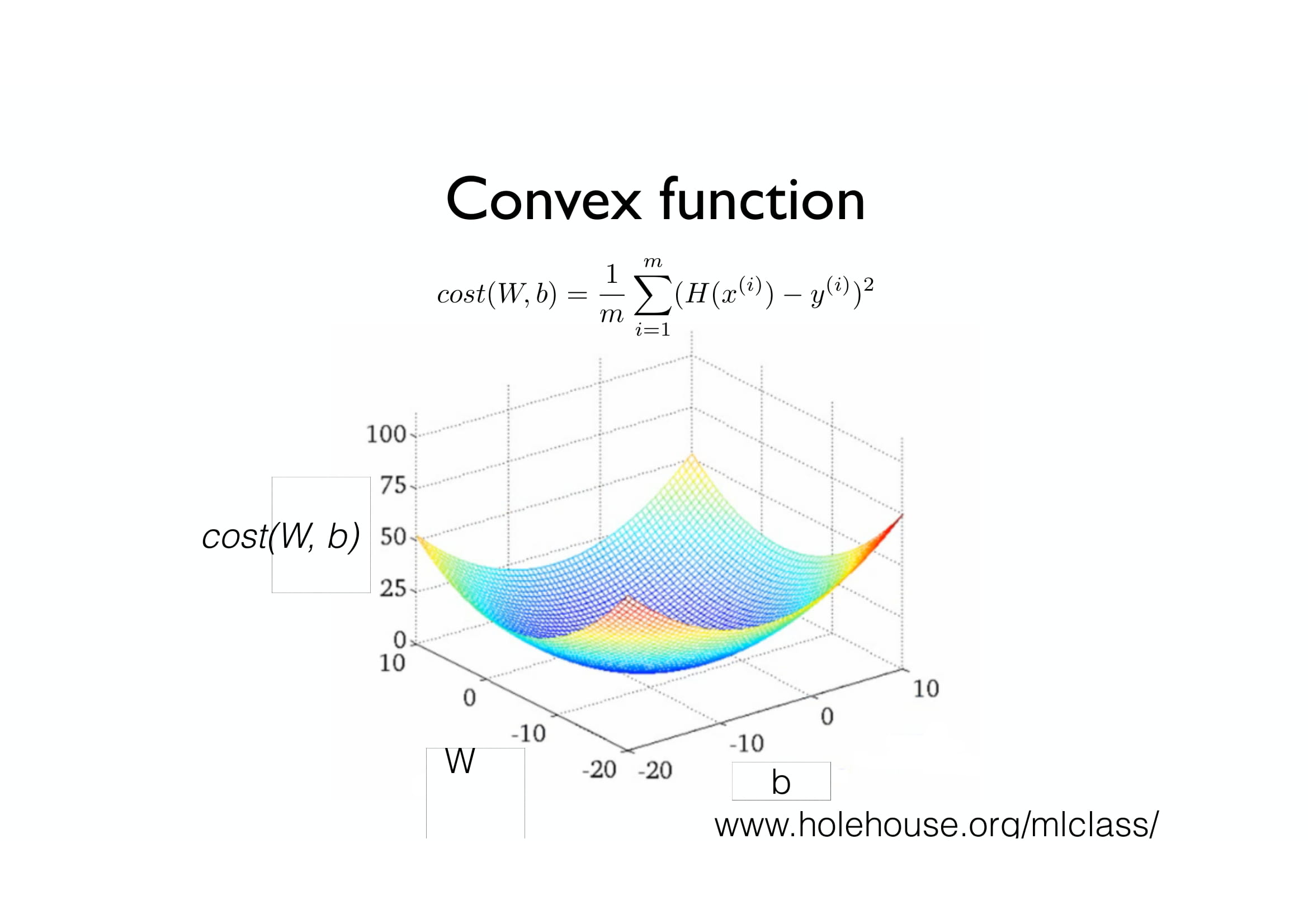
그러므로, 우리는 Cost function을 저렇게 이상하게 생긴 함수로 두면 안되고,
아름다운 밥그릇 모양 (중간이 패인 트램펄린 모양?)으로 생긴 함수를 사용하여야 합니다.
그러면, 결국 Local minima가 한 개뿐이므로 Local Minima가 Global Minima와 같은 것이 됩니다.
이런 식으로, Local minima와 Global minima가 동일한 아름다운 함수를 우리는 Convex function이라고 부릅니다.
그러므로, 우리는 Convex function을 Cost function으로 사용하여야 합니다.

다음 시간에는, Multi-variable Linear Regression(다변수 선형 회귀)에 대해 배워보겠습니다.
(왜 로지스틱이라고 적혀있는지는 잘 모르겠습니다;; 분명 다음엔 Linear regression인데;)
그럼 안녕!
'인공지능 > 모두를 위한 딥러닝 (sung kim) lec' 카테고리의 다른 글
| 모두를 위한 딥러닝 부록편 - 미분의 개념과 Gradient Descent (1) | 2019.05.10 |
|---|---|
| 모두를 위한 딥러닝 (sung kim) lec5 - Logistic Classification (로지스틱 회귀분석) (0) | 2019.05.09 |
| 모두를 위한 딥러닝 (sung kim) lec4 - Multivariable Linear Regression (다변수 선형 회귀) (1) | 2019.04.09 |
| 모두를 위한 딥러닝 (sung kim) lec2 - Linear regression & cost function (0) | 2019.03.30 |
| 모두를 위한 딥러닝 (sung kim) lec1 - 머신 러닝 기초 (0) | 2019.03.28 |
텐서플로우 - Linear regression 코드 정리
- 파이썬을 거의 모르는 사람도, 코드를 이해 가능할만큼, 함수와 기타 등등이 뭔지 정리함.
- 내가 강의할때 보거나 할것.
* 텐서플로우가 어떻게 돌아가는지에 대한 이해는 있어야함!
모르면 머신러닝 포스팅 lab 1&2 보기
import tensorflow as tf'텐서플로우' 라는 패키지를 불러와서, 그 이름을 "tf" 라고 하자.
* as tf 안하면 tensorflow 관련 함수 호출할때 tensorflow.~~~ 해야되는데,
as tf 하면 tf.~~~하면 됨, 아주 간편함!
x_train = [1, 2, 3, 4]
y_train = [0,-1,-2,-3]x,y값을 일단 선언해둠. (데이터를 이걸로 할거라 미리 저장해 놓는 것)
# Placeholder 설정
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
# 변수 설정
W = tf.Variable(tf.random_normal([1]))
b = tf.Variable(tf.random_normal([1]))tf.Placeholder 뜻 : 지금 미리 값을 넣어두는 것이 아니고, 나중에 sess.run 할때 데이터를 집어넣을 것임.
뭔소린지 모르겠다면 머신러닝 포스팅 lab 1&2로 가서 확인할 것.
tf.Variable 뜻 : 텐서플로우의 변수선언.
tf.random_normal([1])) 뜻 : [1] 크기의 랜덤한 (정규분포를 따르는) 수를 생성함.
Linear regression 코드이므로, W,b값이 각각 하나이기 때문에 [1] 씩만 생성함.
hypothesis = X * W + bLinear regression 의 Hypothesis function H(x) = W*x + b 를 hypothesis로 선언함.
cost = tf.reduce_mean(tf.square(hypothesis - Y))Cost function이었던
$$(H(x) - y)^2 을 각각의 데이터 m개에 대하여 모두 더하고, m으로 나누어 평균을 구함.$$
을 구현한 것.
tf.square 뜻 : 제곱.
tf.reduce_mean 뜻 : 평균.
* hypothesis 는 x*W + b이고, x 는 크기 4의 배열이라 계산된 총 크기는 [4],
y도 [4] 이므로 둘이 빼면 그냥 다 더한거랑 똑같은 게 됨.
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)Gradient Descent 방법을 이용하여 train함.
minimize(cost) : cost를 최소화 시킬것임.
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(1001):
sess.run(train, feed_dict={X: x_train, Y: y_train})
if step%50 == 0:
W_val, b_val, cost_val = sess.run([W, b, cost], feed_dict={X: x_train, Y: y_train})
print(" < Step : %d>" %step)
print("Cost : ",cost_val,"\nW :",W_val,"\nb : ",b_val,"\n\n")
# evaluate training accuracy
print(f"W: {W_val} b: {b_val} cost: {cost_val}")session을 열음.
sess.run(tf.global_variables_initializer()) 뜻 : 아직 초기화되지 않은 (값이 박히지도 않은) 변수들을 죄다 초기화해줌.
이거 안하면 변수 터짐.
for step in range(1001) : 뜻 - 0부터 1000까지 돌릴것 ㅎ
sess.run(train, feed_dict = {X: x_train, Y: y_train}) 뜻 : train 함수를 실행시킴 (minimize(cost) 한것)
cost에는 tf.square(Hypothesis - Y) 가 있으니 Y값이 필요할 것이고,
Hypothesis 에는 X*W + b가 있으므로 X값이 필요함.
그 두개의 X,Y를 아까 선언해뒀던 x_train, y_train값으로 집어넣음.
if step%50 == 0: - step이 50의 배수일때 (50,100,150,200 ... , 1000번째 step에서 : )
W_val, b_val, cost_val = sess.run([W, b, cost], feed_dict={X: x_train, Y: y_train}) 뜻 :
W_val, b_val, cost_val 에 각각 W,b,cost의 값을 집어넣음.
cost의 값에는 위에서 언급했듯이 X,Y 둘다 있으므로, feed_dict 로 X,Y값으로 넣어줌.
아래는 간단한 print이므로 설명 생략.
끝~
'인공지능 > 딥러닝 개념 정리노트' 카테고리의 다른 글
| 딥러닝 개념정리 노트 - 머신 러닝 / Supervised learning / Unsupervised learning (0) | 2019.04.02 |
|---|