강화학습
강화학습 강의 (CS234) 8강 - Policy Gradient

- 본 포스팅은 CS234 8강의 내용을 정리합니다.
참고로, 8~10강까지의 내용은 비슷한 내용을 주제로 연강을 하게 됩니다.

이번 시간에는 Policy Search, Policy Gradient에 대해 배워보도록 하겠다.

저번 시간에, 우리는 파라미터 θ에 대해 (w에 대해) value값 및 action-value (Q)을 찾는 방법을 배웠다.
그래서, 그렇게 생성된 value값을 사용하여 직접 policy를 만드는 방식을 사용했다.
(ε-greedy 방식을 사용해서 최대의 value값을 가지는, 또는 랜덤한 policy를 찾는 방법을 사용했던 것을 생각해보자.)
그런데 이번 시간에는, 우리는 policy πθ를 직접 파라미터로 사용할 것이다.
즉, value 값에서 policy를 찾는 것이 아니라, θ (또는 w)의 값을 토대로 policy를 직접 얻을 것이다.
또, 지금까지와 비슷하게 model에 대한 접근 없이, model-free한 RL을 진행하게 될 것이다.

들어가기에 앞서, 사실 reinforcement learning도 policy를 기반으로 할지, value를 기반으로 할지 등에서 조금씩 나뉜다.
Value-Based라고 한다면, ε-greedy와 같은 형식으로 policy를 도출하게 되고,
Policy-Based라면 Value function 없이 직접 policy를 배우게 된다.
Actor-Critic은 그 사이에 있는 놈들인데, 나중에 다루게 될 것이니 일단 넘기도록 하자.

Policy-Based RL이 가지는 장점과 단점들에 대해 살펴보자.
우선, 장점들을 먼저 살펴보자면, Parametrization을 통해 policy를 나타내는 것이 더욱 효율적일 때가 있다. (사실 상황에 따라 다르긴 하다.)
또, high-dimensional / continuous action space의 경우 action-value pair을 사용하는 것 보다 훨씩 효율적이며,
stochastic policy, 즉 무작위적 policy를 가질 수 있게 된다.
value function을 바탕으로 policy를 짜면, 보통 최대의 value값을 갖는 policy를 선택하는데, 이는 stochastic한 policy를 얻지 못하게 막는다.
그런데 왜 stochastic policy가 필요한지는 후술하도록 하겠다.
단점들도 있는데, 우선 대부분의 policy-based RL은 global optima에 수렴하지 않고, local optima에 수렴하는 경우가 많다.
또, 일반적으로 policy를 계산하는 것은 sample inefficient 하다. (sample의 갯수가 많아야 한다는 뜻)

그런데, 아까 전에 stochastic policy를 학습할 수 있는 것이 장점이라고 했는데, 왜 stochastic policy가 필요할까?
가장 간단한 예시로, 가위바위보를 하는 Agent를 만든다고 생각해보도록 하자.
만약 모든 policy가 deterministic 하다면 어떨까?
예를 들어, 처음에는 바위를 내고, 전판에 상대가 보를 냈으면 다음판엔 가위를 내고, ... 하는 식으로 학습되었다고 해보자.
그렇게 학습을 끝낸 후 사람과 가위바위보를 시키면 잘 해낼 수 있을까?
가위바위보를 한판만 하는 거면 모르겠지만, 여러 판 하다 보면 결국 사람이 이게 어떤 메커니즘으로 흘러가는지 알게 되고, 그냥 처음에 보를 내고, 그 다음에 주먹을 내고, ... 하는 식으로 간파가 가능하다.
즉, 가장 최적의 policy는 사실, 가위바위보 셋 중 하나를 랜덤으로 내는 것이다.
아직 잘 와닿지 않는다면, 다음 예시를 통해 조금 더 와닿게 해 보겠다.

위와 같은 grid world가 있다고 하자.
당연히 저기 있는 돈꾸러미가 goal이고, 해골 무늬에 들어가면 죽게 된다.
(해골이나 돈꾸러미에서 시작하는 일은 없다고 가정한다.)
Agent는 동서남북 네 방향만을 관찰할 수 있어서, 동서남북의 칸에 벽이 있나 없나만을 알 수 있다.
또, 자신이 하얀 블럭 위에 있는지 회색 블럭 위에 있는지도 알 수 없다.
자, 이에 따라 돈꾸러미에 들어가는 policy를 짠다면 어떻게 될까?

우선, 하얀색의 블럭 세 개에서의 policy는 자명하게 구할 수 있다.
왼쪽 흰 블럭의 policy를 생각하면 : 왼쪽과 위쪽에 블럭이 있고, 아래쪽에 블럭이 없으면 오른쪽으로 간다! 가 될 것이고,
오른쪽 흰 블럭의 policy를 생각하면 : 오른쪽과 위쪽에 블럭이 있고, 아래쪽에 블럭이 없으면 왼쪽으로 간다! 가 될 것이다.
또, 가운데 흰 블럭은 : 위에만 블럭이 있으니, 아래로 간다! 가 policy가 될 것이다.
이렇게 하면 흰 블럭 위에 있을 때는 최적의 policy가 된다.
문제는 회색 블럭에 있을 때이다.
저 두 블럭에서는 사실 들어오는 feature가 동일하다. "아래, 위에 블럭이 있고, 왼쪽, 오른쪽은 비어 있다" 라는 feature이다.
하지만 저 feature에 대해 어떤 한 가지의 policy를 정할 수 있을까?
만약 "왼쪽으로 간다"라는 policy를 정한다면, 왼쪽 위 흰 블럭 또는 회색 블럭에서 시작하는 경우에는, 영원히 goal에 도달하지 못하게 될 것이다.
반대로 "오른쪽으로 간다"라는 policy를 정한다면, 오른쪽 위 흰 블럭 또는 회색 블럭에서 시작하는 경우에 goal에 영원히 도달하지 못한다.
하지만 Value-based learning같은 경우에는 거의 greedy한 방식으로, deterministic한 policy를 정하게 된다.
이렇게 deterministic한 policy를 정하는 경우, 이처럼 갇히게 되는 경우가 발생하여 좋지 못한 policy가 되고 만다.

그렇다면, 위의 회색 블럭의 policy를 "50% 확률로 왼쪽으로, 50%확률로 오른쪽으로 간다" 라고 잡으면 어떻게 될까?
어디서 시작하더라도, 충분한 시간 뒤에는 결국 goal에 도착하는 이상적인 policy가 완성되게 된다.
이것이 바로 stochastic policy가 필요한 이유이고, 이것이 바로 Value-Based RL이 아닌 Policy-Based RL이 필요한 이유이다.
Value-Based RL같은 경우 위와 같은 Stochastic Policy를 학습하지 못하지만,
Policy-Based RL은 저런 optimal stochastic policy도 할습할 수 있기 때문이다.

이제 본격적으로 policy based RL을 시작해 보도록 하자.
우리의 목표는 최고의 파라미터 θ를 찾아서 parametrized πθ를 찾는 것이다.
그런데, πθ가 얼마나 좋은지 어떻게 알 수 있을까?
우선 episodic environments (H steps 또는 terminal까지)의 경우, J(θ)를 start state의 Value값으로 둘 수 있다.
그리고 continuing environments 같은 경우, πθ의 평균값을 사용하거나, time-step당 reward의 평균을 사용한다.
오늘은 대부분 episodic 한 경우만 다루겠지만, 손쉽게 continuing / infinite horizon인 경우로 연장시킬 수 있다.

그리고 알아둘 점이 하나 있는데, 바로 policy based RL은 "optimization" 문제라는 것이다.
즉, 최대의 Vπθ를 갖는 parameter θ를 구해야 한다는 것이다.
물론 gradient-free한 방식도 사용할 수는 있다. (위 ppt에 나열된 방법)
하지만, 요즘에는 일반적으로 gradient를 사용하는 방식을 자주 사용한다. (강의명도 policy gradient다!)

Gradient-Free 방식을 사용한 예시 중 하나가 바로 위 예시이다.
사람이 걷기 편하게 보조하는 기계를 학습시키는 것인데, 자세한 내용은 다음 유튜브를 참고하기 바란다.
https://www.youtube.com/watch?v=Dkp_xjbRYCo

그리고, 사실 Gradient Free한 방식은 꽤나 잘 먹힌다. 그래서 간단한 baseline으로 자주 사용된다.
어떠한 policy parameterization을 대상으로도 잘 먹히고, 심지어는 미분 불가능한 경우에도 잘 작동하는 방식이다.
또, 병렬화 작업도 매우 쉽게 된다.
하지만, 치명적인 단점이 있는데, 바로 sample-efficient 하지 못하다는 것이다.
즉, 학습하는 데 매우 많은 데이터가 필요하다.

그러니까 Gradient-Free 방식은 이제 저기로 제쳐두고, policy gradient 방식에 대해 알아보자.

그렇다면 Policy Gradient가 그래서 어떻게 작동하는지 설명해보겠다.
우선 V(θ) = Vπθ로 둔다. 그리고 아까 말했다시피, 오늘은 episodic MDP의 경우만을 생각하자.
그러면 Policy Gradient 알고리즘을 사용하여 V(θ)의 local maximum을 찾을 수 있다. (Gradient Descent 사용)
그렇게 θ에 대한 V(θ)의 local maximum을 찾을 때 사용되는 식은 위 ppt에서 볼 수 있다.
이 떄, 언제나 그래왔듯 α는 learning rate이다.

그래서 이제 Gradient 계산을 해야 하는데...
필자는 아직 고등학생인지라 수학에 대해 아직 좀 많이 무지하다.
Finite Difference가 뭔뜻인지 (한정된 차이?는 아니지 않겠는가;;) 인터넷에 검색해 보니까, "유한 차분법" 이라는 방법이라고 한다.
그래서 이번 슬라이드는 완벽하게 이해하지 못했다.
그래도 이해한 것이라도 끄적여보자면,
우선 닫힌 공간 [1, n]의 있는 모든 k에 대하여, θ에 대한 k의 편미분을 계산한다.
그리고 그 편미분 값을 조금 바꿔서(약간 증가시키거나 감소시킨다는 얘기인가?) 실제 미분값에 근사시킨다.
그 뒤, n dimension을 따라 n번 evaluate해서 policy gradient를 계산한다.
이 방식은 간단(??)하지만, 약간 노이즈가 있고 inefficient한 방식이다. 하지만, 가끔 효율적으로 사용되는데,
미분 불가능한 policy를 포함해 어떠한 policy에도 작동할 수 있기 때문이다.

이 방식을 사용하여, 로봇 AIBO를 걷게 시킨 실험도 있다. (2004년)

어떻게 parameterization을 했는가 보니,
state를 두지 않고, 위 슬라이드에 나온 대로 parameterization을 진행하여, 각각의 파라미터에서 랜덤으로 -ε, 0, ε 셋 중 하나를 더해 policy를 얻었다고 한다.

그런데 위에서 이거 2004년에 했다고 했는데, 이걸 어떻게 computational effecient 하게 진행했냐면,
우선 로봇 3개를 한번에 구동한다.
그리고 각각 iteration마다 policy 15개를 evaluate한다.
그리고, 각각의 policy도 3번씩 evaluate하고 (noise를 줄이려고) 그것의 평균을 구한다.
이렇게 했더니, 각 iteration이 7.5분 안에 끝났다고 한다.
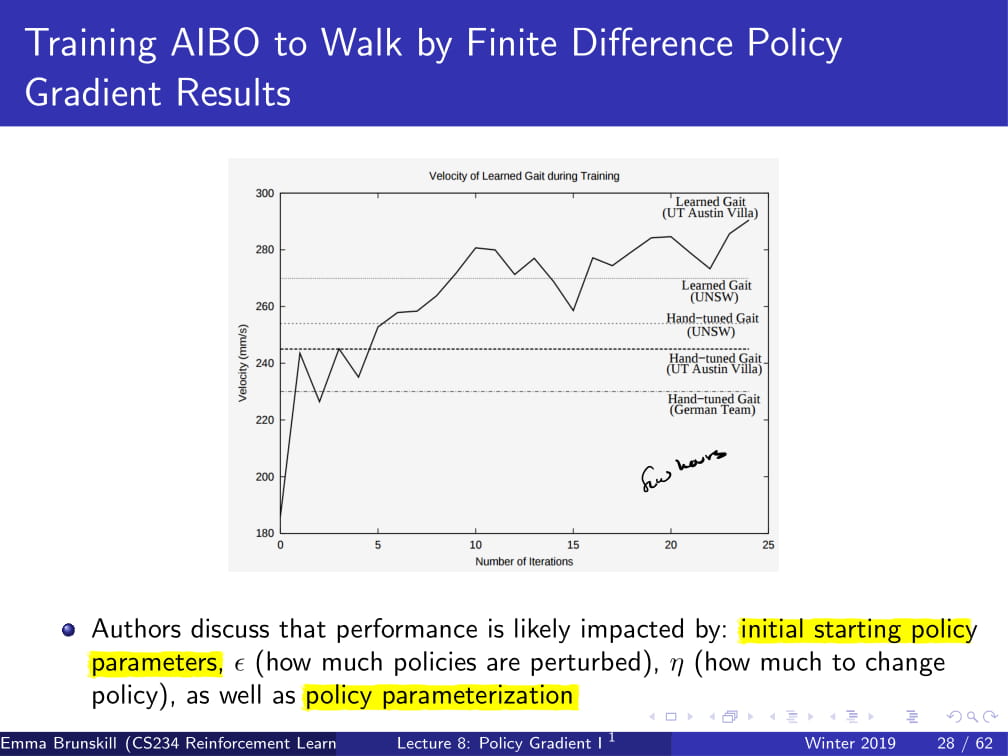
그렇게 traning 시켰더니, 꽤 잘 하는 모습을 보여줬다고 한다.
그리고 이 AIBO의 성능은 초기 starting policy parameter, ε (더하고 빼지던 정도), α (learning rate), 그리고 policy parameterization 등이 영향을 미쳤다고 한다.

그리고, 이번에는 방금의 Finite Difference 방식이 아니라 그냥 analytical 하게 gradient를 구하는 방법을 알아보자.
당연하게도, 이 방식을 사용하려면 policy πθ가 미분 가능해야 하고, gradient를 알고있다고 가정해야 한다.
(즉, 이것 자체가 연산 가능하다는 것을 알고 있어야 한다는 것이다.)

그리고 이 방식을 사용할 때는, likelihood ratio policy라는 것을 사용한다.
우선, 이 방식은 Episodic 한 방식에서만 사용되며, 예전부터 해왔듯이 trajectory를 설정한다.
(당연히 episodic이므로 마지막에 Terminal이 있어야 한다.)
그리고, Reward function R은 그냥 trajectory의 reward값의 평균이다.
또한, 이렇게 두면 Policy value는 해당 policy를 따랐을 때의 Reward값의 평균이 되는데, 이를 다시 쓰면 해당 episode에서, 즉 trajectory를 따라갈 때 얻는 Reward R과 확률 P의 곱의 평균이다.
(policy에서 확률이 왜 나오냐 할 수도 있겠지만, 이제는 이것이 deterministic하지 않는다는 것을 알아야 한다!)
그리고, 이제부터 나오는 대부분의 수식들에는 Reward Function이 그대로 쓰이기 보단, 위의 형태와 같이 Probability P와 R의 곱 형태로 나오게 될 것이다.

그리고 이 상태에서, 위 V(θ)의 Policy Gradient를 구하면 (θ에 대해 Gradient한다), 위와 같게 된다.
딱히 설명할 필요는 없겠지만 대충이라도 설명을 해 보자면,
첫 번째 줄에는 그냥 양변에 gradient를 씌워 준 것이고, (이 표현이 맞는지는 모르겠지만... 뭔뜻인지 알겠지??)
어차피 θ를 인수로 갖는 것은 P(𝛾;θ) 뿐이니 저 시그마 안으로 들어가 준 다음에,
P(𝛾;θ)/P(𝛾;θ) 를 곱해준다. (1을 곱한 것과 같다.)
그리고, P(𝛾;θ)를 분수 아래로, ∇θP(𝛾;θ)를 분수 위로 올리면, P(𝛾;θ)R(𝛾) * ∇θP(𝛾;θ)/P(𝛾;θ)가 된다.
그런데, ∇θlog(P(𝛾;θ)) 는 1/P(𝛾;θ) * ∇θP(𝛾;θ)라고 한다.(왠지는 필자도 잘 모르겠다 ㅠㅠㅠ)
그래서 이를 정리하면, 맨 아래 식이 나온다.
이 식을 사용하는 이유는, policy를 사용하여 trajectory 몇 개를 sampling 한 뒤에, reward를 조금 구하면서 Gradient를 구할 수 있기 때문이다.
즉, 어떻게 Gradient를 구해야 할지에 대한 방법을 얻게 된 것이다.

어떻게 Gradient를 구하는지 조금만 더 자세히 보자면,
우리의 목적은 policy parameters θ를 찾는 것이므로,
θ에 대해 Gradient를 아까 위에서 한 것처럼 구한 뒤에,
그 값을 그냥 policy 몇 번 돌려서 구한 값과 유사한 값으로 맞춰주면 되는 것이다.

...그런데 우리가 지금 뭘 하고 있는걸까?
그냥 일반적으로 Gradient Descent를 사용하는 다른 알고리즘을 생각하면 편하다.
우리는 지금, Gradient를 구하는 방법을 알게 되었다.
그런데 우리의 trajectory는 Policy Parameter θ에 따라 달라지지 않겠는가!
그러므로, 현재 parameter가 가지는 reward값이 가장 커지도록 parameter값을 바꿔준다고 생각하면 된다.
조금 더 자세히 하자면, 그 sample이 얼마나 좋은지에 비례해서 그 sample이 나오게 만드는 확률을 높여주는 방향으로 진행된다.
현재 trajectory의 state에서 앞으로 가는 것이 가장 reward가 높은 행동이라면, 앞으로 가는 확률(로그가 씌워져 있긴 하지만)을 높이는 방향으로 parameter를 움직인다.

조금 더 직관적으로, 위 그래프를 보자.
f(x)는 Reward Function이고, P(x)는 trajectory이다.
그래서, 좋은 reward를 갖는 trajectory를 갖게 parameter를 조정하게 된다. (위 예시에서는, 아마 가장 오른쪽의 값이 가장 reward가 높은이다.)
그냥 이게 다다. 매우 직관적이지 않은가?

이제 우리가 할 것은, 위 Trajectory를 State와 Action에 대한 식으로 풀어 쓰는 것이다.
일단 위 식에서 Trajectory를 갖는 ∇θlogP(𝛾⁽i⁾;θ) 를 보면, parameter θ를 가질 때, i번째 trajectory의 Log Probaility의 미분값이다.
그런 일단, P(𝛾⁽i⁾;θ) 이 부분만 위의 식 μ(s₀)𝚷πθ(at|st)P(st+1|st, at) 라고 나타낼 수 있다.
왠지 대충만 설명하자면, 결국 P(𝛾⁽i⁾;θ)의 의미는 i번째 trajectory의 Prob을 의미하는데,
현재 policy에서 state가 주어졌을 때 action이 나올 확률에 dynamics model P를 곱해준 뒤에, initial state distribution까지 곱해주면, 결국 같은 것을 의미하는 식이 되는 것이다.
그리고 로그를 다시 안쪽으로 넣어주면, product pi 는 sigma가 되어 이와 같이 쓰일 수 있고,
그런데 이를 또다시 θ에 대해 미분해 주면, 신비로운 일이 잇어난다.
우선 왼쪽의 logμ(s₀)는 θ와 독립적이므로, θ에 대한 편미분을 하면 0이 된다.
오른쪽의 P(st+1|st, at) 또한 θ와 독립적이므로, θ에 대한 편미분값은 0이다.
그러면 결국엔 θ를 갖는 식 하나, 가운데 log(πθ(at|st))만 θ에 대해 편미분해주면 되는, 간단한 현상이 일어난다.
그래서 결국 마지막 식이 도출되게 된다.
근데 우리가 왜 이 짓을 했을까?
첫 번째 식과 마지막 결과식을 비교해 보자.
첫 번째 식에는 trajectory가 포함되어 있으므로, dynamics model이 무조건 필요하게 된다.
그런데, 이렇게 trajectory를 state와 action에 대한 식으로 바꿔 주니, dynamics model이 더 이상 필요하지 않다.
그냥 단순한 policy의 logprob값의 편미분값으로만 위 식이 표현이 되는 것이다!

그리고 우리는 위 식을, Score Function이라고 부르게 된다.

이제 지금까지 나온 내용을 다시 뭉쳐보자면 위와 같다.
우리는 좋은 parameter θ를 찾고자 한 것이다.
그리고, V(θ)의 편미분값은 사실 위 (1/m)Σ(i=1 ~ m)R(𝛾(i))∇θlog(P(𝛾(i); θ))이다.
또, 아까 전에 저 P(𝛾(i); θ)을 풀어 쓴 대로 써보면, (1/m)Σ(i=1 ~ m)R(𝛾(i))∇θlog(πθ(at|st))가 된다!
위 식을 조금만 풀어서 쓰자면, trajectory를 m번씩 돌 때, 각각의 trajectory에서 나온 Reward값의 평균에다가,
∇θlog(πθ(at|st))를 곱한 식이 된다.
즉, ∇θlog(πθ(at|st))를 score function으로 갖는 함수가 완성된다. (reward에다가 저 값들만 곱하면 Value값이므로)
또한, 이것도 마찬가지로 dynamics model이 필요없는, 매우 간결한 식이 된다.

그리고, 이 Policy Gradient Theorm은 뒤 식을 약간 일반화 시킨 식이다.
policy objective function J를 J1(episodic reward), JavR(time step당 평균 reward), 1/1-𝛾 * JavV(평균 value)라고 한다면
다음과 같은 식이 써진다. (위 ppt 참조 ㅎㅎ)

그런데, 위와 같은 식은 unbiased하긴 하지만 매우 noisy하다.
대충 딱 보면 monte Carlo 방식이 떠오르지 않는가?
사실상 trajectory의 episodic reward라던지, trajectory의 평균 reward를 갖고 계산한다는 점이 말이다.
그래서, 이러한, 매우 noisy하다는 문제점을 해결하기 위해 여러 가지 방법을 사용한다.
오늘은, Temporal structure과 Baseline에 대해 알아보고, 다음 시간에 추가적인 테크닉들을 설명하겠다.

우선, Temporal Structure는, 말 그대로 우리 model에게 "지금 우리가 하고 있는 것은 temporal 한, 즉 시간적 구조가 나타나는 일이란다" 하고 알려주는 것이다.
이것을 하기 위해서, 위와 같은 공식들이 유도된다.
한번 쭉 읽어보면 딱히 필자가 유도하지 않더라도 어느 정도는 다 이해할 것이라 믿고 넘기겠다.
...사실 필자가 이해하지를 못하겠다 ㅠㅠㅠ
혹시라도 필자를 이해시켜줄 수 있는 용자가 있다면, 댓글로 조언 부탁바란다 ㅠ
(사실 이 강의 설명이 이렇게까지 늦은 이유도, 수식들 하나하나 다 이해하면서 넘어가느라 그랬는데, 여기서부턴 도저시 모르겠다 ㅠㅠ)
다만, 마지막 줄에서 logπθ(at, st)는 logπθ(at|st)의 오타인 것 같다.




위 내용들은 나--중에, 필자가 저 수식들을 이해할 정도의 실력이 되면 그때 다시한번 도전해 보도록 하고,
다음 시간엔 Policy search에 대한 더 많은 이야기들을 해 보도록 하겠다.
그럼... 좀 씁쓸하긴 하지만...
안녕!
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 7강 - Imitation Learning / Inverse RL (1) | 2019.08.26 |
|---|---|
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
강화학습 강의 (CS234) 5강 - Value Function Approximation

- 본 포스팅은 CS234 5강의 내용을 정리합니다.
* 기본적인 Neural Network 및 머신러닝 지식이 있으면 이해가 훨씬 빠릅니다! (그냥 알고 있어야 이해가 될것 같습니다 ㅎㅎ)

이번 강의에선 Value Function Approximation, 줄여서 VFA에 대해서 배운다.
주로 다룰 내용은 위 목차의 2번이 되겠다.
(3번은 시간 문제상 대부분 생략된다. 어뜨케 1강에서 5강까지 죄다 후반내용은 생략하시네 교수님;;)

지난 시간에, (CS234 4강의 내용) 경험을 토대로 좋은 policy를 얻는 방법을 배웠었다.
SARSA, Q-Learning, Monte Carlo, TD 등등...
그런데, 지금까지 이런 내용들을 배울 땐 value function이나 state-action value function을 벡터나 매트릭스 형태로 나타낼 수 있다는 가정 하에 배웠었다.
(이를 Tabular representation이라고 한다.)
그러나, 실제로는 value function이 그렇게 돼 있는 경우는 흔치 않다.
가령 자율운전 자동차를 만든다고 할 때, state가 얼마나 많겠는가?
왼쪽으로 1도 갔을 때, 2도 갔을 때.... 180도 갔을 때 등등만 하더라도 그렇겠지만,
거기다가 속도나 주변 차들의 유무 등등 수없이 많은 state들이 존재하게 될 것이다.
그렇기 때문에, 벡터나 매트릭스로 value function을 나타내는 tabular representation은 강화 학습의 실제 적용에 부족한 점이 있다.

이를 해결하기 위해서, 1강에 배웠던 Generalization을 사용하게 될 것이다.
이걸 왜쓰냐고? 일단 계속 보자.

Value Function Approximation이란, Value function을 state, action을 parameter로 갖는 function으로 만드는 것이다.
위의 사진을 보면 이해가 쉬울 듯 하다.
(V와 Q 위에 있는 건 hat이라고 하고, 예측값을 의미한다.)
Neural Network를 배우고 온 사람들이라면 이해가 쉬울 것이라 생각한다.
state, action s,a와 weight vector W를 이용해서 V,Q값을 계산하는 것이므로...
Neural Network와 상당히 비슷한 모습을 보인다.

이 짓 (VFA) 를 하는 이유는...
모든 state에서 Dynamics, Value, Q, Policy들을 명시적으로 알 필요 없이,
state와 state, function 을 모두 아우르는 간단한 일반항을 만들기 위함이다.
가령, V(s,w) 함수를 제대로 만들어 놨다면, 어떤 state에서도 그냥 저 V(s,w)에 s값만 대입하면 value가 그대로 튀어나온다.
즉, w 벡터 하나만 있으면 어떤 상황에서도 value가 그냥 나온다!

이렇게 Generalization을 하면 좋은 점은,
(P,R) / V / Q / π를 저장하는데 메모리가 덜 들고,
(P,R) / V / Q / π를 계산하는데 연산이 덜 필요하며,
좋은 (P,R) / V / Q / π를 찾을 때 experience가 줄어든다.
* 여기서 experience란 좋은 (P,R) / V / Q / π를 찾는 데 필요한 데이터의 수를 의미한다.
주의할 점은, 필요한 data의 수가 줄어든다고 하더라도 적은 데이터만을 갖고 VFA를 하게 되면, 좋지 못한 approximation이 될 수 있다는 것이다.
Neural network와 굉장히 유사한 느낌이라고 보면 될듯 하다.
데이터가 적게 들어와도 fitting을 잘 할 수 있겠지만 그렇다고 그게 실제 data에 잘 적용 가능한 approximation이 아닌것 처럼 말이다.
또한, 위와 비슷한 이유로 VFA를 사용하면 메모리 / 연산 횟수 / 데이터 갯수는 줄어들겠으나, representational capacity도 같이 줄어들게 된다.
*representational capacity는 머신러닝 모델의 flexibility, 즉 실제 데이터의 적응력 정도를 의미함.

그러면 VFA에 사용할 approximator에는 어떤 것들이 있을까?
Linear approximator를 사용할 수도 있고,
Neural Network를 사용할 수도 있고, Decision tree를 사용할 수도 있다.
이는 머신러닝 모델을 선택하는 것과 비슷한 맥락으로 볼 수도 있을 것 같다.
이 중에서 오늘은 Linear feature representation을 다룰 것이다.
(다음 시간에 Neural network도 다룬다.)

여기서 Gradient Descent에 대한 설명이 나오는데, 여기다가 다시 Gradient Descent를 설명하긴 좀 그렇고 하니 이미 아는 사람은 그냥 넘어가고, 모르면 다음 링크를 타고 들어가서 확인해보자.
https://cding.tistory.com/21?category=704767 - Gradient Descent
https://cding.tistory.com/56?category=704767 - 미분과 Gradient Descent에 대한 이해
왜 다 내 블로그 링크냐고?
아니 뭐 그럼 다른데 가서 보등가 ㅎㅎ...

일단 본격적인 VFA에 들어가기 앞서, 일단 쉬운 버전 먼저 시작해보자.
어떤 state s에 대해서든 완벽한 진짜 Value 값을 던져주는 오라클이라는 존재가 있다고 가정하자.
그리고 그 데이터들을 바탕으로, state s에 대해 value를 찾는 function을 구하려고 한다.
즉 state s가 주어졌을 때 value 값을 찾아내는 w의 값을 찾아내고 싶다는 것이다.

이렇게 하면, Supervised learning하는 과정과 거의 동일해진다.
오라클이 던져준 실제 V값과 우리가 구하고 싶은 Value function을 갖고 Gradient Descent 알고리즘을 적용하면 최적의Value function이 나올테니 말이다.
여기서 잠깐 Stochastic Gradient Descent (SGD)에 대한 설명이 나온다.
그냥 Gradient Descent 알고리즘은 모든 데이터의 cost값들과 미분값들을 토대로 w값을 update해 주었다면,
SGD는 모든 데이터가 아니라 랜덤하게 몇개의 데이터의 cost값들과 미분값들만을 가지고 w값을 update한다.
이렇게 하면 한번 update할 때 시간도 덜 걸리고, 일단 Gradient Descent와 거의 유사한 결과를 낼 수 있다.
근데 갑자기 이걸 왜 알려주냐고?
솔직히 나도 모르겠다 ㅎㅎ;

그런데 실제로 우리가 오라클이라는 존재를 알고 있진 않다.
즉, 실제 Value값을 알려주는 존재같은건 없다는 것이다.
이런 상황에서, 우리는 지금처럼과 같이 model에 의존하지 않고 model-free한 VFA를 만들 방법을 강구해야 한다.

그런데 Model-free.. model.... free...?
이거 우리 한번 하지 않았나?
맞다. CS234 3강의 내용이 바로 Model-free policy evaluation이었다!
그 때 우리는 Monte Carlo methods와 Temporal Difference methods, 줄여서 TD methods를 배웠었다.
이 방법을 그대로 VFA에 가져와서, update 과정에서 function approximator을 fitting하는 과정만 추가해서 사용하면 어떨까?
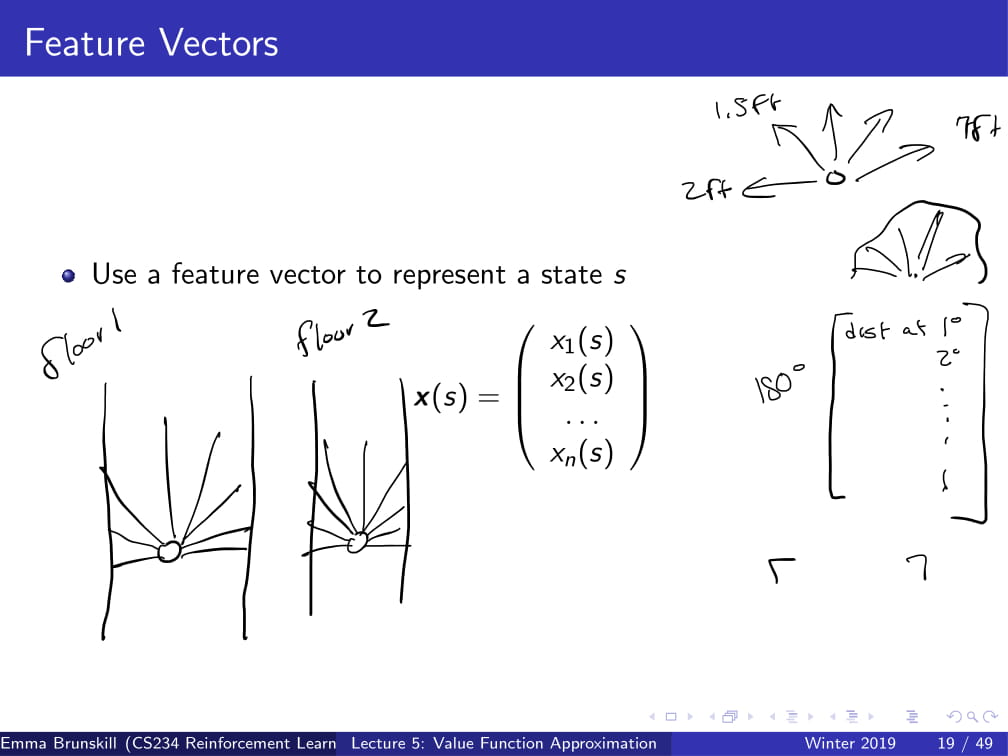
일단 들어가기 앞서 Feature vector이 뭔지 먼저 정의하고 넘어가겠다.
..라고 해도 그냥 별거 없다. 각각의 state에 대한 정보를 담고 있는 vector라는 뜻이다.
자동으로 청소를 해주는 로봇청소기를 예로 들어보자.
만약 이 로봇청소기에 왼쪽부터 오른쪽까지 전방 180도에 대한 거리를 알려주는 센서가 달려있다고 해보자.
그렇다면, 이 로봇청소기의 feature vector은 1도에서 180도까지의 거리가 될 것이다.
x1(s)에는 1도까지의 거리, x2(s)에는 2도까지의 거리 .... 처럼 말이다.
그리고 이것을 x(s)라고 정의해 두도록 하겠다.

그런데 일단, 오라클을 다시 데려와서 Value 값을 알려달라고 해보자.
그러면 위처럼 Value function의 approximation을 구할 수 있게 된다.
위의 내용이 대충 어떤 내용이냐면,
(대충 x(s)값을 사용해서 Supervised learning과 비슷하게 흘러간다고 설명하는 말)
자, 이제 이해했길 바란다.
절대 설명하기 귀찮아서 저렇게 둔 것이 아니다.

그런데 아까도 말했다시피, 우리한테는 오라클 같은건 없다.
그러니, 저번에 배웠던 Monte Carlo 방식을 사용해보자.
Monte Carlo 방식에서 return Gt는 unbiased, noisy한 Value 값이었다.
그리고, Monte Carlo는 지금까지의 경험을 그대로 Gt를 내놓는다.
즉, 이 Gt값은 어떤 state에 대한 true discounted Value 값이 된다.
(그러니까 이 Gt는 경험했던 state에 대해서만큼은 오라클이 던져주는 Value값과 동일한 실제 Value값이다.)
이를 사용하면, 아까 전에 했던 supervised learning과 동일한 방식으로 VFA를 적용할 수 있다.
(수식은 위 수식 참고)

위는 Monte Carlo 방식을 사용한 VFA가 어떻게 작동하는지 잘 알려준다.
사실 이건 딱히 말할 게 없다. 위에 너무 잘 적혀있으니 그냥 위 ppt를 보고 알아가도록 하고, 자세한건 나중에 나올 예시로 짚어보도록 할 것이다.
그래도 대충 설명을 하자면,
(대충 원래 MC에서 weight update가 추가된 것 뿐이라는 내용)
참고로 알아둘 사항만 적어두자면,
Line 5 : First-visit이라고 적혀있긴 하지만, Every-visit MC에도 동일하게 적용가능하다.
Line 7 : X(s)는 아까 했던 feature vector이다.

그럼 직접 예제로 알아보도록 하자.
위 그림 (s1, s2, s3 ... s7)을 통해서 봤을 때,
저 원 안의 수식은 각 state의 feature vector의 계산식을 의미한다.
w 값의 초기화를 [1 1 1 1 1 1 1 1]이라고 하면,
State s1의 feature vector는 [2 0 0 0 0 0 0 1],
State s2의 feature vector는 [0 2 0 0 0 0 0 1],
....
State s7의 feature vector는 [0 0 0 0 0 0 1 2] 가 된다.
action은 a1, a2 두가지가 있는데,
a1은 그림에서 실선으로 표시되며, 무조건 Deterministic하게 s7으로 가게 되고,
a2는 그림에서 점선으로 표시되며, 각각 1/6의 확률로 s1, s2, s3, ... , s6로 가게 된다.
또한, 어떤 state, 어떤 action에도 reward는 0이다.
그리고 우리는 이 상황을 Monte Carlo 방식을 사용해서 w의 값을 update하고 싶은데,
모두 알다시피 Monte Carlo 방식은 무조건 episodic한, 즉 termination이 존재하는 경우에만 사용이 가능하기 때문에
s7에서 a1을 취하면 0.999의 확률로 s7으로 가고, 0.001의 확률로 terminate가 된다고 가정하고 시작할 것이다.
이 때, 우리에게 다음과 같은 episode가 주어졌다고 가정해보자 :
s1, a1, 0, s7, a1, 0, s7, a1, 0, terminate
(State, Action, Reward 쌍이다.)
α = 0.5라고 할 때, w의 값은 어떻게 update되는가?
우선 state s1에서 return 값 G는 무엇인가?
모든 reward가 0이므로, return G도 0이 될 것이다.
그렇다면 s1의 value function의 초기값은 무엇이 될까?
w를 모두 1로 초기화한다고 했고,
s1의 feature vector( x(s1) )가 [2 0 0 0 0 0 0 1] 이었으므로
1*2 + 1*0 + 1*0 + ... + 1*1 = 3이 된다.
이쯤에서 아까 저 위에서 w값을 update하는 방식을 가져오면,
w = w + α(G(s) - V(s, a)) * x(s)
였으므로, 위에서 구한 값들을 여기에 대입하면
w = [1 1 1 1 1 1 1 1] + 0.5(0 - 3) * [2 0 0 0 0 0 0 1]
= [1 1 1 1 1 1 1 1] + -1.5 * [2 0 0 0 0 0 0 1]
= [1 1 1 1 1 1 1 1] + [-3 0 0 0 0 0 0 -1.5]
= [-2 1 1 1 1 1 1 -0.5]
...이렇게 w값이 update가 된다.
다른 episode들로도 한번 연습해 봐도 좋을 듯 하다.


위 두 슬라이드는 Linear VFA가 Converge하는가를 다루는 내용인데, 본인이 이해를 잘 못한 관계로 설명은 생략 ㅎㅎ...
강의 안볼거면 그냥 SGD를 사용하면 Linear VFA는 Linear이 할수 있는 최선으로 fitting된다는 정도로만 알아두자..
(물론 거의 무한하게 계속계속 update할 경우에 그렇게 된다는 거다..)

그런데 방금 전의 예시처럼 episode가 하나하나씩 들어오는 것들을 갖고 w를 update해도 되기야 하겠지만,
만약 episode들의 데이터가 있으면 그냥 그거 그대로 쭉 쓰면 안될까?
그러니까, episode를 하나하나씩 진행시키면서 update하지 말고 한방에 데이터들을 갖고 update할 수 있지 않을까?
...있으니까 말했겠지 뭐!
이를 Batch Monte Carlo Value Function Approximation이라고 부른다.
이름이 너무 길긴 하다..
이건 그냥 Linear Regression에 적용하듯, Analytic하게 적용이 가능하다.
위의 수식만 봐도 대충 이해 가능할 듯 하다.

Monte Carlo 방식은 여기까지만 알아보도록 하고,
이제 TD learning 방식으로 넘어가도록 하자.
일단 저번 저번 시간에 배웠던 TD learning을 잠깐 살펴 보자면,
TD learning은 DP 방식에서 사용하던 bootstrapping을 사용하며 MC 방식에서 사용한 sampling 방식도 사용했었다.

일단 본격적으로 들어가기 앞서, 지금까지 배운 세 가지 approximation을 생각보자.
1. (지금 하고 있는) function approximation
2. bootstrapping (DP / TD)
3. sampling (MC / TD)
그런데 지금 이 세개 모두 다 on-policy라는 것을 쉽사리 알 수 있을 것이다.
결국 지금 갖고 있는 데이터를 바탕으로 가는 것이니 말이다.
그러면, 결국 이 모든 것이 전부 supervised learning과 크게 다르지 않게 된다.
그렇다는 것은, 우리가 하고 있는 대부분의 것들 (위에 세가지) 는 convergence의 문제에서 어느 정도 자유로울 수 있다는 것이다. (거의 항상 수렴한다는 뜻)
그런데 이걸 왜 말해주냐고?
수렴하는지 안하는지 물어보지 말라고 하는 거 아닐까?

이제 본격적으로 들어가서,
원래 TD의 target (sampling)은 r + 𝛾Vπ(s') 이었다면,
VFA에서의 target은 r + 𝛾Vπ(s', w) (V위에 hat은 마음의 눈으로 보자 ㅎ)가 된다.
즉, w값도 찾아야 한다, 이말이다.
아무튼 이렇게 J(w)의 값을 최소화시키는 w값을 찾아가는 것이 바로 TDVFA이다. (길게 쓰기 싫어서 줄여씀)

그냥 위 식을 막 바꾸다 보면 아래까지로 바꿀 수 있다는 뜻 ㅎ
이건 TD때 비슷하게 했으니 그냥 넘기겠읍니다 ^^7

그리고 이를 의사코드로 바꾸면 위처럼 쓸 수 있다.
아까 전의 ppt 내용과 동일하다는 것을 알 수 있다. (거의)

아까 전의 그 예제로 돌아가보도록 하자.
기억이 안난다고?
예제 설명한거 복사해서 메모장에 붙여넣고 해보도록 하자 ㅎ
뭐 아무튼, 그 상황에서 MC 대신 TD learning을 적용해보자.
(참고로, 이번 상황에선 MC가 아닌 TD를 사용하므로, 0.999 어쩌구 하는 부분은 걸러도 된다. episodic 하지 않아도 되니깐 ㅎ)
episode는 [s1, a1, 0, s7]이라고 가정하고, 𝛾=0.9라고 하자.
그러면, w의 update는 어떻게 될까?
위의 수식을 그대로 빼다 박으면,
Δw = 0.5 * (0 + 0.9 * ([0 0 0 0 0 0 1 2] T [1 1 1 1 1 1 1 1]) - [1 0 0 0 0 0 0 2] T [1 1 1 1 1 1 1 1]) * [1 0 0 0 0 0 0 2]
= 0.5 * (2.7 - 3) * [1 0 0 0 0 0 0 2]
= 0.5 * -0.3 * [1 0 0 0 0 0 0 2]
= [-0.15 0 0 0 0 0 0 -0.3]
그리고 이 Δw를 w에다가 더하면,
w = [0.85 1 1 1 1 1 1 0.7]
이런 식으로 바뀌는 것이다.

TD에서도 특정 값에 수렴하는 성질이 있다.
여기두 본인이 이해가 잘 안되는 관계로 생략 ㅎ..
참고로 짤막하게 지나가지만, TD가 MC보다 조금 더 좋은 성적을 내는 경향이 있다.
(그냥 조금 더 좋다)

이제 Control 부분을 다뤄 보도록 하자.
일단 들어가기 앞서서, Function approximation / Bootstrapping / Off-policy learning 을 한번에 적용하려 하면 불안정해질 수도 있다.
그러니까, converge가 안 될 수도 있고, 잘 될 수도 있다는 것이다.

그리고 Control을 할 때, 우리는 Q function을 사용할 것이다. (Action-Value 쌍)
일단 오라클이라는 존재가 우리에게 답을 알려준다면, 어떻게 하면 될까?
아까 전까지 했던 것과 거의 똑같이 하면 된다.
실제 Q값에서 Q의 예측값을 빼서, w값을 최소화시켜주면 되는 것이다.
(위에서는 SGD를 사용한다.)

오라클이 없다면?
아까처럼 feature vector을 만들어야 한다는 점은 동일하지만,
x(s) = [x1(s), x2(s) ... ] 가 아니라, state-action 쌍을 이루도록
x(s, a) = [x1(s, a), x2(s, a) ... ] 로 만들어 둔다.
그 외의 나머지 부분도 아까 전과 동일하다.

그리고 위의 내용들도 아까 전에 했던 것과 4강때 했던 것과 배우 비슷하다.
단지 Return값 Gt와 target이 Q와 관련된 식으로 변화하였고,
function approximator을 추가해줬을 뿐이다.
이쯤에서 5강 내용은 마치도록 하겠다.
본인이 이해를 못한 부분이 꽤 있어서, 이 뒤 부분은 사실 설명을 잘 할 자신이 없다.
나중에 다시 한번 정리하면서 수정할 날이 오면, 더 보충설명을 진행하도록 하겠다.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 7강 - Imitation Learning / Inverse RL (1) | 2019.08.26 |
|---|---|
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |
강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning

- 본 포스팅은 CS234 4강의 내용을 정리합니다.

이번 강의에선,
- Generalized Policy Iteration
- Importance of Exploration
- Monte Carlo Control
- Temporal Difference (TD) Methods for Control
- Maximization Bias
등에 대해 배운다.

On-policy learning이란 직접 경험한 내용을 바탕으로 policy를 예측하고, 개선해 나가는 과정이다.
즉, Agent가 직접 행한 내용에 대해서만 학습을 하는 것이다.
Off-policy learning은 그와 달리 이미 알고 있는 내용들을 바탕으로 아직 실행하지 않은 내용까지 예측해서 policy를 개선해 나가는 것이다.
가령, 다음과 같은 state와 action에 대한 policy를 생각해보자:
s1, a1, s1, a1
s1, a2, s1, a2
off-policy learning의 경우엔 위의 두 가지 policy를 조합하여
s1, a1, s1, a2
의 policy도 수행할 수 있게 된다.

이제 Policy Iteration이 뭔지 다시 한번 불러와 보자.
Policy Iteration이 뭐였느냐 한다면...
우선 Vπ를 계산해 준 다음,
그 값과 Reward model R, dynamics P를 바탕으로 policy를 개선해 나가는 과정이었다.
(자세한 내용은 2강에서 확인하도록 하자.)
그런데, Policy Iteration의 경우엔, 정확한 Reward model과 dynamics(~~가 일어날 확률)가 필요했다.
그래서 저번 강의에서는 model-free policy evaluation에 대해 설명했었는데,
이걸 한번 Policy Iteration에 써먹어 보도록 하자.

그래서 나온 것이 Model Free Policy Iteration이다.
아이디어는 그냥 Reward model과 dynamics를 Q function으로 합쳐버려서
Qπ를 계산하고 이 π를 개선해 나가면 되지 않을까? 하는 생각인 것이다.

이번엔 Monte Carlo for On Policy Q Evaluation에 대해 알아보자.
이는 저번에 배웠던 Monte Carlo for on policy value evaluation과 매우 유사한데,
원래 value evaluation에서는 N(s), G(s)를 썼지만,
Q Evaluation에서는 N(s, a) 와 G(s, a)를 사용한다.
(사실 어느 정도 당연한 이야기인데... Q는 state뿐만 아니라 action 또한 사용하는 function이기 때문이다.)
즉, 원래는 State만을 사용하던 것에서 벗어나서, State, action 쌍을 사용하는 것이다.

이 방식으로, Policy Improvement를 더욱 간단히 만들 수 있다.
그냥 Qπ(s, a)의 argmax를 취하면 그게 다음 policy가 되는 것이다.

그리고 이 방식을 사용하면 Policy Iteration을 매우 간단하게, 그리고 Model-free하게 만들 수 있다.
하지만, 아직 신경써야 할 부분이 있다. 바로 Qπ를 compute하는 부분이다.
만약 policy가 Deterministic 할 때는 policy 안에 특정 action이 존재하지 않는다면, 그 action에 대한 Q function은 절대로 계산하지 못한다.
(결국엔 Deterministic 하다면 policy에 있는 action만 따라가니깐..)

이를 해결하고 model-free한 Qπ를 계산하기 위하여, Exploration을 해야 한다!

이 때 사용할 수 있는 방식이 ε-greedy policy라는 것이다.
매우 간단한 아이디어인데,
1 - ε 의 확률로는 그냥 argmax Qπ(s, a)를 따르고,
ε의 확률로는 그냥 action a (랜덤한 action)를 따르는 것이다.
즉, 그냥 대충 확률적으로 딴 길로 샌다는 것이다.

그럼 지금까지 배운 내용을 확인해보자. (맨 아래 답이 이미 나와있는 것은 못본 걸로 하자.)
지금 까지의 예제와 비슷하게 Mars Rover의 예제를 사용한다.
그런데, a1의 경우엔 [1 0 0 0 0 0 10]의 reward를, a2의 경우엔 [0 0 0 0 0 0 5]의 reward를 갖는다.
또한, ε = 0.5이고, Trajectory = (s3, a1, 0, s2, a2, 0, s3, a1, 0, s2, a2, 0, s1, a1, 1, terminal) 이다.
이 때, First visit MC on policy Q의 값은 무엇일까?
간단하게 생각하자.
우선 a1을 취한 경우를 생각하면,
(s3, a1, 0, s2), (s1, a1, 1, terminal)의 두 가지 경우밖에 존재하지 않는다.
그리고, 𝛾=1이므로 지나온 모든 states에 final reward 1을 넣어 Q(-, a1) = [1 0 1 0 0 0 0]이 나오게 된다.
이 때 s2의 경우엔 a1의 action을 취하지 않았기 때문에 0이 들어가게 된다.
그럼 a2를 취한 경우도 생각하면,
(s2, a2, 0, s1)밖에 존재하지 않는다. (First-visit이므로 두 번 지나간건 생각하지 않는다. 사실 그거나 그거나 𝛾=1이라..)
그렇다면 위와 비슷하게, Q(-, a2) = [0 1 0 0 0 0 0]이 나오게 된다.
간단하지 않은가?

위는 ε-greedy Policy Improvement방식을 사용하면, policy는 제자리에 머무르거나 무조건 더 좋은 방향으로 갈 수 밖에 없다는 것을 증명한다.
그냥 공식으로 되어 있으니 딱히 쓸 말이 더 없을 것 같다...

여기서 GLIE (Greedy in the Limit of Infinite Exploration)에 대하여 나온다.
GLIE는 Exploration을 효율적으로 만드는 것을 목적으로 한 일종의 전략인데,
간단히 말하면 모든 (s, a)를 무한히 지나고 나면 policy를 greedy하게 만드는 것이다.
이에 대한 간단한 예로, ε의 값이 조금씩 줄어드는 ε-greedy를 생각할 수 있다.
가령, ε = 1/i로 두는 것이다.
이러면 i가 무한대로 발산하면 ε=0으로 수렴하게 되고, 결국 1-ε가 1로 수렴하게 되어 언제나 greedy한 선택을 하게 된다.
이런 방식을 바로 GLIE하다고 하는 것이다.
(좀 더 간단히 말하자면, 그냥 무한히 exploration을 지나면 greedy해지는 알고리즘을 의미한다.)

그리고 다음은 ε-greedy policy를 적용한 Monte Carlo Control 알고리즘의 의사 코드이다.
그냥 쭉쭉 읽어나가면서 이해하면 될 것 같고...
조금 신경쓸 부분만 짚어보자면,
2번째 줄. policy 를 ε-greedy(Q)로 initialize하고 있다.
6번째 줄. 위에선 First visit이라고만 적혀 있지만, Every-visit을 해도 된다.
7번째 줄. 원래 Monte Carlo면 N(s, a)가 아니라 N(s)였겠지만, On Policy Q Improvement 이므로 N(s, a)가 된다.
11번째 줄. GLIE하게 만들어 주기 위해서 ε = 1/k로 만들어준다.

이제 예제로 한번 알아보도록 하자.
언제나와 같이 Mars Rover의 예시인데,
Q(-, a1) = [1 0 1 0 0 0 0], Q(-, a2) = [0 1 0 0 0 0 0] 일때
optimal policy π(s)는 무엇이고,
k = 3, ε = 1/k 일 때 ε-greedy policy는 무엇일까?
optimal policy는 argmax Q(s, a)이므로, [a1, a2, a1, tie, tie, tie, tie] 가 된다.
참고 : state s4 이후에는 모두 Q(-, a1), Q(-, a2)의 값이 0으로 같으므로 tie가 된다.
만약 tie가 나온다면 무조건 a1을 고르거나 a2를 고르는 등의 방식도 있고 랜덤으로 하나를 고르는 방식도 있는데, 일반적으로는 랜덤으로 하나를 고르는 방식이 더 효율이 좋다.
또한, k=3, ε=1/k라면 ε-greedy policy의 경우
2/3의 확률로는 [a1, a2, a1, tie, tie, tie, tie] 를 따르고,
1/3의 확률로는 그냥 아무데나 갈 것이다.

이번에는 MC 방식이 아닌 TD 방식을 생각해보자.
어떻게 하면 model-free하게 TD방식을 만들 수 있을까?
아이디어는 또 단순하다.
TD방식과 ε-greedy 방식을 같이 사용하여 Qπ를 계산한 후에, (Policy evaluation)
π = ε-greedy (Qπ)로 두어 policy를 개선한다. (Policy Improvement)

이렇듯 TD methods에 ε-greedy policy를 적용한 것을 SARSA (states action reward states action 라는 뜻ㅎ;;)라고 한다.
간단히 SARSA가 뭔지 설명하자면 현재 state에서 action을 취한 뒤에, 다음 state에서 action을 취하고 나서 policy improvement가 이루어지는 것이다.
다르게 말하자면, 현재 (st, at) 쌍에서의 상태를 관찰한 뒤에, 다음 state st+1 에서의 action at+1을 취하고 나서,
그 뒤에 관찰한 값을 바탕으로 현재 policy π를 update 하는 것이다.
그 외의 나머지 부분은 MC 방식과 비슷하게 위의 알고리즘을 그냥 읽으면 될 것 같다.
참고로, 7번째 줄에 적혀있는 α는 learning rate이다.
이 방법의 장점으로는, 모든 episode를 다 돌지 않아도 금방금방 policy improvement를 진행할 수 있다는 것이다.
그렇기 때문에, 만약 episode 하나하나가 매우 길다면, 이 방식이 매우 효율적이게 될 것이다.
그때 그때 (s, a)쌍만 주어진다면 바로바로 policy improvement가 가능하기 때문이다.

이 부분은 조금 이론적인 부분인데,
위의 두 가지를 만족하는 α를 선택하면 SARSA는 무조건 수렴한다는 것인데,
실제 상황에서는 저런 값은 잘 선택하지 않고, 그냥 하나하나 경험적으로 집어넣어 본다고 한다.
(그러니까 그냥 이론적으로 알고만 넘어가라는 뜻 ㅎ)

Q-learning은 지금까지 배웠던 SARSA에서 아주 약간만 바꾼 방식이다.
원래 SARSA에서는 다음 state와 action 의 (st+1, at+1)의 쌍을 취해서
원래 Q(s+1, at+1)였던 것을 max Q(st+1, a')으로 바꾸어 준 것이다.
그러니까, 다음 action을 고를 때 그냥 아무거나 고르는 것이 아니라, Q의 값이 최대가 되는 action을 고른다는 얘기이다.

그리고 Q-learning에도 ε-greedy Exploration을 적용할 수 있다.
사실 SARSA랑 너무 똑같아서 딱히 할 말이 없다.
그냥 중간에 Q(st+1, at+1) 이었던 것이 max Q(st+1, a)가 된 것 뿐이다.

그리고 ε-greedy policy를 Q-learning에 적용할 때도, 위의 MC의 경우와 마찬가지로
GLIE함을 만족하여야 optimal Q*와 optimal π*를 구할 수 있다.

그런데, 원래는 unbias한 Q function을 사용하더라도, max연산을 하면 π의 예측값의 value V는 bias해질 수도 있다.
왜 그러는지는 위에 annotation으로 적혀있는 수식을 확인하면 될 것 같다.
(참고 : 1번째 줄에서 2번째줄로 넘어가는 수식에서 부등식이 생기는 이유 : 옌센 부등식 https://ko.wikipedia.org/wiki/%EC%98%8C%EC%84%BC_%EB%B6%80%EB%93%B1%EC%8B%9D)

이를 보완하기 위해서 고안된 방법이 바로 Double Learning이다.
예측치의 최댓값가 실제 값의 최댓값의 예측치로 사용되는 것을 피하기 위해서 고안되었다.
(예측치의 최댓값 <= 실제 값의 최대값의 예측치 이므로)
그래서 Q를 하나를 쓰는게 아니라 두 개 (Q1, Q2)로 나누어 사용한다.
그 중 Q1은 max action a*를 선택하는데 사용하고,
Q2는 a*의 값을 예측하는데 사용한다.
이렇게 하면, estimator가 bias해지는 것을 방지할 수 있다.

위는 Double Q-Learning의 작동 과정을 간단히 나타낸 것이다.
물론 Double Q-Learning은 Q-Learning보다 메모리 및 연산이 더 많이 필요하게 될 것이다.

하지만 특정 상황에서 Double Q-learning은 Q-learning보다 훨씬 더 빠르게 optimal한 값에 수렴할 수 있게 된다.
후반부는 강의 내에서도 교수님이 그냥 후딱후딱 넘어가는 바람에 나도 설명 후딱후딱 해버렸다.
어째 지금까지 모든 강의가 다 시간이 부족해서 후반부는 빠르게 넘어가는 느낌이다.
아무튼, 다음 CS234 5강에서 보도록 하자.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |
| 강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란? (5) | 2019.04.06 |
강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference)

- 본 포스팅은 CS234 3강의 내용을 정리합니다.

CS234 3강에선, MDP 모델 없이 Policy Evaluation하는 법에 대해 다룬다.
주로 다루는 내용은,
- Dynamic Programming
- Monte Carlo policy evaluation
- Temporal Difference(TD)
등이 있다.

저번 시간에 Dynamic Programming으로 Policy π에 대한 Evaluation에 대해 배운 바 있다.
k번째의 horizon에서 정확한 value값을 뽑아낸다고 할 때,
이 k의 값을 Value 값이 ||Vₖπ - Vₖ₋₁π|| < ε 로 수렴할 때 까지 증가시켜
infinite horizon의 value값을 찾아내는 방법이다.
이것을 그림으로 조금 더 자세히 알아보도록 하자.

위 그림은 State s에서 특정한 action들을 취하는 것을 트리형 구조로 나타낸 것이다.
State s에서 특정 Action을 취했을 때, 어떠한 state로 가게 되고
그 후에 또 Action을 취한 후 특정한 State로 가게 되고 ... 을 반복하게 된다.
Policy Evaluation에서 원하는 것은, 저 Action을 취했을 때 받는 Reward의 총 합을 얻는 것이다.
(바로 앞의 Action에서뿐만 아니라, 그 뒤에 일어날 것들을 포함한, discounted value를 의미함.)

DP 방식은 이전에 계산해 뒀던 Vₖ₋₁π의 값을 통해 Vₖπ의 값을 구한다.
이 때, DP 방식은 World의 Model인 P(s' | s, a)를 알고 있기 때문에
정확한 Vₖπ의 값을 구할 수 있다. (어떤 Action을 했을 때 어떤 reward가 들어오는지 정확히 알고 있으므로.)

즉, 여기서 알 수 있는 점은 Dynamic Programming (DP) 방식은 MDP 의 모델인 M을 필요로 한다는 것이다.
이 모델 없이는, DP는 돌아갈 수 없다.
그런데, 만약 dynamics model P 나 reward model R을 모른다면 어떻게 해야 할까?
이제부터, model없이 Policy evaluation을 하는 방법을 알아보도록 하자.

Gt와 Vπ(s)는 위의 슬라이드를 참고해서 보도록 하자.
Monte Carlo 방식은 모든 Action에 대한 Value를 평균을 내면 그 state의 value를 알 수 있다는 아이디어로 시작되었다.

만약 한 State에서 도달할 수 있는 길이 유한하다면, 그 길들을 sample을 내서 그 return의 평균을 내는 방법이다.
MDP dynamics / model이 필요하지 않다. (그냥 가능한 경우의 수를 평균낸 것이므로)
또한, DP처럼 bootstrapping (한 구간에서 계속해서 반복하는 것?) 하지 않는다.
그리고 state가 Markov하다는 가정을 하지 않는다.
결국 Monte Carlo 방식은 경험에 의존한 방법이므로, 과거에 Agent가 받았던 reward와 action등에 의해 Value가 결정되기 때문이다.
하지만, episodic MDPs (반복 가능하고 언젠간 끝나는 MDP. 예시 : 게임 Pong)의 경우에만 사용 가능하다.
여기서 episode란, 한 번의 순환을 의미한다. 가령 게임 Pong의 경우, 한번의 게임이 끝나는 것이 하나의 episode이다.

First-Visit Monte Carlo란, 처음 방문한 state의 경우에만 V를 update하는 방식이다.
N(s) (state의 방문 횟수)와 G(s)를 모든 s에 대하여 0으로 초기화해 준 다음
episode i를 위처럼 정의하고, (state s1에서 action a1을 하고 reward r1을 받고 s2로 가서 a2를 하고 r2를 받고 ... 언젠가 Terminate되고 끝)
Gi,t를 각각의 reward의 total discounted value라고 할 때,
처음 state를 방문하는 t의 경우에만 Vπ(s)를 update해준다.
가령, 내가 방문한 state가 s1, s1, s2, s2, s2, s3, s3, Terminate 순서라면,
각각 첫번째 s1,s2,s3 (1, 3, 6번째)의 경우에만 작동을 하고, 그 외의 경우에는 그냥 값을 무시하고 지나가게 된다.
(아래 예시가 나온다. 곧...)

더 자세히 들어가기 전에, Bias, Variance, MSE가 무엇인지 빠르게 알아보도록 하자.
참고로 위 용어들은 통계학 용어들이므로, 이번 포스팅에서는 그 자세한 내용은 생략하겠다.
(참고자료 - 추정량 위키백과 https://ko.wikipedia.org/wiki/%EC%B6%94%EC%A0%95%EB%9F%89)
간단하게 이야기하자면,
Bias(편향)는 예측한 값이 얼마나 한쪽으로 치우쳐져 있는가를 의미하고,
Variance(분산)는 예측한 값이 실제 측정치와 얼마나 떨어져 있는가를 의미하고,
MSE(Mean Squared Error)는 그 둘을 조합해놓은 것이다.

위 내용들을 갖고 다시 Fist-Visit Monte Carlo로 돌아오자.
Vπ의 estimator θ^은, unbiased(bias가 없는) 실제 [Gt|st = s]의 기댓값이다.
그리고 큰 수의 법칙에 의해서, N(s)가 무한대로 발산하면, 그에 따라 Vπ(s)는 실제 값에 수렴하게 된다.
(참고 : 큰 수의 법칙 https://ko.wikipedia.org/wiki/%ED%81%B0_%EC%88%98%EC%9D%98_%EB%B2%95%EC%B9%99)
하지만, 데이터 대비 비효율적이라는 단점이 존재한다.
가령, time step이 10000이 지나가도 똑같은 state만 지났었다면 그 episode에서 얻을 수 있는 정보가 1개밖에 없고
그 값으로만 Vπ를 개선하는 방식인 것이므로,
각각의 time step에 대한 데이터가 10000개가 들어와도 거기서 쓸만한 정보를 하나밖에 구해오지 못하는 것이다.

Every-Visit Monte Carlo 는 First-Visit Monte Carlo에서 약간의 변화를 준 방식이다.
이름만 봐도 알겠지만...
First-Visit Monte Carlo 방식은 State를 처음 방문했을 때에만 Vπ를 update해주었지만,
Every-Visit Monte Carlo 방식은 State를 방문할 때 마다 Vπ를 update해준다.
이 방식은 biased한 방식인데...
직관적으로 보았을 때, 한 episode에서 state 하나를 딱 한번만 뽑는다면 (First-Visit Monte Carlo의 경우엔)
G(s) = 0 + Gi,t가 되므로, 어떤 경우에서든 G(s)는 독립적인 변수가 될 것이다.
하지만, 만약 한 episode에서 state가 여러번 나온다면, (Every-Visit Monte Carlo의 경우엔)
G(s)는 다른 time t에서의 G(s)와 상관관계가 생기게 된다.
결국, Every-Visit Monte Carlo의 방법은 그 상관관계가 어느 정도 존재하는 것들을 평균을 내게 되는 것이므로,
상관관계가 높은 쪽으로 어느정도 치우쳐지게 될 것이다. (그래서 biased 해진다.)
그러나 이 Every-Visit Monte Carlo로 얻는 추정량은 일치 추정량이어서, 데이터를 많이 얻으면 얻을수록
실제 추정치에 수렴하게 된다.
그래서, 이 방식은 First-Visit Monte Carlo에 비해 훨씬 더 낮은 Variance를 갖게 된다.
그리고 경험적으로, 이렇게 나온 값이 거의 확실히 First-Visit Monte Carlo보다 MSE가 낮다. (더 좋다는 뜻이다.)


또, Incremental Monte Carlo에 대해 생각해 볼수도 있다.
Vπ(s)는 위 ppt의 방식으로 계산하여, 그 다음 ppt의 방식으로 바꿔줄 수 있다.
이 때, α가 1/N(s)라면 every visit Monte Carlo와 아예 동일한 방식이 되고, (Vπ(s) = Gi,t와 같아지므로)
α가 1/N(s)보다 크다면 오래된 data를 잊게 되는, discount factor와 약간 비슷한 느낌이 된다.

First-Visit MC 방식과 Every-Visit MC방식을 사용했을 때 V의 예측치를 찾는 문제이다.
저번 시간부터 사용해왔던 Mars rover의 예제를 다시 들고 와서
𝛾=1, R=[1,0,0,0,0,0,10]이라고 하고,
(s3, a1, 0, s2, a1, 0, s2, a1, 0, s1, a1, 1, terminal)의 방식으로 움직인다고 가정할 때,
각각의 state에서 First Visit MC의 V의 예측값은 무엇인가?
또, state s2에서 Every-Visit MC의 V의 예측값은 무엇인가?
First-Visit의 경우 각각 첫 번째 s3, s2, s1에서만 Value를 예측하고,
𝛾=1이므로 V(s1) = 1, V(s2) = 1, V(s3) = 1, 그 외 나머지 state에서는 V(s)는 0이 될 것이다.
Every-Visit의 경우도 이와 마찬가지이다.
V(s1)=1이고, s2는 두번 나오지만 V(s) = G(s) / N(s) 이므로 2/2 = 1, 즉 V(s2) = 1이 된다.

이를 아까 DP처럼 트리형 구조로 나타낸다면,
DP는 맨 위에서만 Bootstrapping을 하던 반면,
MC는 가능한 경우의 수를 샘플을 내어 평균을 내서
그 값을 reward의 예측값으로 사용하게 된다.

Monte Carlo방식의 한계점들은 다음과 같다.
- 일반적으로 variance가 높은 편이다. 이를 줄이기 위해선 많은 데이터가 필요하다.
- episodic setting이 필요하다. episode가 끝나야지만 Vπ(s)가 update되기 때문이다.

다음은 MC의 요약본이다.
위의 내용을 잘 숙지하고 넘어갈 수 있도록 하자.

다음으로 배울 내용은 TD learning이다.
이 방식은 위의 Monte-Carlo 방식과 비슷하게 Model이 필요없다.
또, DP와 같이 Bootstrap 하면서도 MC와 같이 sample을 내기도 하며,
episodic하건 infinite-horizon / non-episodic 하건 사용가능하며,
각각의 (s, a, r, s') (state, action, reward, next_state) 튜플이 지나갈 때 마다 V의 예측값을 업데이트 해 준다.
(각각의 time step마다 update한다는 뜻)

저번 시간에 잠깐 했던 벨만 방정식 (Bellman operator)을 다시 가져오자면,
Vπ(s) 는 현재 immediate reward r(s, π(s)) 와 discounted sum의 합이었다.
그리고 every-visit MC에서, Vπ(s) = Vπ(s) + α(Gi,t - Vπ(s)) 라고 정의했었다.
이 때, Gi,t를 계산하기 위해선 episode 하나를 통째로 끝날 때 까지 기다려야 했다.
그런데, 그냥 이 Gi,t를 Bellman operator로 바꾸어서, rt + 𝛾Vπ(st+1)라고 두면 어떨까?
즉, DP와 같이 다음 reward를 계산할 때, 이미 갖고 있는 데이터를 바탕으로 계산하자는 것이다.
어렵게 생각할 것 없이, 그냥 저번에 했던 DP의 방식을 조금만 차용했을 뿐이라고 생각하면 된다.
실측값인 Gi,t는 state가 Markov 하다면 Bellman Operator와 동일하게 성립하지 않겠는가?

이것을 알고리즘으로 나타내면 다음과 같다.
α값을 input으로 준 뒤에, (내가 선택하면 된다.)
모든 state에 대해 Vπ(s) = 0으로 초기화 한 뒤,
(st, at, rt, st+1) 튜플을 샘플링 하여
이 튜플을 바탕으로, 아까 제안했던 TD 공식을 사용하여
Vπ(st) = Vπ(st) + α(rt + 𝛾Vπ(st+1) - Vπ(st)) 를 그대로 반복하는 것이다.

빠른 이해를 위해, 바로 예제로 들어가보자.
아까 전과 같이 Mars rover예제로, R = [1 0 0 0 0 0 10]이라고 가정하고
s1이나 s7에 도달하면 그 뒤에 무조건 episode가 terminate 된다고 하자.
이 때, (s3, a1, 0, s2, a1, -, s2, a1, 0, s1, a1, 1, terminal) 의 튜플이 주어질 때, (ppt 오른쪽 위에 쓰여진 대로 수행된다.)
α=1에서의 TD 예측치는 무엇인가?
이를 식으로 잠시 나타내어
Vπ(st) = Vπ(st) + α(rt + 𝛾Vπ(st+1) - Vπ(st))를 위 상황에 대입하면,
α, 𝛾 모두 1이므로
Vπ(st) = Vπ(st) + rt + Vπ(st+1) - Vπ(st)
= rt + Vπ(st+1)가 된다.
모든 state s에 대해 Vπ(st) = 0으로 초기화 했으므로,
Vπ(s3) = rt + Vπ(s2)
-> Vπ(s3) = 0 + 0 = 0
Vπ(s2) = rt + Vπ(s1)
-> Vπ(s2) = 0 + 0 = 0
Vπ(s1) = rt + Vπ(terminated)
-> Vπ(s1) = 1 + 0 = 1
즉, Vπ(s1)=1, 그 외 나머지 state 에서 Vπ(s) = 0이 된다.
이것이 TD Learning과 MC의 차이점인데,
MC의 경우 Vπ(s3)를 계산할 때 모든 경로를 끝까지 계산하여, s1에 도달했을 때의 그 값 또한 Vπ(s3)의 값에 넣어두지만,
TD Learning은 그냥 s3에서 s2로 한번 간 순간 이미 Agent가 s3에 있었다는 정보를 바로 버리게 된다.
그렇기 때문에 TD learning은 추후에 s1에 도달하더라도 s3의 값에는 변화를 주지 않는다.
그리고 그렇기 때문에 TD learning은 Monte Carlo와는 다르게 episodic 하지 않아도 되는 것이다.
어차피 끝까지 가지도 않고 바로 앞에서 무슨 일이 벌어지는지만 bootstrapping하여 알아내기 때문이다.
+ 위 경우엔, α=1이었기에 아무리 반복해도 딱히 변하지를 않았지만,
α=1이 아닌 경우엔, 지속적으로 반복하면 Vπ(s2), Vπ(s3)의 값들도 조금씩 변화하며
계속 반복하게 되면 일정 값에 수렴하게 될 것이다.
가령, α=2의 경우엔,
Vπ(st) = Vπ(st) + 2 * (rt + Vπ(st+1) - Vπ(st))
= 2 * (rt + Vπ(st+1)) - Vπ(st) 가 된다.
이 때는 Vπ(st)의 값들이 어떻게 바뀌는지는, 직접 해보며 익히길 바란다.
++ 참고로, α=1인 경우의 TD update Vπ(st) = rt + Vπ(st+1)는 TD(0)이라고도 한다!

이를 트리형 구조로 나타내면 다음과 나타낼 수 있다.
TD는 value를 예측하기 위해 st+1을 샘플링 하여 기댓값의 근사값을 찾아내고,
V(st+1)의 예측치를 활용하여 DP와 비슷하게 bootstrapping하여 value를 update한다.
일종의 MC와 DP의 짬뽕 느낌이 확 들지 않는가?

그럼, 이제부터 DP, MC, TD의 속성들을 비교해보자.
- model 없이 사용 가능한가?
우선, DP는 무조건 MDP가 필요한 방법이므로 X
MC, TD는 경우의 수를 샘플링 하는 방식으로 진행되므로, model-free하다. O
- non-episodic한 경우 사용 가능한가?
MC의 경우 episode 한번이 끝날때 마다 update하는 방식이므로, 무조건 episodic한 경우여야 한다. X
DP, TD의 경우 bootstrapping하여 Vπ(s)를 얻어내는 방식이므로, non-episodic / infinite episodic의 경우도 가능하다. O
- Non-Markovian할 때 사용 가능한가?
MC의 경우 그저 가능한 경우의 수를 나열하는 것이므로, Markovian하건 안하건 그냥 평균만 내면 되는 방식이다. O
DP, TD의 경우 state가 Markov하다는 전제 하에 bootstrapping을 하는 것이므로, state는 Markovian 해야 한다. X
- 극한값에서 실제 값에 수렴하는가?
DP, TD는 bootstrapping을 하면 할수록 수렴하고, MC의 경우도 episode를 무수히 반복하다 보면 큰 수의 법칙에 의해 수렴한다. O
- unbiased한가?
MC의 경우, First-Visit MC는 unbiased 하지만, Every-Visit MC는 biased하다. O
TD의 경우, bias가 있다고 할 수 있다.
가령 아까 위의 Check your understanding에서, α=2의 경우에 첫 번째 반복에선 Vπ(s1)만 reward가 1이라고 되는 편향이 생긴다.
(다르게 이야기하자면, s3, s2일 경우에 reward가 0이라는 편향값이 생긴다고 보면 될 것 같다. 즉, 정확하지 못하다는 것이다.)
DP의 경우가 제일 특이한데, Vπ(s+1)의 값은 Model을 통해 얻는 정확한 값이므로 Bias가 있다고 하기엔 애매한 감이 있다. NA

그리고, MC, TD 등의 알고리즘을 선택할 때 Bias/variance, Data efficiency, Computational efficiency와 같은 점들을 고려해야 한다.
(이 근방 부분은 나중에 더 자세히 다루겠다고 하신다.)

이번에 생각할 내용은 Batch (Offline이라고도 한다?) solution에 대한 내용이다.
K개의 finite한 episode가 있을 때, K에서 반복적으로 샘플링을 해서 MC 또는 TD(0)의 방식을 적용할 때,
MC와 TD(0)은 어떻게 수렴할까?
* TD(0)은 α=1일 때의 TD를 의미함.

다음 예시를 보도록 하자.
𝛾=1이라고 가정하자.
오른쪽 위의 노드 그림과 같은 State가 있다.
다음과 같은 8개의 에피소드가 존재한다;
- A, 0, B, 0
- B, 1 (6번 반복)
- B, 0
(이 때, A,B는 state, 0,1은 reward를 의미한다.)
이 때, MC와 TD(0)방식의 V(A), V(B)는 어떻게 수렴할까?
우선 V(B)부터 보도록 하자.
MC를 사용하면, 결국 B는 8번의 episode가 존재하고 그중 6개의 episode에서 1의 reward를 받았으므로,
V(B) = 6/8 = 3/4가 될 것이다. (무한히 많이 반복하면 이렇게 수렴하게 된다는 뜻이다!)
TD(0)를 사용하더라도 결국 sampling 후 무한정 bootstrapping하다 보면, 6/8 = 3/4로 수렴하게 될 것이다.
하지만, V(A)의 경우는 조금 다르다.
MC를 사용하게 되면, A는 언제나 A, 0, B, 0으로 갔으므로, V(A) = 0이라고 생각할 것이다.
(이 episode 들 중 A에서 출발하는 경로는 단 하나이고, 언제나 0의 reward를 뽑아냈기 때문이다.)
하지만 TD(0)를 사용하게 되면, 이야기가 조금 달라지게 된다.
TD(0)에서 사용했던 공식을 다시 한번 가져오자면,
Vπ(st) = rt + 𝛾Vπ(st+1) 였고,
𝛾=1이라고 했으므로 Vπ(st) = rt + Vπ(st+1)이 된다.
즉 Vπ(A) = rt + Vπ(st+1)
= 0 + Vπ(B)
= 0 + 3/4
= 3/4
그러므로 MC를 사용했을 때의 V(A) = 0, TD(0)을 사용했을 때의 V(A) = 3/4라는, 다른 값이 나오게 된다.

이것을 통해 MC와 TD가 Batch setting에서 수렴하는 방식의 차이를 알 수 있다.
MC의 경우는 MSE (Mean Squared Error)를 최소화하는 방식으로 수렴하게 되어,
이미 관찰된 return에 대한 오차를 최소화하는 방식이다.
TD(0)같은 경우, MDP에 최대한 가깝게 수렴하는데,
가령 P(B|A) = 1이고, r(B) = 3/4, r(A) = 0이므로 V(A) = 3/4라고 예측하는 것이다.
(이는 TD가 Markov structure을 사용하기 때문이다. MC는 Markov structure가 아니기에, MSE만을 최소화한다.)
여기까지 CS234 3강의 내용이었다.
쓰다보니 엄청나게 길게 쓴 것 같다.
여기까지 읽는 사람은 없을 것 같아서 쓰는 말이지만,
통계학 공부를 조금 더 하고 나서 인공지능을 다시 배워야될 것 같은 걱정이 들기 시작한다.
게다가 죄다 영어로 써져 있어서 직역해야 하는건지 수학 용어인지도 모르는 것들이 쑥쑥 나와서
다른 강의보다 더 쓰기 힘들었던 것 같다.
아무튼 다음 CS234 4강에서 보도록 하자.
수고링 ㅎ
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |
| 강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란? (5) | 2019.04.06 |