인공지능
-
CS234 Assignments 1-1 Solution 및 풀이2019.04.25
-
CS234 Assignment 1 해석2019.04.19
-
강화 학습 개념 정리노트 - CS234 1강 (강화 학습의 개념, MDP)2019.04.09
강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning

- 본 포스팅은 CS234 4강의 내용을 정리합니다.

이번 강의에선,
- Generalized Policy Iteration
- Importance of Exploration
- Monte Carlo Control
- Temporal Difference (TD) Methods for Control
- Maximization Bias
등에 대해 배운다.

On-policy learning이란 직접 경험한 내용을 바탕으로 policy를 예측하고, 개선해 나가는 과정이다.
즉, Agent가 직접 행한 내용에 대해서만 학습을 하는 것이다.
Off-policy learning은 그와 달리 이미 알고 있는 내용들을 바탕으로 아직 실행하지 않은 내용까지 예측해서 policy를 개선해 나가는 것이다.
가령, 다음과 같은 state와 action에 대한 policy를 생각해보자:
s1, a1, s1, a1
s1, a2, s1, a2
off-policy learning의 경우엔 위의 두 가지 policy를 조합하여
s1, a1, s1, a2
의 policy도 수행할 수 있게 된다.

이제 Policy Iteration이 뭔지 다시 한번 불러와 보자.
Policy Iteration이 뭐였느냐 한다면...
우선 Vπ를 계산해 준 다음,
그 값과 Reward model R, dynamics P를 바탕으로 policy를 개선해 나가는 과정이었다.
(자세한 내용은 2강에서 확인하도록 하자.)
그런데, Policy Iteration의 경우엔, 정확한 Reward model과 dynamics(~~가 일어날 확률)가 필요했다.
그래서 저번 강의에서는 model-free policy evaluation에 대해 설명했었는데,
이걸 한번 Policy Iteration에 써먹어 보도록 하자.

그래서 나온 것이 Model Free Policy Iteration이다.
아이디어는 그냥 Reward model과 dynamics를 Q function으로 합쳐버려서
Qπ를 계산하고 이 π를 개선해 나가면 되지 않을까? 하는 생각인 것이다.

이번엔 Monte Carlo for On Policy Q Evaluation에 대해 알아보자.
이는 저번에 배웠던 Monte Carlo for on policy value evaluation과 매우 유사한데,
원래 value evaluation에서는 N(s), G(s)를 썼지만,
Q Evaluation에서는 N(s, a) 와 G(s, a)를 사용한다.
(사실 어느 정도 당연한 이야기인데... Q는 state뿐만 아니라 action 또한 사용하는 function이기 때문이다.)
즉, 원래는 State만을 사용하던 것에서 벗어나서, State, action 쌍을 사용하는 것이다.

이 방식으로, Policy Improvement를 더욱 간단히 만들 수 있다.
그냥 Qπ(s, a)의 argmax를 취하면 그게 다음 policy가 되는 것이다.

그리고 이 방식을 사용하면 Policy Iteration을 매우 간단하게, 그리고 Model-free하게 만들 수 있다.
하지만, 아직 신경써야 할 부분이 있다. 바로 Qπ를 compute하는 부분이다.
만약 policy가 Deterministic 할 때는 policy 안에 특정 action이 존재하지 않는다면, 그 action에 대한 Q function은 절대로 계산하지 못한다.
(결국엔 Deterministic 하다면 policy에 있는 action만 따라가니깐..)

이를 해결하고 model-free한 Qπ를 계산하기 위하여, Exploration을 해야 한다!

이 때 사용할 수 있는 방식이 ε-greedy policy라는 것이다.
매우 간단한 아이디어인데,
1 - ε 의 확률로는 그냥 argmax Qπ(s, a)를 따르고,
ε의 확률로는 그냥 action a (랜덤한 action)를 따르는 것이다.
즉, 그냥 대충 확률적으로 딴 길로 샌다는 것이다.

그럼 지금까지 배운 내용을 확인해보자. (맨 아래 답이 이미 나와있는 것은 못본 걸로 하자.)
지금 까지의 예제와 비슷하게 Mars Rover의 예제를 사용한다.
그런데, a1의 경우엔 [1 0 0 0 0 0 10]의 reward를, a2의 경우엔 [0 0 0 0 0 0 5]의 reward를 갖는다.
또한, ε = 0.5이고, Trajectory = (s3, a1, 0, s2, a2, 0, s3, a1, 0, s2, a2, 0, s1, a1, 1, terminal) 이다.
이 때, First visit MC on policy Q의 값은 무엇일까?
간단하게 생각하자.
우선 a1을 취한 경우를 생각하면,
(s3, a1, 0, s2), (s1, a1, 1, terminal)의 두 가지 경우밖에 존재하지 않는다.
그리고, 𝛾=1이므로 지나온 모든 states에 final reward 1을 넣어 Q(-, a1) = [1 0 1 0 0 0 0]이 나오게 된다.
이 때 s2의 경우엔 a1의 action을 취하지 않았기 때문에 0이 들어가게 된다.
그럼 a2를 취한 경우도 생각하면,
(s2, a2, 0, s1)밖에 존재하지 않는다. (First-visit이므로 두 번 지나간건 생각하지 않는다. 사실 그거나 그거나 𝛾=1이라..)
그렇다면 위와 비슷하게, Q(-, a2) = [0 1 0 0 0 0 0]이 나오게 된다.
간단하지 않은가?

위는 ε-greedy Policy Improvement방식을 사용하면, policy는 제자리에 머무르거나 무조건 더 좋은 방향으로 갈 수 밖에 없다는 것을 증명한다.
그냥 공식으로 되어 있으니 딱히 쓸 말이 더 없을 것 같다...

여기서 GLIE (Greedy in the Limit of Infinite Exploration)에 대하여 나온다.
GLIE는 Exploration을 효율적으로 만드는 것을 목적으로 한 일종의 전략인데,
간단히 말하면 모든 (s, a)를 무한히 지나고 나면 policy를 greedy하게 만드는 것이다.
이에 대한 간단한 예로, ε의 값이 조금씩 줄어드는 ε-greedy를 생각할 수 있다.
가령, ε = 1/i로 두는 것이다.
이러면 i가 무한대로 발산하면 ε=0으로 수렴하게 되고, 결국 1-ε가 1로 수렴하게 되어 언제나 greedy한 선택을 하게 된다.
이런 방식을 바로 GLIE하다고 하는 것이다.
(좀 더 간단히 말하자면, 그냥 무한히 exploration을 지나면 greedy해지는 알고리즘을 의미한다.)

그리고 다음은 ε-greedy policy를 적용한 Monte Carlo Control 알고리즘의 의사 코드이다.
그냥 쭉쭉 읽어나가면서 이해하면 될 것 같고...
조금 신경쓸 부분만 짚어보자면,
2번째 줄. policy 를 ε-greedy(Q)로 initialize하고 있다.
6번째 줄. 위에선 First visit이라고만 적혀 있지만, Every-visit을 해도 된다.
7번째 줄. 원래 Monte Carlo면 N(s, a)가 아니라 N(s)였겠지만, On Policy Q Improvement 이므로 N(s, a)가 된다.
11번째 줄. GLIE하게 만들어 주기 위해서 ε = 1/k로 만들어준다.

이제 예제로 한번 알아보도록 하자.
언제나와 같이 Mars Rover의 예시인데,
Q(-, a1) = [1 0 1 0 0 0 0], Q(-, a2) = [0 1 0 0 0 0 0] 일때
optimal policy π(s)는 무엇이고,
k = 3, ε = 1/k 일 때 ε-greedy policy는 무엇일까?
optimal policy는 argmax Q(s, a)이므로, [a1, a2, a1, tie, tie, tie, tie] 가 된다.
참고 : state s4 이후에는 모두 Q(-, a1), Q(-, a2)의 값이 0으로 같으므로 tie가 된다.
만약 tie가 나온다면 무조건 a1을 고르거나 a2를 고르는 등의 방식도 있고 랜덤으로 하나를 고르는 방식도 있는데, 일반적으로는 랜덤으로 하나를 고르는 방식이 더 효율이 좋다.
또한, k=3, ε=1/k라면 ε-greedy policy의 경우
2/3의 확률로는 [a1, a2, a1, tie, tie, tie, tie] 를 따르고,
1/3의 확률로는 그냥 아무데나 갈 것이다.

이번에는 MC 방식이 아닌 TD 방식을 생각해보자.
어떻게 하면 model-free하게 TD방식을 만들 수 있을까?
아이디어는 또 단순하다.
TD방식과 ε-greedy 방식을 같이 사용하여 Qπ를 계산한 후에, (Policy evaluation)
π = ε-greedy (Qπ)로 두어 policy를 개선한다. (Policy Improvement)

이렇듯 TD methods에 ε-greedy policy를 적용한 것을 SARSA (states action reward states action 라는 뜻ㅎ;;)라고 한다.
간단히 SARSA가 뭔지 설명하자면 현재 state에서 action을 취한 뒤에, 다음 state에서 action을 취하고 나서 policy improvement가 이루어지는 것이다.
다르게 말하자면, 현재 (st, at) 쌍에서의 상태를 관찰한 뒤에, 다음 state st+1 에서의 action at+1을 취하고 나서,
그 뒤에 관찰한 값을 바탕으로 현재 policy π를 update 하는 것이다.
그 외의 나머지 부분은 MC 방식과 비슷하게 위의 알고리즘을 그냥 읽으면 될 것 같다.
참고로, 7번째 줄에 적혀있는 α는 learning rate이다.
이 방법의 장점으로는, 모든 episode를 다 돌지 않아도 금방금방 policy improvement를 진행할 수 있다는 것이다.
그렇기 때문에, 만약 episode 하나하나가 매우 길다면, 이 방식이 매우 효율적이게 될 것이다.
그때 그때 (s, a)쌍만 주어진다면 바로바로 policy improvement가 가능하기 때문이다.

이 부분은 조금 이론적인 부분인데,
위의 두 가지를 만족하는 α를 선택하면 SARSA는 무조건 수렴한다는 것인데,
실제 상황에서는 저런 값은 잘 선택하지 않고, 그냥 하나하나 경험적으로 집어넣어 본다고 한다.
(그러니까 그냥 이론적으로 알고만 넘어가라는 뜻 ㅎ)

Q-learning은 지금까지 배웠던 SARSA에서 아주 약간만 바꾼 방식이다.
원래 SARSA에서는 다음 state와 action 의 (st+1, at+1)의 쌍을 취해서
원래 Q(s+1, at+1)였던 것을 max Q(st+1, a')으로 바꾸어 준 것이다.
그러니까, 다음 action을 고를 때 그냥 아무거나 고르는 것이 아니라, Q의 값이 최대가 되는 action을 고른다는 얘기이다.

그리고 Q-learning에도 ε-greedy Exploration을 적용할 수 있다.
사실 SARSA랑 너무 똑같아서 딱히 할 말이 없다.
그냥 중간에 Q(st+1, at+1) 이었던 것이 max Q(st+1, a)가 된 것 뿐이다.

그리고 ε-greedy policy를 Q-learning에 적용할 때도, 위의 MC의 경우와 마찬가지로
GLIE함을 만족하여야 optimal Q*와 optimal π*를 구할 수 있다.

그런데, 원래는 unbias한 Q function을 사용하더라도, max연산을 하면 π의 예측값의 value V는 bias해질 수도 있다.
왜 그러는지는 위에 annotation으로 적혀있는 수식을 확인하면 될 것 같다.
(참고 : 1번째 줄에서 2번째줄로 넘어가는 수식에서 부등식이 생기는 이유 : 옌센 부등식 https://ko.wikipedia.org/wiki/%EC%98%8C%EC%84%BC_%EB%B6%80%EB%93%B1%EC%8B%9D)

이를 보완하기 위해서 고안된 방법이 바로 Double Learning이다.
예측치의 최댓값가 실제 값의 최댓값의 예측치로 사용되는 것을 피하기 위해서 고안되었다.
(예측치의 최댓값 <= 실제 값의 최대값의 예측치 이므로)
그래서 Q를 하나를 쓰는게 아니라 두 개 (Q1, Q2)로 나누어 사용한다.
그 중 Q1은 max action a*를 선택하는데 사용하고,
Q2는 a*의 값을 예측하는데 사용한다.
이렇게 하면, estimator가 bias해지는 것을 방지할 수 있다.

위는 Double Q-Learning의 작동 과정을 간단히 나타낸 것이다.
물론 Double Q-Learning은 Q-Learning보다 메모리 및 연산이 더 많이 필요하게 될 것이다.

하지만 특정 상황에서 Double Q-learning은 Q-learning보다 훨씬 더 빠르게 optimal한 값에 수렴할 수 있게 된다.
후반부는 강의 내에서도 교수님이 그냥 후딱후딱 넘어가는 바람에 나도 설명 후딱후딱 해버렸다.
어째 지금까지 모든 강의가 다 시간이 부족해서 후반부는 빠르게 넘어가는 느낌이다.
아무튼, 다음 CS234 5강에서 보도록 하자.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |
| 강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란? (5) | 2019.04.06 |
강화 학습 개념 정리노트 - CS234 2강 (MDP / MRP / Policy Iteration / Value Iteration)

본 포스팅은 강화 학습 강의인 CS234 2강의 내용을 정리합니다.
매우 간단하게 용어 정리 및 공식만 적으므로, 자세한 내용은 강의 정리 포스팅을 보시기 바랍니다.

Markov Process : Markov한 상태를 띄는 Action / Control이 없는 random한 state들의 집합.
이를 행렬으로 나타낸 것을 Markov Chain 이라고 부른다.

Markov Reward Process (MRP) : Markov Process + Reward.
Markov Process에다가 Reward를 추가함.

Horizon : 각각의 에피소드에 대한 time step의 개수.
Return function (Gₜ) - time step t부터 horizon까지의 reward의 discounted sum.
State Value Function (V(s)) - state s에서 얻을 수 있는 reward의 기댓값.
Discount Factor (𝛾) - immediate reward (즉각적 보상)과 future reward (미래에 얻을 보상)과의 연관관계.
0이면 연관 없음, 1이면 immediate = future

일반적으로 MRP value를 계산하는데 Dynamic Programming 방식이 사용됨. (Iterative Algorithm이라고도 함.)
Vₖ(s) = R(s) + ∑s'∈S 𝛾P(s'|s) Vₖ₋₁(s')
(위 ppt에 더 정확하게 나와있음.)

Markov Decision Process (MDP) - MRP + Action.
이젠 Action까지 포함되어 있음.
(S, A, P, R, 𝛾)의 튜플로 표현함.
지금까지의 기호들을 설명하자면,
S는 Markov State s의 집합.
A는 actions 의 집합.
P는 각 action에 따른 dymanics/transition model. (위의 MRP / MP와 다르게 action이 포함되어 있음!)
R은 Reward function으로, 각 state와 action에 따른 reward의 기댓값.
𝛾는 Discount Factor.

Policy : 각각의 state에서 어떤 action을 취할지를 선택하는 것. (그냥 말 그대로 정책이다.)
Deterministic : 결정론적임. 취하고자 하는 행동은 무조건 일어남.
Stochastic : 무작위적임. 취하고자 하는 행동이 확률적으로 일어나거나 일어나지 않을 수도 있음.

MDP + Policy = MRP이다.
이를 활용하여, MDP의 Policy Evaluation에서도 MRP와 비슷한 공식을 응용할 수 있다.

MDP Control : optimal policy를 계산함.
이때 optimal policy는 π*(s)로 표현함.
optimal policy는 유니크한 optimal value function을 가짐.

Policy Iteration : optimal policy를 구하기 위한 Iterative Algorithm.
현재 policy가 특정 값에 수렴할 때까지 지속적으로 policy를 바꿔준다.

State-Action Value Qπ(s, a)
Qπ(s, a) = R(s, a) + 𝛾∑s'∈S P(s'|s, a)Vπ(s')
로 정의되는 함수.

Policy Improvement : Policy를 강화함.
모든 state와 action 중에서 Qπ(s,a) 값이 가장 큰 state s,action a를 구해서 그 값들을 policy로 적용시킴.

즉, Policy Iteration (PI) 는 다음과 같은 행동을 반복한다.
πᵢ의 값 V을 구한다.
그 값을 사용하여 Q(s,a)도 구한 뒤,
Policy Improvement를 사용하여 πᵢ₊₁을 구함.
이를 ||πᵢ - πᵢ₋₁||₁ > 0 일 때까지 (즉, 새로운 policy와 저번 policy의 차이가 없을 때까지) 반복함.
이러면 optimal policy를 찾아낼 수 있다!



(위 세 슬라이드는 수학적 내용임으로 설명하진 않으나, ppt를 보면 이해가 갈 것임.)

Value Iteration (VI) : Value를 활용하여 optimal policy를 구하는 방법.
V의 값이 수렴할 때 까지,
최대의 Reward가 나오는 R(s, a)와 𝛾∑s'∈S P(s'|s,a)Vπ(s') 를 더한 값을 V에 집어넣어줌.
PI와는 다르게 Policy Improvement 과정 없이 진행됨.
'인공지능 > 강화 학습 개념 정리노트 (CS234)' 카테고리의 다른 글
| 강화 학습 개념 정리노트 - CS234 1강 (강화 학습의 개념, MDP) (0) | 2019.04.09 |
|---|
CS234 Assignments 1-1 Solution 및 풀이
해석본은 아래 글에 있습니다. 여기서는 풀이만 하도록 하겠습니다.

(a) optimal action은 (최적의 action은) 어떤 state si에서든 G에 도달할 때 까지 오른쪽으로 가는 것이다 (action a0을 취하는 것이다). 이 때, 모든 state si와 goal state G에서의 optimal value function을 구하여라. [5점]
optimal value function V(s) = R(s) + 𝛾Σ s'∈S P(s'|s)V(s') 이다.
이 때, action은 무조건 오른쪽으로 가는 것이고, deterministic한 상황이기 때문에 P(s'|s) = 1이 된다. (s'의 경우의 수는 1개이다.)
이를 정리하면,
V(s) = R(s) + 𝛾Σ s'∈S V(s')
이 때, s'은 s의 바로 오른쪽 (s=G일 때는 G)가 될 것이다.
이를 사용해 goal state G에서의 optimal value function을 구해 보면,
V(G) = R(G) + 𝛾Σ s'∈S V(G)
V(G) = 1 + 𝛾 + 𝛾^2 + 𝛾^3 + ....
= 1/(1-𝛾) (등비급수)
V(sₙ₋₁) = R(G) + 𝛾Σ s'∈S V(s')
= 0 + 𝛾 + 𝛾^2 + 𝛾^3 + ....
= 𝛾/(1-𝛾)
......
V(s₁) = 0 + 0 + 0 + ... + 𝛾ⁿ + 𝛾ⁿ⁺¹ + ....
= 𝛾ⁿ / 1-𝛾
(b) optimal policy가 discount factor 𝛾의 영향을 받는지에 대해 서술하시오. [5점]
optimal policy의 경우, 0<𝛾인 모든 상황에서는 위의 '무조건 오른쪽으로 가는' action을 취할 것이다.
하지만 𝛾=0인 경우엔 0<𝛾인 경우와 비슷하게 무조건 오른쪽으로 가는 action만을 취하겠지만, 그 policy 말고 다른 policy 또한 optimal policy가 될 수 있다.
(오른쪽 왼쪽 오른쪽 오른쪽 오른쪽 .... 도 optimal policy라 할 수 있다.)
(c) 모든 reward 에 상수 c를 더한다고 생각해보자. (즉, G에서는 reward 1+c를, 나머지 state에서는 reward c를 받는다.)
이 때, 모든 si와 G에 대한 새로운 optimal value function을 구하시오. 상수 c를 더한 것이 optimal policy를 바꾸는가? 답을 설명하시오. [5점]
영향을 끼치지 않는다.
직관적으로 보자면, 어떤 상수 c를 더한다고 해도 결국 reward가 가장 큰 것을 G일 것이므로,
optimal policy는 언제나 오른쪽으로 가는 action을 취하는 policy이라는 점은 변하지 않는다.
optimal value function을 구하면,
c를 더한 V(s)를 new_V(s), 원래 V(s)를 old_V(s)라 할때,
new_V(s) = old_V(s) + c + 𝛾c + 𝛾^2c + ....
= old_V(s) + c/(1-𝛾)
(d) 모든 reward에 상수 c를 더하고 상수 a를 곱한다고 해보자. (new_r = a * (c + old_r)) 이 때 모든 si와 G에 대한 새로운 optimal value function을 구하여라. 이것이 optimal policy에 변화를 주었는가? 답을 설명하고, 만약 '그렇다'고 답했다면 optimal policy를 바꾸는 a와 c의 예시를 드시오. [5점]
우선 위의 방식으로 optimal value function을 구하면,
new_V(s) = a * (old_V(s) + c + 𝛾c + 𝛾^2c + .... )
= a * old_V(s) + ac/(1-𝛾)
가 된다.
이 때 a>0이라면 optimal policy는 원래와 같이 goal state G로 곧장 가는, 무조건 오른쪽으로만 가는 policy가 될 것이다.
a=0이라면, 모든 reward가 0이 되므로 모든 value function과 policy가 optimal 해 진다. (바람직하진 못하겠지만)
a<0이라면, goal state G가 가장 낮은 reward를 갖게 되므로, goal state G를 거치지 않는 모든 policy는 모두 optimal policy가 될 것이다. (즉, G를 지나는 policy는 optimal 하지 못하다.)
또한, c의 값은 어떻게 변해도 아무런 영향을 끼치지 않는다.
Assignment 1 중에서 가장 쉬운 난이도 문제였습니다.
Value function의 공식을 알고 있는지,
Optimal policy와 Optimal value function의 개념을 알고 있는지,
그리고 value function의 공식을 응용할 수 있는지에 대해 묻는 문제들이었습니다.
사실상 공식에 대입하는 문제였네요 ㅎㅎ
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
| CS234 Assignment 1 해석 (0) | 2019.04.19 |
강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference)

- 본 포스팅은 CS234 3강의 내용을 정리합니다.

CS234 3강에선, MDP 모델 없이 Policy Evaluation하는 법에 대해 다룬다.
주로 다루는 내용은,
- Dynamic Programming
- Monte Carlo policy evaluation
- Temporal Difference(TD)
등이 있다.

저번 시간에 Dynamic Programming으로 Policy π에 대한 Evaluation에 대해 배운 바 있다.
k번째의 horizon에서 정확한 value값을 뽑아낸다고 할 때,
이 k의 값을 Value 값이 ||Vₖπ - Vₖ₋₁π|| < ε 로 수렴할 때 까지 증가시켜
infinite horizon의 value값을 찾아내는 방법이다.
이것을 그림으로 조금 더 자세히 알아보도록 하자.

위 그림은 State s에서 특정한 action들을 취하는 것을 트리형 구조로 나타낸 것이다.
State s에서 특정 Action을 취했을 때, 어떠한 state로 가게 되고
그 후에 또 Action을 취한 후 특정한 State로 가게 되고 ... 을 반복하게 된다.
Policy Evaluation에서 원하는 것은, 저 Action을 취했을 때 받는 Reward의 총 합을 얻는 것이다.
(바로 앞의 Action에서뿐만 아니라, 그 뒤에 일어날 것들을 포함한, discounted value를 의미함.)

DP 방식은 이전에 계산해 뒀던 Vₖ₋₁π의 값을 통해 Vₖπ의 값을 구한다.
이 때, DP 방식은 World의 Model인 P(s' | s, a)를 알고 있기 때문에
정확한 Vₖπ의 값을 구할 수 있다. (어떤 Action을 했을 때 어떤 reward가 들어오는지 정확히 알고 있으므로.)

즉, 여기서 알 수 있는 점은 Dynamic Programming (DP) 방식은 MDP 의 모델인 M을 필요로 한다는 것이다.
이 모델 없이는, DP는 돌아갈 수 없다.
그런데, 만약 dynamics model P 나 reward model R을 모른다면 어떻게 해야 할까?
이제부터, model없이 Policy evaluation을 하는 방법을 알아보도록 하자.

Gt와 Vπ(s)는 위의 슬라이드를 참고해서 보도록 하자.
Monte Carlo 방식은 모든 Action에 대한 Value를 평균을 내면 그 state의 value를 알 수 있다는 아이디어로 시작되었다.

만약 한 State에서 도달할 수 있는 길이 유한하다면, 그 길들을 sample을 내서 그 return의 평균을 내는 방법이다.
MDP dynamics / model이 필요하지 않다. (그냥 가능한 경우의 수를 평균낸 것이므로)
또한, DP처럼 bootstrapping (한 구간에서 계속해서 반복하는 것?) 하지 않는다.
그리고 state가 Markov하다는 가정을 하지 않는다.
결국 Monte Carlo 방식은 경험에 의존한 방법이므로, 과거에 Agent가 받았던 reward와 action등에 의해 Value가 결정되기 때문이다.
하지만, episodic MDPs (반복 가능하고 언젠간 끝나는 MDP. 예시 : 게임 Pong)의 경우에만 사용 가능하다.
여기서 episode란, 한 번의 순환을 의미한다. 가령 게임 Pong의 경우, 한번의 게임이 끝나는 것이 하나의 episode이다.

First-Visit Monte Carlo란, 처음 방문한 state의 경우에만 V를 update하는 방식이다.
N(s) (state의 방문 횟수)와 G(s)를 모든 s에 대하여 0으로 초기화해 준 다음
episode i를 위처럼 정의하고, (state s1에서 action a1을 하고 reward r1을 받고 s2로 가서 a2를 하고 r2를 받고 ... 언젠가 Terminate되고 끝)
Gi,t를 각각의 reward의 total discounted value라고 할 때,
처음 state를 방문하는 t의 경우에만 Vπ(s)를 update해준다.
가령, 내가 방문한 state가 s1, s1, s2, s2, s2, s3, s3, Terminate 순서라면,
각각 첫번째 s1,s2,s3 (1, 3, 6번째)의 경우에만 작동을 하고, 그 외의 경우에는 그냥 값을 무시하고 지나가게 된다.
(아래 예시가 나온다. 곧...)

더 자세히 들어가기 전에, Bias, Variance, MSE가 무엇인지 빠르게 알아보도록 하자.
참고로 위 용어들은 통계학 용어들이므로, 이번 포스팅에서는 그 자세한 내용은 생략하겠다.
(참고자료 - 추정량 위키백과 https://ko.wikipedia.org/wiki/%EC%B6%94%EC%A0%95%EB%9F%89)
간단하게 이야기하자면,
Bias(편향)는 예측한 값이 얼마나 한쪽으로 치우쳐져 있는가를 의미하고,
Variance(분산)는 예측한 값이 실제 측정치와 얼마나 떨어져 있는가를 의미하고,
MSE(Mean Squared Error)는 그 둘을 조합해놓은 것이다.

위 내용들을 갖고 다시 Fist-Visit Monte Carlo로 돌아오자.
Vπ의 estimator θ^은, unbiased(bias가 없는) 실제 [Gt|st = s]의 기댓값이다.
그리고 큰 수의 법칙에 의해서, N(s)가 무한대로 발산하면, 그에 따라 Vπ(s)는 실제 값에 수렴하게 된다.
(참고 : 큰 수의 법칙 https://ko.wikipedia.org/wiki/%ED%81%B0_%EC%88%98%EC%9D%98_%EB%B2%95%EC%B9%99)
하지만, 데이터 대비 비효율적이라는 단점이 존재한다.
가령, time step이 10000이 지나가도 똑같은 state만 지났었다면 그 episode에서 얻을 수 있는 정보가 1개밖에 없고
그 값으로만 Vπ를 개선하는 방식인 것이므로,
각각의 time step에 대한 데이터가 10000개가 들어와도 거기서 쓸만한 정보를 하나밖에 구해오지 못하는 것이다.

Every-Visit Monte Carlo 는 First-Visit Monte Carlo에서 약간의 변화를 준 방식이다.
이름만 봐도 알겠지만...
First-Visit Monte Carlo 방식은 State를 처음 방문했을 때에만 Vπ를 update해주었지만,
Every-Visit Monte Carlo 방식은 State를 방문할 때 마다 Vπ를 update해준다.
이 방식은 biased한 방식인데...
직관적으로 보았을 때, 한 episode에서 state 하나를 딱 한번만 뽑는다면 (First-Visit Monte Carlo의 경우엔)
G(s) = 0 + Gi,t가 되므로, 어떤 경우에서든 G(s)는 독립적인 변수가 될 것이다.
하지만, 만약 한 episode에서 state가 여러번 나온다면, (Every-Visit Monte Carlo의 경우엔)
G(s)는 다른 time t에서의 G(s)와 상관관계가 생기게 된다.
결국, Every-Visit Monte Carlo의 방법은 그 상관관계가 어느 정도 존재하는 것들을 평균을 내게 되는 것이므로,
상관관계가 높은 쪽으로 어느정도 치우쳐지게 될 것이다. (그래서 biased 해진다.)
그러나 이 Every-Visit Monte Carlo로 얻는 추정량은 일치 추정량이어서, 데이터를 많이 얻으면 얻을수록
실제 추정치에 수렴하게 된다.
그래서, 이 방식은 First-Visit Monte Carlo에 비해 훨씬 더 낮은 Variance를 갖게 된다.
그리고 경험적으로, 이렇게 나온 값이 거의 확실히 First-Visit Monte Carlo보다 MSE가 낮다. (더 좋다는 뜻이다.)


또, Incremental Monte Carlo에 대해 생각해 볼수도 있다.
Vπ(s)는 위 ppt의 방식으로 계산하여, 그 다음 ppt의 방식으로 바꿔줄 수 있다.
이 때, α가 1/N(s)라면 every visit Monte Carlo와 아예 동일한 방식이 되고, (Vπ(s) = Gi,t와 같아지므로)
α가 1/N(s)보다 크다면 오래된 data를 잊게 되는, discount factor와 약간 비슷한 느낌이 된다.

First-Visit MC 방식과 Every-Visit MC방식을 사용했을 때 V의 예측치를 찾는 문제이다.
저번 시간부터 사용해왔던 Mars rover의 예제를 다시 들고 와서
𝛾=1, R=[1,0,0,0,0,0,10]이라고 하고,
(s3, a1, 0, s2, a1, 0, s2, a1, 0, s1, a1, 1, terminal)의 방식으로 움직인다고 가정할 때,
각각의 state에서 First Visit MC의 V의 예측값은 무엇인가?
또, state s2에서 Every-Visit MC의 V의 예측값은 무엇인가?
First-Visit의 경우 각각 첫 번째 s3, s2, s1에서만 Value를 예측하고,
𝛾=1이므로 V(s1) = 1, V(s2) = 1, V(s3) = 1, 그 외 나머지 state에서는 V(s)는 0이 될 것이다.
Every-Visit의 경우도 이와 마찬가지이다.
V(s1)=1이고, s2는 두번 나오지만 V(s) = G(s) / N(s) 이므로 2/2 = 1, 즉 V(s2) = 1이 된다.

이를 아까 DP처럼 트리형 구조로 나타낸다면,
DP는 맨 위에서만 Bootstrapping을 하던 반면,
MC는 가능한 경우의 수를 샘플을 내어 평균을 내서
그 값을 reward의 예측값으로 사용하게 된다.

Monte Carlo방식의 한계점들은 다음과 같다.
- 일반적으로 variance가 높은 편이다. 이를 줄이기 위해선 많은 데이터가 필요하다.
- episodic setting이 필요하다. episode가 끝나야지만 Vπ(s)가 update되기 때문이다.

다음은 MC의 요약본이다.
위의 내용을 잘 숙지하고 넘어갈 수 있도록 하자.

다음으로 배울 내용은 TD learning이다.
이 방식은 위의 Monte-Carlo 방식과 비슷하게 Model이 필요없다.
또, DP와 같이 Bootstrap 하면서도 MC와 같이 sample을 내기도 하며,
episodic하건 infinite-horizon / non-episodic 하건 사용가능하며,
각각의 (s, a, r, s') (state, action, reward, next_state) 튜플이 지나갈 때 마다 V의 예측값을 업데이트 해 준다.
(각각의 time step마다 update한다는 뜻)

저번 시간에 잠깐 했던 벨만 방정식 (Bellman operator)을 다시 가져오자면,
Vπ(s) 는 현재 immediate reward r(s, π(s)) 와 discounted sum의 합이었다.
그리고 every-visit MC에서, Vπ(s) = Vπ(s) + α(Gi,t - Vπ(s)) 라고 정의했었다.
이 때, Gi,t를 계산하기 위해선 episode 하나를 통째로 끝날 때 까지 기다려야 했다.
그런데, 그냥 이 Gi,t를 Bellman operator로 바꾸어서, rt + 𝛾Vπ(st+1)라고 두면 어떨까?
즉, DP와 같이 다음 reward를 계산할 때, 이미 갖고 있는 데이터를 바탕으로 계산하자는 것이다.
어렵게 생각할 것 없이, 그냥 저번에 했던 DP의 방식을 조금만 차용했을 뿐이라고 생각하면 된다.
실측값인 Gi,t는 state가 Markov 하다면 Bellman Operator와 동일하게 성립하지 않겠는가?

이것을 알고리즘으로 나타내면 다음과 같다.
α값을 input으로 준 뒤에, (내가 선택하면 된다.)
모든 state에 대해 Vπ(s) = 0으로 초기화 한 뒤,
(st, at, rt, st+1) 튜플을 샘플링 하여
이 튜플을 바탕으로, 아까 제안했던 TD 공식을 사용하여
Vπ(st) = Vπ(st) + α(rt + 𝛾Vπ(st+1) - Vπ(st)) 를 그대로 반복하는 것이다.

빠른 이해를 위해, 바로 예제로 들어가보자.
아까 전과 같이 Mars rover예제로, R = [1 0 0 0 0 0 10]이라고 가정하고
s1이나 s7에 도달하면 그 뒤에 무조건 episode가 terminate 된다고 하자.
이 때, (s3, a1, 0, s2, a1, -, s2, a1, 0, s1, a1, 1, terminal) 의 튜플이 주어질 때, (ppt 오른쪽 위에 쓰여진 대로 수행된다.)
α=1에서의 TD 예측치는 무엇인가?
이를 식으로 잠시 나타내어
Vπ(st) = Vπ(st) + α(rt + 𝛾Vπ(st+1) - Vπ(st))를 위 상황에 대입하면,
α, 𝛾 모두 1이므로
Vπ(st) = Vπ(st) + rt + Vπ(st+1) - Vπ(st)
= rt + Vπ(st+1)가 된다.
모든 state s에 대해 Vπ(st) = 0으로 초기화 했으므로,
Vπ(s3) = rt + Vπ(s2)
-> Vπ(s3) = 0 + 0 = 0
Vπ(s2) = rt + Vπ(s1)
-> Vπ(s2) = 0 + 0 = 0
Vπ(s1) = rt + Vπ(terminated)
-> Vπ(s1) = 1 + 0 = 1
즉, Vπ(s1)=1, 그 외 나머지 state 에서 Vπ(s) = 0이 된다.
이것이 TD Learning과 MC의 차이점인데,
MC의 경우 Vπ(s3)를 계산할 때 모든 경로를 끝까지 계산하여, s1에 도달했을 때의 그 값 또한 Vπ(s3)의 값에 넣어두지만,
TD Learning은 그냥 s3에서 s2로 한번 간 순간 이미 Agent가 s3에 있었다는 정보를 바로 버리게 된다.
그렇기 때문에 TD learning은 추후에 s1에 도달하더라도 s3의 값에는 변화를 주지 않는다.
그리고 그렇기 때문에 TD learning은 Monte Carlo와는 다르게 episodic 하지 않아도 되는 것이다.
어차피 끝까지 가지도 않고 바로 앞에서 무슨 일이 벌어지는지만 bootstrapping하여 알아내기 때문이다.
+ 위 경우엔, α=1이었기에 아무리 반복해도 딱히 변하지를 않았지만,
α=1이 아닌 경우엔, 지속적으로 반복하면 Vπ(s2), Vπ(s3)의 값들도 조금씩 변화하며
계속 반복하게 되면 일정 값에 수렴하게 될 것이다.
가령, α=2의 경우엔,
Vπ(st) = Vπ(st) + 2 * (rt + Vπ(st+1) - Vπ(st))
= 2 * (rt + Vπ(st+1)) - Vπ(st) 가 된다.
이 때는 Vπ(st)의 값들이 어떻게 바뀌는지는, 직접 해보며 익히길 바란다.
++ 참고로, α=1인 경우의 TD update Vπ(st) = rt + Vπ(st+1)는 TD(0)이라고도 한다!

이를 트리형 구조로 나타내면 다음과 나타낼 수 있다.
TD는 value를 예측하기 위해 st+1을 샘플링 하여 기댓값의 근사값을 찾아내고,
V(st+1)의 예측치를 활용하여 DP와 비슷하게 bootstrapping하여 value를 update한다.
일종의 MC와 DP의 짬뽕 느낌이 확 들지 않는가?

그럼, 이제부터 DP, MC, TD의 속성들을 비교해보자.
- model 없이 사용 가능한가?
우선, DP는 무조건 MDP가 필요한 방법이므로 X
MC, TD는 경우의 수를 샘플링 하는 방식으로 진행되므로, model-free하다. O
- non-episodic한 경우 사용 가능한가?
MC의 경우 episode 한번이 끝날때 마다 update하는 방식이므로, 무조건 episodic한 경우여야 한다. X
DP, TD의 경우 bootstrapping하여 Vπ(s)를 얻어내는 방식이므로, non-episodic / infinite episodic의 경우도 가능하다. O
- Non-Markovian할 때 사용 가능한가?
MC의 경우 그저 가능한 경우의 수를 나열하는 것이므로, Markovian하건 안하건 그냥 평균만 내면 되는 방식이다. O
DP, TD의 경우 state가 Markov하다는 전제 하에 bootstrapping을 하는 것이므로, state는 Markovian 해야 한다. X
- 극한값에서 실제 값에 수렴하는가?
DP, TD는 bootstrapping을 하면 할수록 수렴하고, MC의 경우도 episode를 무수히 반복하다 보면 큰 수의 법칙에 의해 수렴한다. O
- unbiased한가?
MC의 경우, First-Visit MC는 unbiased 하지만, Every-Visit MC는 biased하다. O
TD의 경우, bias가 있다고 할 수 있다.
가령 아까 위의 Check your understanding에서, α=2의 경우에 첫 번째 반복에선 Vπ(s1)만 reward가 1이라고 되는 편향이 생긴다.
(다르게 이야기하자면, s3, s2일 경우에 reward가 0이라는 편향값이 생긴다고 보면 될 것 같다. 즉, 정확하지 못하다는 것이다.)
DP의 경우가 제일 특이한데, Vπ(s+1)의 값은 Model을 통해 얻는 정확한 값이므로 Bias가 있다고 하기엔 애매한 감이 있다. NA

그리고, MC, TD 등의 알고리즘을 선택할 때 Bias/variance, Data efficiency, Computational efficiency와 같은 점들을 고려해야 한다.
(이 근방 부분은 나중에 더 자세히 다루겠다고 하신다.)

이번에 생각할 내용은 Batch (Offline이라고도 한다?) solution에 대한 내용이다.
K개의 finite한 episode가 있을 때, K에서 반복적으로 샘플링을 해서 MC 또는 TD(0)의 방식을 적용할 때,
MC와 TD(0)은 어떻게 수렴할까?
* TD(0)은 α=1일 때의 TD를 의미함.

다음 예시를 보도록 하자.
𝛾=1이라고 가정하자.
오른쪽 위의 노드 그림과 같은 State가 있다.
다음과 같은 8개의 에피소드가 존재한다;
- A, 0, B, 0
- B, 1 (6번 반복)
- B, 0
(이 때, A,B는 state, 0,1은 reward를 의미한다.)
이 때, MC와 TD(0)방식의 V(A), V(B)는 어떻게 수렴할까?
우선 V(B)부터 보도록 하자.
MC를 사용하면, 결국 B는 8번의 episode가 존재하고 그중 6개의 episode에서 1의 reward를 받았으므로,
V(B) = 6/8 = 3/4가 될 것이다. (무한히 많이 반복하면 이렇게 수렴하게 된다는 뜻이다!)
TD(0)를 사용하더라도 결국 sampling 후 무한정 bootstrapping하다 보면, 6/8 = 3/4로 수렴하게 될 것이다.
하지만, V(A)의 경우는 조금 다르다.
MC를 사용하게 되면, A는 언제나 A, 0, B, 0으로 갔으므로, V(A) = 0이라고 생각할 것이다.
(이 episode 들 중 A에서 출발하는 경로는 단 하나이고, 언제나 0의 reward를 뽑아냈기 때문이다.)
하지만 TD(0)를 사용하게 되면, 이야기가 조금 달라지게 된다.
TD(0)에서 사용했던 공식을 다시 한번 가져오자면,
Vπ(st) = rt + 𝛾Vπ(st+1) 였고,
𝛾=1이라고 했으므로 Vπ(st) = rt + Vπ(st+1)이 된다.
즉 Vπ(A) = rt + Vπ(st+1)
= 0 + Vπ(B)
= 0 + 3/4
= 3/4
그러므로 MC를 사용했을 때의 V(A) = 0, TD(0)을 사용했을 때의 V(A) = 3/4라는, 다른 값이 나오게 된다.

이것을 통해 MC와 TD가 Batch setting에서 수렴하는 방식의 차이를 알 수 있다.
MC의 경우는 MSE (Mean Squared Error)를 최소화하는 방식으로 수렴하게 되어,
이미 관찰된 return에 대한 오차를 최소화하는 방식이다.
TD(0)같은 경우, MDP에 최대한 가깝게 수렴하는데,
가령 P(B|A) = 1이고, r(B) = 3/4, r(A) = 0이므로 V(A) = 3/4라고 예측하는 것이다.
(이는 TD가 Markov structure을 사용하기 때문이다. MC는 Markov structure가 아니기에, MSE만을 최소화한다.)
여기까지 CS234 3강의 내용이었다.
쓰다보니 엄청나게 길게 쓴 것 같다.
여기까지 읽는 사람은 없을 것 같아서 쓰는 말이지만,
통계학 공부를 조금 더 하고 나서 인공지능을 다시 배워야될 것 같은 걱정이 들기 시작한다.
게다가 죄다 영어로 써져 있어서 직역해야 하는건지 수학 용어인지도 모르는 것들이 쑥쑥 나와서
다른 강의보다 더 쓰기 힘들었던 것 같다.
아무튼 다음 CS234 4강에서 보도록 하자.
수고링 ㅎ
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |
| 강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란? (5) | 2019.04.06 |
CS234 Assignment 1 해석
CS234의 Assignment1의 해석입니다.
사실 풀이까지 쓰려고 했는데, 학교에다가 노트를 두고오는 바람에... 풀이는 나중에 사진으로 대체하겠읍니다..
한번 풀어보시기 바랍니다. 재밌음 ㅎㅎ
아래 Assignment의 pdf와 코딩 문제의 파일은 CS234 assignment 페이지 (http://web.stanford.edu/class/cs234/assignment1/index.html) 에서 다운로드 받을 수 있습니다.

1. Figure 1에 있는 간단한 n-state MDP를 보자. State s1에서 시작하는 Agent는 어떤 state si에서도 오른쪽 (a0) 또는 왼쪽 (a1)으로 가는 action을 취할 수 있다. 모든 Action은 deterministic(결정론적)이고, 언제나 성공한다. (가령 s2에서 왼쪽으로 가면 s1으로 가고, s1에서 왼쪽으로 또 가면 s1 자신으로 돌아온다.) State에서 Action을 취함으로써 Reward를 취할 수 있다. goal state G에서 취한 모든 Action은 r(reward) += 1 을 얻고, G에 머무른다. 그 외의 나머지 행위는 reward 0을 얻는다. discount factor ᵞ < 1 이라고 가정한다.
(a) optimal action은 (최적의 action은) 어떤 state si에서든 G에 도달할 때 까지 오른쪽으로 가는 것이다 (action a0을 취하는 것이다). 이 때, 모든 state si와 goal state G에서의 optimal value function을 구하여라. [5점]
(b) optimal policy가 discount factor ᵞ의 영향을 받는지에 대해 서술하시오. [5점]
(c) 모든 reward 에 상수 c를 더한다고 생각해보자. (즉, G에서는 reward 1+c를, 나머지 state에서는 reward c를 받는다.)
이 때, 모든 si와 G에 대한 새로운 optimal value function을 구하시오. 상수 c를 더한 것이 optimal policy를 바꾸는가? 답을 설명하시오. [5점]
(d) 모든 reward에 상수 c를 더하고 상수 a를 곱한다고 해보자. (new_r = a * (c + old_r)) 이 때 모든 si와 G에 대한 새로운 optimal value function을 구하여라. 이것이 optimal policy에 변화를 주었는가? 답을 설명하고, 만약 '그렇다'고 답했다면 optimal policy를 바꾸는 a와 c의 예시를 드시오. [5점]

이번 문제에서는 value iteration을 사용하여 optimal policy를 찾을 때 사용할 steps의 갯수를 제한하는 예시를 들 것이다. Figure 2에 나오는 discount factor ᵞ < 1 인 infinite MDP를 보자. 이 MDP는 state 3개로 구성되어 있고, state에서 action을 취할 때 reward를 얻는다. state s0에서 a1의 Action을 취하면 0의 reward를 얻은 뒤 s1으로 이동하고, 그 이후의 모든 action에 대해 r = +1을 얻는다. state s0에서 a2의 Action을 취하면 s2로 이동하고 즉시 ᵞ^2 / (1-ᵞ) 의 reward를 얻지만, s2는 그 이후의 모든 action에 대해 r = +0을 얻는다.
(a) time step t=0인 state s0에서 action a1을 취할 때, 최종 discounted return (위 수식 참고)은 무엇인가? [5점]
(b) time step t=0인 state s0에서 action a2를 취할 때, 최종 discounted return (위 수식 참고)은 무엇인가? optimal action은 무엇인가? [5점]
(c) 모든 state의 value를 0으로 초기화 했다고 가정하자. value iteration은 위의 수식 (n* ≥ log(1-ᵞ)/logᵞ ≥ 1/2 * log(1/1-ᵞ) * 1/(1-ᵞ)이 성립할 때 까지 sub-optimal action을 선택하는데, 이를 증명하여라.
따라서, value iteration은 1/(1-ᵞ)보다 빠르게 증가한다. (첫 번째 부등식이 옳다는 것만 보이면 된다.) [10점]

finite MDP M = <S, A, T, R, ᵞ> 가 있다고 생각해보자. (S = state space, A = action space, T = transition probability, R = reward function, ᵞ = discount factor이다.)
Q* 을 optimal state-action function인 Q*(s, a) = Qπ*(s, a) (이 때, π*는 optimal policy이다.) 라고 정의하자.
또, ||x||∞ = max(|x(s, a)| 일 때 Q* 의 예측값인 Q˜을 가지고 있다고 가정하자. (이 때 Q˜는 l∞ norm ||Q˜ - Q*||∞ ≤ ε으로 제한되어 있다.)
만약 Q˜에 대한 greedy policy, π(s) = argmaxₐ∈AQ˜(s, a)를 따른다고 가정하자. 이 때, 우리는 다음을 보이고 싶다: Vπ(s) ≥ V*(s) − 2ε / (1 − γ)
(이 때 Vπ(s)는 π에 대한 greedy policy를 따르는 value function이고, V*(s) = maxₐ∈AQ*(s, a)는 optimal value function이다.)
이것은 만약 우리가 거의 optimal한 state-action value function을 계산하여 그 대략의(approximate한) state-action value function에서 greedy policy를 뽑아낸다면, 그 policy는 실제 MDP에서도 잘 작동한다는 것을 보여준다.
(a) π*가 optimal policy이고 V*이 oprimal value function이라고 하고, 위에서 정의했듯 π(s) = argmaxₐ∈AQ˜(s, a)라고 하자. 모든 state s∈S에서 다음의 부등식, V*(s) − Q*(s, π(s)) ≤ 2ε을 만족함을 보여라. [10점]
(b) part 1의 결과를 사용하여, Vπ(s) ≥ V*(s) − 2ε/(1−γ)임을 증명하라. [10점]
이렇게, 위의 범위가 성립함을 보였다. figure 3에 나온 2-state MDP를 고려하자. 이 MDP의 state1은 두 가지 action이 가능하다. 첫 번째 action은 reward 0을 얻고 다시 자기 자신의 state s1으로 돌아로는 action이고, 두 번째 action은 reward 2ε를 얻고 state s2로 가는 action이다. state s2는 추후의 모든 time step에 대하여 reward 2ε를 얻으며 자기 자신으로만 갈 수 있다. (어떤 action을 취해도 reward 2ε를 얻고 state s2로 돌아온다.)
(c) 모든 state에 대하여, optimal value function V*(s)를 구하고, state s1와 각각의 action에 대한 optimal state-action value function Q*(s, a)를 구하여라. [5점]
(d) π(s) = argmaxₐ∈AQ˜(s, a)일 때, Vπ(s1) − V*(s1) = −2ε/(1−γ)를 만족시키는, (l∞ norm으로 측정된) ε error를 갖는 대략적의 state-action value function Q˜이 존재함을 보여라. (일관적인 tie break rule을 정의해야 할 수도 있다.) [10점]

이제 OoenAI Gym을 사용하여 Frozen Lake environment에 대한 value iteration과 policy iteration을 구현할 것이다.
starter code 에 이 environment의 custom version을 제공하였다. (최상단의 링크에서 다운로드 가능)
(a) (코딩 문제) vi_and_pi.py를 읽고, policy_evaluation, policy_improvement, policy_iteration을 구현하라.
maxₛ |old_V(s) - new_V(s)|로 정의되는 stopping tolerance는 10⁻³이고, γ=0.9이다. optimal value function과 optimal policy를 return하여라. [10점]
(b) (코딩 문제) vi_and_pi.py에서 value_iteration을 구현하여라. stopping tolerance는 10⁻³이고, γ=0.9이다. optimal value function과 optimal policy를 return하여라. [10점]
(c) 각각의 방법 (vi와 pi)를 Deterministic-4x4-FrozenLake-v0과 Stochastic-4x4-FrozenLake-v0의 environment에서 실행시켜 보아라. 두 번째 environment에서, world의 dynamics는 무작위적이다. (world가 어떻게 움직이는지 랜덤이라는 뜻이다.) 이 무작위성은 반복의 횟수와 policy의 결과에 어떤 영향을 미치는가? [5점]
이해가 잘 되지 않는 부분이 있거나, 혹시라도 제가 잘못 해석한 부분이 있다면 댓글로 시정 요청 부탁드립니다.
(풀이는 나중에 올리도록 하겠습니다!)
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
| CS234 Assignments 1-1 Solution 및 풀이 (0) | 2019.04.25 |
강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP

- 본 포스팅은 CS234 2강의 내용을 정리합니다.

CS234 2강의 주요 내용은
- Markov Process (+ Markov Chain)
- Markov Reward Process (MRP)
- Markov Decision Process (MDP)
- Policy Iteration (PI)
- Value Iteraion (VI)
등이 있습니다.

Markov Process
Markov 한 상태를 띄는 랜덤한 State들.
Action도 없고, Reward도 없는 상태이다.
S는 states의 유한집합이고,
P는 현재 state s에 대해 다음 state s'를 나타내는 dynamics/transition model이다.
+ P는 그냥 모델이라는 뜻으로 받아들이면 된다. 단, 원래 모델에서의 정의와는 달리 다음 state인 st+1이 action에 영향을 받지 않고 이전의 state만의 영향을 받는다.
그리고, 이것을 Matrix로 하여 나타낸 것이 Markov Chain이다.
(아래쪽에 있는 Matrix)


Markov Reward Process (MRP) - Markov Process에 reward를 추가함.
S,P의 정의는 같고,
R는 reward function인데,
reward function은 현재 state에 대한 reward의 기댓값을 표현하는 함수이다.
ᵞ(감마)는 [0,1]의 범위를 갖는 discount factor이다.
discount factor는 현재 얻을 수 있는 immediate reward와 나중에 얻을 수 있는 reward간의 차이를 의미한다.
(나중에 더 자세히 나옴)
여기서도 Markov Process와 같이 Action은 없다.

Horizon : 각각의 에피소드에 대한 time step의 개수.
Agent나 Process의 time step의 개수.
horizon이 무한하지 않으면 finite Markov reward process라고 불리지만,
많은 경우 무한하다.(infinite)
가령, 주식 시장은 오늘도 열리고 내일도 열리고 모레도 열리고 .... 하는 식이다.
(그러니까 여기서 말하는 infinite는 엄밀한 정의의 infinite가 아니라, 그만큼 엄청 많아서 무한하다고 불러도 될 정도를 의미한다. 주식 시장은 사실상 우리가 살아있는 동안은 열려 있지 않겠는가? 그런 식이다.)
Return function (Gt) - time step t부터 horizon까지의 reward의 discounted sum.
즉, 지금부터 이 process가 끝날 때까지 (horizon이 무한하다면 그냥 앞으로 쭉)의 reward에 discount factor ᵞ를 곱한 값의 합.
State Value Function (V(s)) - state s에서 얻을 수 있는 reward의 기댓값.
참고로, 위 수식은 앞으로 계속 나오므로 잘 숙지해 둬야 한다!
Return function은 실제로 얻는 reward를 의미하고, Value Function은 그 reward의 기댓값이므로, 서로 다를 수 있다.
(물론, Deterministic한 경우엔 같을 수도 있다.)
위의 수식을 보면 알겠지만, V(s)는 state s일 때의 Gt의 기댓값으로 나타낼 수 있다.

Discount factor은 immediate reward (즉각적 보상)과 future reward (미래에 얻을 보상)과의 연관관계를 나타낸다.
[0, 1]의 범위 안에서, ᵞ = 0이면 future reward 무시, ᵞ=1이면 immediate reward = future reward란 의미를 가진다.
이때 ᵞ를 사용하는 것은 infinite 한 value를 피할 수 있으므로 수학적으로 용이하지만,
horizon이 finite한 경우에는 ᵞ=1을 사용해도 어차피 infinite한 value는 나오지 않으므로 ᵞ=1을 사용할 수 있다.

s1일때 reward 1, s7일때 reward 10, ᵞ=0.5라고 하자.
s4에서 시작해서 s5,s6,s7으로 가면
V(s)의 수식대로 갔을 때,
V(s) = 0 + 0.5 * 0 + 0.25 * 0 + 0.125 * 10 = 1.25
가 된다.
(이해가 안되면 저 위에 있는 V(s)의 공식을 보고 오라.)
그 외의 경우는 위의 ppt를 보며 직접 확인하면 될 것 같다.
V = [1.53 0.37 0.13 0.22 0.85 3.59 15.31] 은 각각의 s값에 대한 V(s)의 값이다.

MRP를 계산하는 방법은 크게 세 가지가 있다.
그 중 첫번째가 simulation인데,
그냥 하나하나의 경우의 수를 다 해보는 것이다.
(s4, s5, s6, s7의 경우, s4,s4,s5,s4의 경우 등등 그냥 죄다 해보면서 확률적으로 값을 도출한다는 뜻.)

두 번째 방법은 수학적인 방법이다.
finite state MRP의 경우, V(s)를 Matrix 연산으로 표현 가능한데,
V(s1, s2, ..., sn)은 각각의 state의 Reward (immediate reward)에 가능한 모든 경우의 수 (Markov Chain)에 Discount factor ᵞ를 곱하고, 거기에서 각각의 V(s1, s2, ..., sn)의 값을 또 곱한 것으로 표현이 된다.
(여기서 다시 곱하는 V(s1, s2, ..., sn)은 action을 취한 이후의 지점의 s값을 따른다. 밑의 예시를 참고하자.)
가령, 위의 Mars Rover MRP의 예시를 가져온다면
ᵞ가 0.5일때,
V(4)는 ᵞ(0.5)에다가 s4가 취할 수 있는 모든 경우의 수인 가만히 있기 (0.2), 왼쪽으로 가기 (0.4), 오른쪽으로 가기 (0.4)를 곱하고, 그 각각의 state의 V(s)를 곱해준다. (V(3), V(4), V(5))
더 자세한 예시는 밑에 나온다.

세 번째 방법은 Dynamic Programming이다.
k=1부터 시작해서, 모든 s에 대하여
Vk(s) = R(s) + ∑ᵞP(s'|s)Vk-1(s')를 계산해준다.
(이를 |Vk - Vk-1| < ε(엡실론, 그냥 아주 작은 특정 값) 일때 까지 반복한다.)
(그냥 저 V(s)의 공식을 다이나믹 프로그래밍으로 계산한다는 뜻이다.)

Markov Decision Process (MDP) : Markov Reward Process (MRP) + action
즉, MDP란 MRP에 action이 추가된 최종 진화형이다.
이게 어차피 Markov 변화의 마지막 형태이니까 기호를 하나씩 다시 써보면...
S는 Markov State s의 집합.
A는 actions 의 집합.
P는 각 action에 따른 dymanics/transition model. (위의 MRP / MP와 다르게 action이 포함되었다.)
R은 Reward function으로, 각 state와 action에 따른 reward의 기댓값이다.
그래서, MDP는 이 S,A,P,R과 discount factor ᵞ를 포함한 튜플 (S, A, P, R, ᵞ) 로 표현 가능하다.

위의 사진은 MDP에서의 P의 예시이다.
a1은 왼쪽으로 갈 확률이 1인 (즉, 무조건 왼쪽으로만 가는) action의 집합이고
a2는 오른쪽으로 갈 확률이 1인 (즉, 무조건 오른쪽으로만 가는) action의 집합이다.

Policy : 각각의 state에서 어떤 action을 취할지를 선택하는 것. (그냥 말 그대로 정책이다.)
결정론적(deterministic)일 수도, 확률적(stochastic)일 수도 있다.
Policy는 π(a|s) 이고, 이는 P(at = a | st = s) 와 같다.

그리고, MDP + π(a|s)는 Markov Reward Process 로 유도할 수 있다.
(정확히는, MRP(S, Rπ, Pπ, ᵞ) 로 유도할 수 있다.)
왜냐하면, π(a|s) 그 자체로 어떤 action을 취할지 알려주는 것이므로,
결국 π(a|s)만 알면 그 policy에 대한 reward의 기댓값 Rπ도 도출되고,
취할 행동의 distribution인 Pπ도 도출되는 것이다.
MDP는 MRP에서 R과 P를 Action에 관한 것으로 변경한 것이고,
policy는 각각의 state에 따른 action을 mapping 한 것이므로 (action을 대체 가능하다.)
MRP에서 R, P를 각각 Rπ와 Pπ로만 바꿔주면 되는 것이다.
이 성질은 추후 evaluation을 할 때 MDP가 아닌 MRP만 사용하면 되게 해주는 장점을 갖는다.

즉 위의 MDP + π(a|s) = MRP라는 성질을 사용하면
아까 저기 위에 있던 MRP의 Dynamic programming 수식을 조금만 바꾸어서,
Policy에 대한 V(s)를 구할 수 있게 된다.
(수식 참고)

위의 경우를 보자.
Mars Rover (로봇) 은 왼쪽 또는 오른쪽으로만 갈 수 있다.
s1에 Mars Rover가 위치하면 reward +1, s7에 Mars Rover가 위치하면 reward +10을 주고,
그 외의 나머지 경우에는 reward는 0이 주어진다.
π(s)는 모든 state에 대하여 a1이고 ᵞ=0이라고 했을 때,
Dynamic Programming 방식을 기용한다면 policy의 value는 무엇일까?
답은, s1과 s7에 있을 때를 제외하면 죄다 0이고,
s1에 있을 때는 1, s7에 있을 때는 10이다.
어차피 ᵞ = 0이므로 위의 v(s) 의 식의 ᵞ의 뒤에 있는 식들은 죄다 날라가고,
π(s) 당시의 reward, 즉 immediate reward만 합해주면 되므로
s1에 있을 땐 1, s7에 있을 땐 10이다.

두 번째 문제이다.
P(s6 | s6 , a1) = 0.5, P(s7 | s6,a1) = 0.5 이고,
reward는 위와 같을 때,
π(s) 가 언제나 a1을 취하고 k=1, ᵞ=0.5일때 π(s6)의 reward는?
아까 전의 MRP로의 식을 사용하면 된다.
우선 immediate reward는 0이다. (s6의 reward는 0이므로...)
그리고, P(s6 | s6 , a1) = 0.5, P(s7 | s6,a1) = 0.5이고 ᵞ=0.5이므로 최종 계산식은
0 + ᵞ * 0.5 * v(s6) + ᵞ * 0.5 * v(s7)
= 0 + 0.5 * 0.5 * 0 + 0.5 * 0.5 * 10
= 2.5
가 된다.

MDP Control은 optimal한 policy를 compute한다.
즉, Vπ(s)가 최대가 되는 π의 값을 구하는 것이다.
그리고, optimal한 value function은 언제나 unique 하다. (교수님이 이 부분은 설명을 안하고 넘어가셨다.. 중요하다고만 하심)

아까 전의 Mars Rover의 예시를 다시 가져오자.
states는 s1부터 s7까지 7개의 state가 있고, action은 왼쪽 또는 오른쪽 두 가지만 있다.
이 때, deterministic한 policy는 몇개인가?
ppt에 적혀있듯, 2^7개이다.
(각각의 action 2개가 각각의 state에서 실행 가능하므로)
그리고 이 이후의 예제에서도,
action의 개수 A와 state의 개수 S에 대하여 가능한 policy의 개수는 A^S개이다.
그리고, MDP의 optimal policy는 언제나 unique 한가?
위의 ppt에서 적혀있듯, No 이다. 만약 다른 Policy 두개의 Value가 모두 optimal value function의 값이 된다면,
이 Policy들 모두 optimal policy가 된다.

Policy Search : Optimal한 policy를 찾는 과정.
Policy Iteration은 이의 한 종류이다.
i=0으로 설정하고, π0(s)를 랜덤한 값으로 설정한 뒤 시작하는데,
i==0 or |πi - πi-1| >0일 때 반복한다.
(시작할때와 policy가 바뀌고 있을 때 반복한다.)
그런데, 이것을 제대로 하려면 일단 Policy Improvement가 뭔지 알아야 한다.

일단, PI에 들어가기 전에 먼저 Qπ에 대해 알아보자면,
Qπ(s, a) = R(s, a) + ᵞΣP(s'|s, a)Vπ(s') 이다.
이는 Vπ(s , π(s|a)) 에서 R(s, π(s))를 R(s, a)로 바꿔준 식으로,
일단은 Policy를 따르지 않고 action a를 취한 후에
그 뒤에 policy를 따르겠다는 뜻이다.

그리고, Qπi(s, a)를 모든 State의 s, 모든 Action의 a에 대하여 compute한 뒤에,
모든 State에 대하여 Qπi(s, a)가 최대가 되는 π를 찾는다.
자, Qπi(s, a)는 π(s|a)를 그대로 따르는 것이 아니라 각각의 State에서 가능한 모든 Action을 취하는 것이므로...
Qπi(s, a)의 값들 중 최소한 하나는 π(s|a)보다 크거나 같을 것이다.
(각각의 State에서 가능한 모든 Action은 π(s|a)에서 취한 행동도 포함하므로, 무조건 같은 것 하나는 나오게 된다.)
그리고, 이것을 πi+1에 넣어준다.
이것을, Policy Improvement라고 한다.

그러면, 이제 위에서 무슨 말을 하는지 이해가 될 것이다.
| πi - πi-1 | == 0이라는 것은 결국 πi가 optimal 하다는 뜻이므로 |πi - πi-1| > 0 일때 동안 반복하는 것이고,
그렇게 나온 πi+1로 policy improvement를 해주고, i++을 해준다.
(이렇게 해도 이해 안되면 강의 보쉬던지... 깔깔!)

조금 더 깊게 파고들자면,
Qπi(s, a)의 Max값은 R(s, Vi(s)) .... (이하 Vπ(s))보다 언제나 크거나 같다.
그리고, πi+1(s) 는 Qπi(s, a)의 최댓값을 보장하는 a를 의미한다. (즉, 더 나은 policy가 된다.)
그리고는, 이 이후에는 πi+1을 가져가고, πi는 버린다.
πi+1은 언제나 πi보다 낫거나 같기 때문이다.

즉, 모든 State s에 대해 Vπi >= Vπ2 : Vπ2(s) >= Vπ2(s)라는 이야기이다.
이를 증명 하자면...

위의 수식처럼 된다.
약간 참고만 하라고 첨언하자면,
πi+1 = argmax(a)Qπi(s,a) 이다.
그리고 주목해야할 부분은 두번째줄에서 세번째 줄로 넘어가는 부분인데,
Vπi(s) <= max(a) Qπi(s, a)이므로,
Vπi(s') <= max(a) Qπi(s', a) 이라는 점에서 두 번째 줄에서 세 번째 줄로 넘어갈 수 있다.
이를 계속 반복하다 보면, 결국 Vπi(s) <= Vπi+1(s) 라는 식이 나오게 된다.
(증명은 알아서 이해할 수 있도록 하자 ㅎ)

위 ppt의 조건대로라고 했을 때, (Policy Iteration을 사용할 때)
만약 Policy가 한번 바뀌지 않으면 앞으로도 바뀌지 않는가?
PI에서 최대 반복 횟수가 있는가?
답은 위에서 확인하도록 하자. (설명도 잘되어 있다.)
첫 번째 질문에 대한 comment만 달자면, 한번 Policy가 바뀌지 않으면
| πi - πi+1 | == 0이 되므로
더이상 Policy Iteration이 진행되지 않는다.
그러므로, Policy도 더이상 변하지 않는다.


다음은 Value Iteration이다.
위의 Policy Iteration과 비슷하다고 느껴질 수 있지만, 조금 다른 방식이다.
V0(s)를 0으로 초기화 한 뒤에,
V가 어떤 값으로 Converge 될때 까지 (수렴할때 까지), 또는 horizon이 끝날때 까지
Vk+1(s) = max(a) R(s, a) + ᵞΣP(s'|s, a)Vk(s')
을 반복한다.
풀어 말하자면, 각각의 time step에 대해서 최선의 선택만을 가지고 가는 것이다.
이는 원래 Policy를 랜덤으로 취한 뒤 policy를 가장 좋은 것으로 바꾸어 가는 Policy Iteration과는 다른 방식으로,
처음의 time step 0으로 시작해서, 모든 state에서 가능한 최선의 action만을 취해서 Policy를 만들어 가는 것이다.

그리고, Value Iteration은 수렴하는가? 에 대한 답은 YES이다.
결국 V(s)의 값에는 지속적으로 ᵞ가 씌워지므로,
Horizon이 무한하더라도 1보다 작은 ᵞ값을 무한정 제곱하여 더하는 꼴이 되므로
일정한 값에 수렴하게 된다.

Value Iteration과 Policy Iteration간의 차이점을 설명하자면,
Value Iteration은 time step (horizon) = k일 때의 optimal value를 찾아가며 k를 증가시키는 형식이고,
Policy Iteration은 infinite한 horizon에서 더 나은 policy를 찾아가는 형식이다.
이 Policy Iteration은 RL에서 매우 유명한 Policy Gradient라는 방식과 매우 유사하다.
여기까지 CS234 2강을 정리하도록 하겠다.
사실 그냥 간단한 정리노트만 쓰려고 했는데, 어찌어찌하다 보니 뭔가 강의 형식이 되어 버렸다.
그냥 정리 노트와 강의를 합쳐버리는 게 나을지도 모르겠다.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란? (5) | 2019.04.06 |
모두를 위한 딥러닝 (sung kim) lec4 - Multivariable Linear Regression (다변수 선형 회귀)

이번 포스팅에서는, Multivariable Linear Regression, 즉 다변수 선형 회귀에 대해서 알아보겠습니다.

일단 저번 시간까지 했던 내용들을 복습해 보겠습니다.
일반적인 Linear Regression의 Hypothesis는 H(x) = Wx + b였죠?
Cost function은 H(x) - y를 제곱해서 모두 더한 뒤 평균값을 내주는 것이었고...
Gradient Descent는 가장 적절한 (cost(W) 값이 가장 작은) W값을 찾아내는 알고리즘이었습니다.
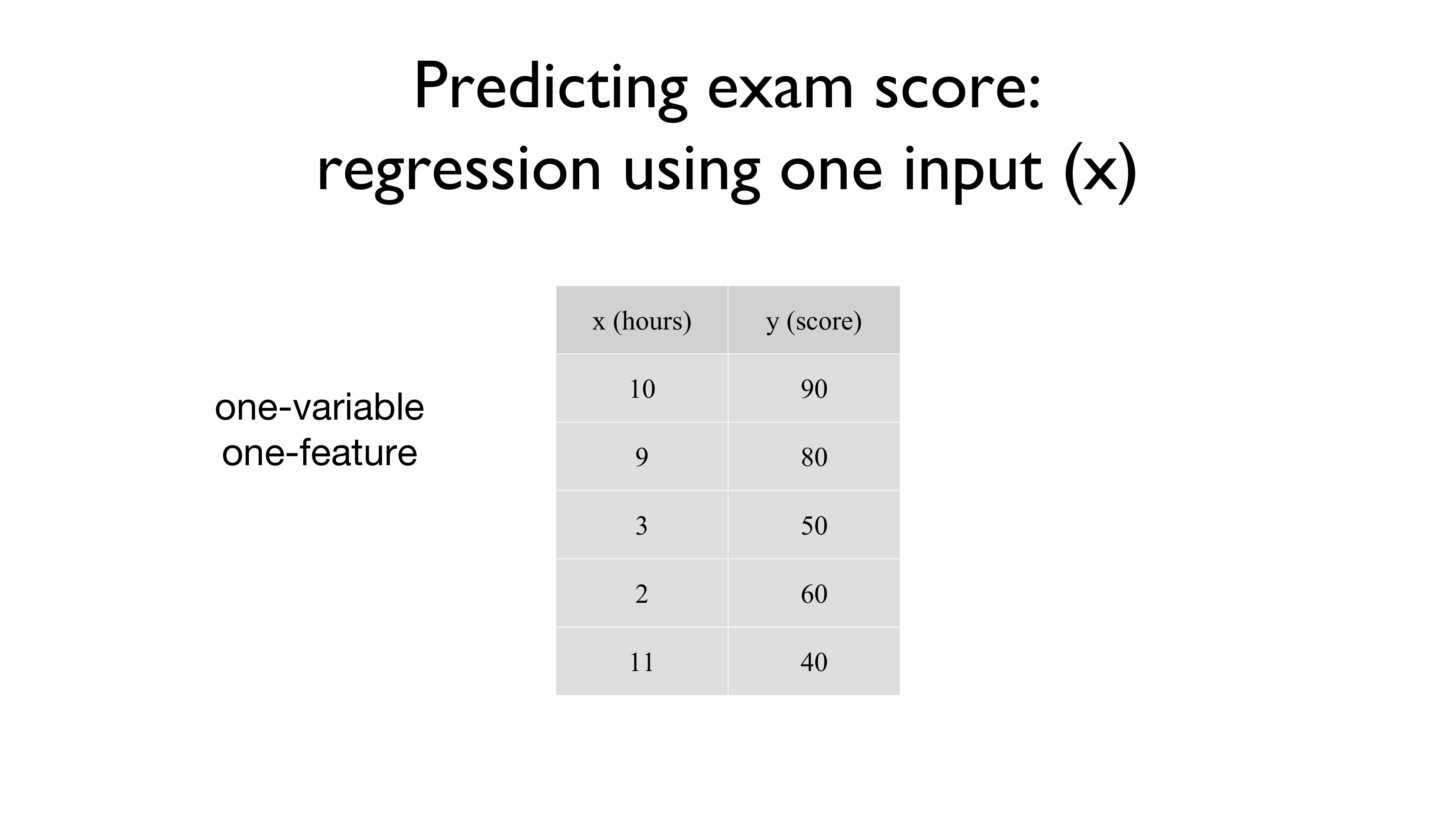
그리고 우리가 마주했던 데이터들은 다들 이런 형식으로 생겼습니다.
x값 하나당 y값 하나가 주어지는 형식이었죠.
이때, x는 하나의 feature을 의미합니다.
가령, 위의 경우엔 특정 점수 y를 그 점수를 갖게 되었던 특징인 feature x를 통해 알아봤던 것이죠.
그래서 위의 사진에서 one-variable one-feature라고 적혀있는 것입니다.
변수 하나에 특징도 하나밖에 (공부한 시간) 없으니까요.

그런데, 오늘 배울 Multi-variable Linear Regression은 데이터가 조금 다르게 들어옵니다.
x값이 하나가 아니라, 두 개, 세 개, 혹은 10000개도 들어오는데요,
각각의 x값 (x1, x2, x3)들은 각자의 특성을 띄고 있습니다.
위의 예시의 경우 x1 은 quiz1의 점수,
x2는 quiz2의 점수,
x3는 중간고사 1의 점수이고
이 점수들을 모두 어떠한 방식으로 계산했을 때 최종 점수인 Y가 나오게 되는 것입니다.

그런데, 그렇게까지 어려워지진 않았습니다!
Linear Regression의 기본형인 H(x) = Wx + b 를 그대로 따라서,
H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b
로 약간만 변형되었을 뿐입니다.
잠깐만 살펴보면, x의 종류 (feature의 개수)가 늘어나면, 그에 따라 w의 개수도 늘어나게 됩니다!
x1에는 w1, x2에는 w2, x3에는 w3를 곱해주는 식으로 말이죠.
그리고, b의 값은 여전히 그대로 남아있습니다.
feature가 많아졌다고 해서 b의 개수도 많아지진 않은 것이죠.
(그도 당연한 것이, 각자의 x값에 b를 더하더라도 어차피 상수 하나 더한 거랑 같으니까요.)

그럼, Cost function은 어떻게 바뀌었을까요?
H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b
를 그대로 우리가 사용하던 Cost function 안에 집어넣으면 됩니다.
즉, H(x1, x2, x3) - y 를 제곱한 것을 모두 더해서 평균을 내는 것이죠.
조금만 더 풀자면, H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b 이므로,
w1x1 + w2x2 + w3x3 + b - y 를 제곱해서 모두 더해주는 것이죠.

그리고 x1, x2, x3와 같이 feature의 개수가 세 개가 아니고 무수히 많더라도, 위의 식처럼
H(x1, x2, x3,... , xn) = w1x1 + w2x2 + w3x3 +... + wnxn + b
로 표현이 가능합니다.
즉, 우리가 원래 알고 있던 Linear Regression의 식을 아주 쬐끔만 변형시켜 주면,
Multi-variable Linear Regression도 뚝딱 해낼 수 있습니다.
그런데, 중요한 것은 그게 아니고,
"그래서 이거 계산 어떻게 할건데?"입니다.
그러니깐, 기본적인 Linear Regression에서는 x값이 10개 정도 주어지고, w값이 하나니깐
x1 * w + x2 * w + x3 * w +... + x10 * w + b
정도로 계산이 가능했고, 그냥 {x1, x2, x3,... , x10} * w + b만 해도 되었습니다.
하지만, feature이 많아져서, 상황이 조금 달라졌습니다.
x1의 첫 번째 데이터를 x11, x3의 네 번째 데이터를 x34... 이런 식으로 쓰고, feature가 n개이고 데이터의 개수가 m 개라면 우리가 계산해야 할 식은
x11 * w1 + x21 * w2 +... + xn1 * wn + b
+ x12 * w1 + x22 * w2 +... + xn2 * wn + b
...
+ x1m * w1 + x2m * w2 +... + xnm * wn + b
처럼... 딱 봐도 복잡한 이차원 배열 * 일차원 배열을 계산해야 합니다.
하지만, 이것을 반복문으로 그냥 쭉 돌려버릴 수도 없는 것이...
가령 n과 m이 각각 10 만씩이라고만 해도,
반복문으로 돌리면 100억 번의 연산을 해야 한다는 말도 안 되는 결과가 나오기 때문입니다.
그러면 이것을 어떻게 간단하게 연산할 수 있을까요?
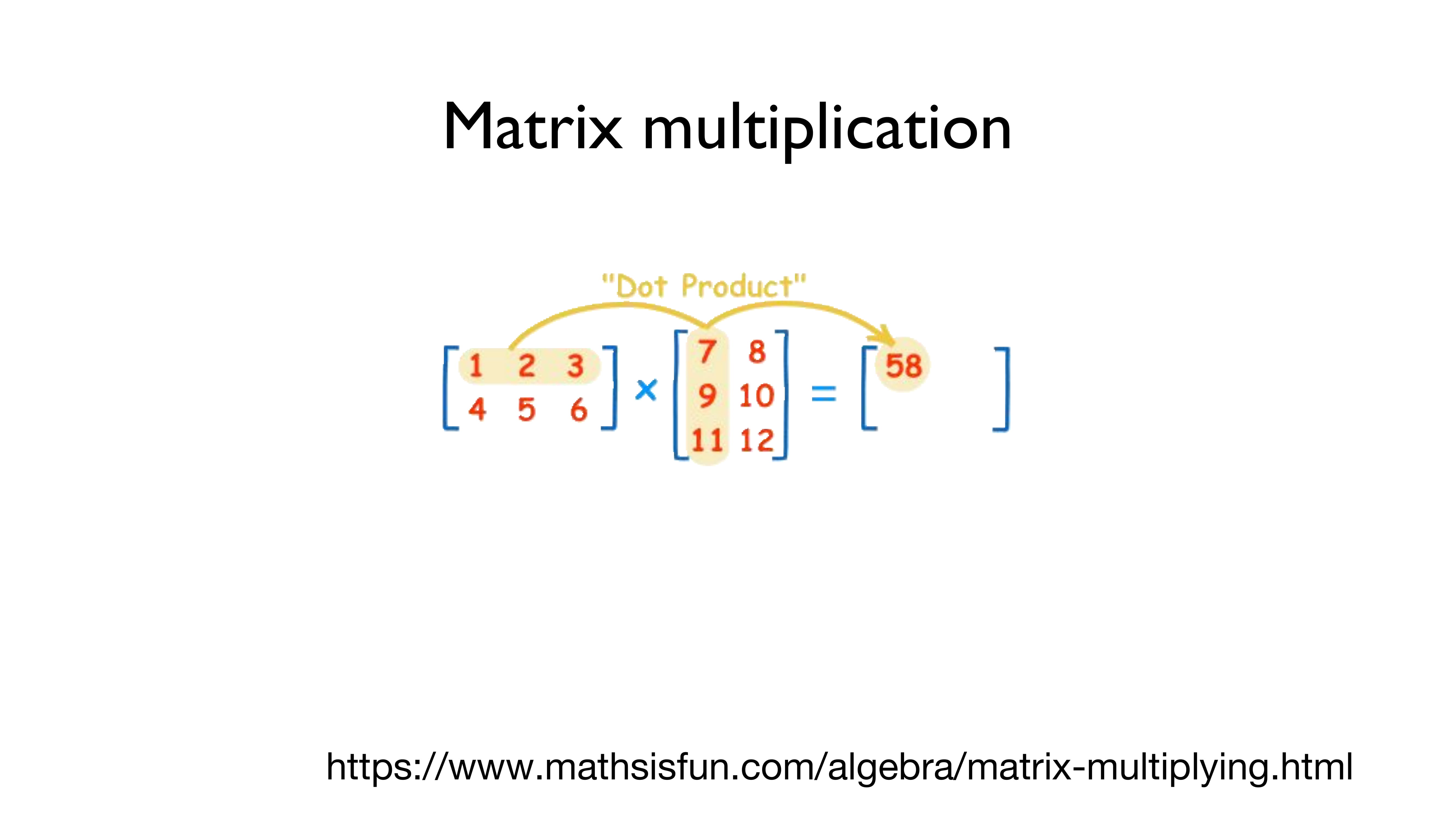
바로, "Matrix multiplication", 즉 "행렬곱"으로 이 문제를 해결합니다.
행렬곱은 어떤 식으로 진행되는지 위의 그림을 통해 알아봅시다.
(헷갈릴까 봐 써놓는데 - 가로가 행이고 세로가 열입니다!!!)
왼쪽의 [[1,2,3], [4,5,6]]의 (2,3)의 행렬과 [[7,8], [9,10], [11,12]]의 (3,2) 행렬을 곱하는 것은 간단합니다.
왼쪽의 행렬의 첫 번째 행인 [1,2,3]의 각각의 요소들을 오른쪽의 행렬의 첫 번째 열인 [7,9,11]로 곱해서 더해줍니다.
즉, 1*7 + 2*9 + 3*11 = 7 + 18 + 33 = 58
이 되는 겁니다.
그리고, 이 값을 결괏값의 행렬의 첫 번째 행, 첫 번째 열에 놓습니다.
두 번째도 동일하게 진행하면 됩니다.
왼쪽의 행렬의 첫 번째 행인 [1,2,3]의 각각의 요소들을 오른쪽의 행렬의 두 번째 열인 [8,10,12]로 곱해서 더해줍니다.
그러면, 1*8 + 2*10 + 3*12 = 8 + 20 + 36 = 64가 됩니다.
그리고, 이 값을 결괏값의 행렬의 첫 번째 행, 두 번째 열에 놓습니다.
두 번째 열은 직접 한번 해보시기 바랍니다.

자, 대충 배웠으니 한번 대충 적용해 봅시다.
w1x1 + w2x2 + w3x3을 행렬로 계산하려면 어떻게 해야 할까요?
x1, x2, x3를 (1,3)의 크기의 행렬로 놓고,
w1, w2, w3을 (3,1)의 크기의 행렬로 놓는다면,
행렬곱을 통해 x1 w1 + x2w2 + x3w3를 구할 수 있게 됩니다.

그런데, 우리가 가지고 있는 데이터는 x1, x2, x3값이 각각 하나만 들어있는 데이터가 아니죠?
x1 여러 개, x2 여러 개, x3 여러 개로 이루어진 데이터를 갖고 있는데, 이것을 어떻게 계산할까요?

아까 저 위에서 했던 짓을 똑같이 반복하면 됩니다.
우선, x값들의 행렬 중 첫 번째 행인 x11, x12, x13과 w1, w2, w3를 곱하여,
x11w1 + x12w2 + x13w3을 결괏값 행렬의 첫 번째 요소로 넣어줍니다.
그다음엔 x21w1 + w22w2 + w23w3 을 넣게 될 것이고,
그것을 마지막 데이터인 x51, x52, x53까지 반복하면 되는 것입니다.
그러면, 왼쪽의 x값의 데이터와 오른쪽의 w값의 데이터를 통해 결괏값을 행렬로 도출해 낼 수 있는 것이죠.

그런데 행렬곱에는 특징이 하나 있습니다.
입력되는 데이터의 형태에 따라 결괏값의 형태가 달라진다는 것이죠.
가령 바로 위의 예시를 보면, (5,3) 크기의 데이터와 (3,1) 크기의 데이터를 행렬곱하면, (5,1) 크기의 결괏값이 나오게 됩니다.
어떻게 보면 당연한 것이긴 합니다.
왼쪽의 (5,3) 행렬의 각각의 행을 오른쪽 (3,1)의 행렬에 곱해서 모두 더한 값은, 결괏값인 (5,1)의 행들에 집어넣고 있으니까요.
그런데, 여기서 중요한 점 하나가 더 있습니다!!
만약, (5,3) 크기의 행렬에 (2,1) 크기의 행렬을 행렬곱시키면 어떻게 될까요?
... 행렬곱 시킬 수 없습니다.. ㅎㅎ
이것도 어떻게 보면 당연한 것이겠지만,
x1, x2, x3를 w1, w2에만 곱할 수는 없는 노릇 아니겠습니까 ㅎㅎ
즉, 행렬곱을 계산해 줄 때에는 데이터의 크기를 잘 생각해야 합니다!
(n, m) 크기의 행렬을 x값으로 사용할 것이라면,
(m, 1) 크기의 행렬을 w값으로 사용해 주어야 한다는 것입니다.
그러면 결괏값은 (n, 1) 크기의 행렬로 나오게 되겠지요.

그런데, 중요한 게 또 또 있습니다!
행렬곱은 일반적인 곱셈과는 다르게 곱셈의 순서가 중요하다는 것입니다!
위의 식처럼, (5, 3) 크기의 행렬과 (3, 1)를 곱하면 (5, 1)이라는 행렬이 나오지만,
반대로 (3, 1) 크기의 행렬과 (5, 3) 크기의 행렬은 곱할 수 없다는 것입니다.
즉, 순서가 매우 매우 매우 중요합니다!!
앞 행렬의 행 크기와, 뒷 행렬의 열 크기가 동일해야 한다는 것입니다!
아까 전과 마찬가지로, (m, n)의 행렬에 곱할 수 있는 행렬은 (n , k) 꼴의 행렬뿐입니다.
(결괏값은 (m, k) 크기의 행렬로 나오겠죠.)



즉, 지금까지 하고 싶은 말이 무엇인고 하니...
우리가 Python이나 Tensorflow로 위의 Linear Regression을 구현하려면
지금까지 배웠던 H(x) = Wx + b 로 계산하는 것이 아니고,
H(X) = XW로 구현해야 한다는 것입니다!
이것을 특별히 더 강조한 이유는 간단합니다.
이거 처음 배울 때 저는 이 행렬 순서를 맞춰야 된다는 사실을 모른 채라 삽질을 오지게 했기 때문이죠 ㅎ
여러분들은 행렬의 크기를 맞추지 않아서 삽질하는 일은 없도록 합시다!

다음 포스팅에서는 Logistic Regression에 대해서 알아보겠습니다.
그럼 안녕!!
'인공지능 > 모두를 위한 딥러닝 (sung kim) lec' 카테고리의 다른 글
| 모두를 위한 딥러닝 부록편 - 미분의 개념과 Gradient Descent (1) | 2019.05.10 |
|---|---|
| 모두를 위한 딥러닝 (sung kim) lec5 - Logistic Classification (로지스틱 회귀분석) (0) | 2019.05.09 |
| 모두를 위한 딥러닝 (sung kim) lec3 - Gradient Descent (경사하강법) (0) | 2019.04.08 |
| 모두를 위한 딥러닝 (sung kim) lec2 - Linear regression & cost function (0) | 2019.03.30 |
| 모두를 위한 딥러닝 (sung kim) lec1 - 머신 러닝 기초 (0) | 2019.03.28 |
강화 학습 개념 정리노트 - CS234 1강 (강화 학습의 개념, MDP)

CS234의 강의를 바탕으로, 강화 학습의 개념을 정리합니다.
간단히 내용을 훑고싶은 분들에게 추천드립니다.
Reinforcement Learning (RL) - Learn to make good sequences of decisions
= 순차적 결정을 잘하도록 학습하는 것.
강화 학습이 다루는 측면 4가지
Optimization : 최적의 결정을 하도록 훈련하는 것.
Delayed Sequence : 지금 한 일이 나중에 영향을 미치는 것. ex) 미리 먹어둔 게임 아이템이 후반에나 쓰임.
Exploration : 새로운 일을 하도록 탐험하는 것. 이미 하지 않았던 것을 시도하며 관찰하는 것. ex) 한 번도 가지 않았던 길로 가봄.
Generalization : 훈련한 것을 일반화시키는 것. 픽셀값들로 훈련한 모델이라 하더라도, 조금 더 고수준으로 이해 가능하게 하는 것.
ex) 픽셀값으로만 훈련한 퐁 AI가 게임의 룰을 일반화해서 학습함.

Agent : 우리가 학습시키고자 하는 AI.
Action : 행동.
Observation : 관찰. Agent가 보고 듣는 것.
Reward : 보상. 어떤 Action을 취했을 때 얻는 점수의 개념임.
World : 세상. 일반적으로 학습시키고자 하는 환경을 의미함. (게임의 경우 게임 세상)
(저번 포스팅 복붙ㅎ)
강화 학습의 목표 - Agent가 최선의 Action을 취하도록 함.

History : 지금까지의 Observation의 기록
State : History를 활용하여 결정을 내릴 때 사용하는 정보
(State는 일종의 History를 이용한 함수임.)
World State : World를 구성하는 모든 것에 대한 State.
ex) 게임 규칙, 게임 진행 순서, 스테이지 개수 등등
Agent State : Agent가 볼 수 있는 World에 대한 State
ex) 게임 픽셀이 움직이는 방식
Markov Assumption : 충분한 정보의 State가 주어진다면, History 전체를 사용하여 예측한 결과와 그 State를 사용하여 예측한 결과가 같음.
즉, Markov Assumption이 참일때, 미래는 과거에 독립적임.
Markov Assumption의 사용 이유 : 일반적으로 어떤 경우에서라도 Markov Assumption을 참으로 만들 수 있음.
(State = History인 경우 언제나 만족함.)
Fully Observability : 완전 관찰가능함. World State를 모두 볼 수 있음. 이 경우, State = World라고도 함.
Partially Observability : 부분적으로만 관찰가능함. 위의 Fully Observability보다 일반적임.
이 경우, 관찰 가능한 부분에 대한 정보만을 갖고 결정을 내림.
ex) 포커 게임에서 상대방의 패를 보지 않고서도 게임을 진행함.
Bandits : 지금 취한 Action이 나중의 Observation에 영향을 끼치지 않는 문제류.
ex) 개별적인 고객에게 광고를 추천하는 것. (지금 무슨 광고를 제안해줘도 다음 고객이 왔을 때와는 별개임.)
MDP와 POMDP : 지금 취한 Action이 나중의 Observation에 영향을 미침.
전략적인 선택이 필요할 수 있음.
MDP의 종류
Deterministic(결정론적) - 특정한 상황에서 무조건적인 답이 존재함. (물리 문제와 같은 것.)
Stochastic(랜덤?) - 특정한 상황에서 무조건적인 답이 존재하지 않음. (광고를 추천해 줬을 때, 그 대상이 볼지 안 볼지는 모름.)
RL이 갖는 요소들 (안가질 수도 있지만, 최소한 하나씩은 가짐)
Model : Agent의 Action에 따라 어떻게 World가 변화하는지를 표현하는 것.
Policy : Agent가 어떤 상황에서 어떻게 Action 할지에 대한 정책.
Value function : Agent가 특정 Policy에 대해 얼마나 효과적인지 확인하는 함수.
Exploration : 탐험. 한번도 해보지 않은 짓을 하는 것. ex) 식당에서 먹어보지 않은 음식을 시킴.
Exploitation : 정답. 원래 제일 좋은 성과를 내던 짓을 하는 것. ex) 식당에서 맨날 먹던 것을 시키는 것.
Evaluation : Policy가 주어졌을때, 어떤 reward가 주어질지 예측하는 것.
Control - Optimization : 최선의 Policy를 찾는 것.
'인공지능 > 강화 학습 개념 정리노트 (CS234)' 카테고리의 다른 글
| 강화 학습 개념 정리노트 - CS234 2강 (MDP / MRP / Policy Iteration / Value Iteration) (0) | 2019.04.28 |
|---|
모두를 위한 딥러닝 (sung kim) lec3 - Gradient Descent (경사하강법)

안녕하세요.
이번 시간엔 머신 러닝의 꽃이라고 할 수 있는 Gradient Descent에 대해 알아봅시다.

저번 시간에 배웠던 내용을 잠시만 복습하고 들어가 봅시다.
우선, Linear Regression의 가설 함수는 H(x) = Wx + b 였고,
Cost function은 각각의 H(x) 값에서 y값(정답)을 빼준 후,
그 값들을 죄다 제곱해서 평균을 내주는 것이었습니다.
기억이 나지 않는다면, 이전 포스팅 (https://cding.tistory.com/12)에서 다시 한번 복습하고 와주세요!

그런데, 일단은 이해를 쉽게 하도록 하기 위해서 H(x)를 그냥 Wx라고 해봅시다.
(b를 빼준 것뿐, 일차함수라는 큰 틀은 변화하지 않았습니다.)
그러면, Cost function도 조금은 바뀌어서...
H(x)에서 y값을 빼주던 것을, Wx에서 y값을 빼주는 것으로 바꾸어도 상관없겠죠?
(H(x) = Wx 이므로)

그럼 이 상태에서 cost(W)의 값을 구해보도록 합시다.
X, Y가 왼쪽 표와 같이 주어진다면, 각각 W=1, W=0, W=2 일 때의 Cost값은 무엇일까요?
W=1일 경우,
X=1, Y=1에서 (W*x - y)^2 = (1 * 1 - 1)^2 = 0
X=2, Y=2에서 (W*x - y)^2 = (1 * 2 - 2)^2 = 0
X=3, Y=3에서 (W*x - y)^2 = (1 * 3 - 3)^2 = 0
이 세 가지 경우의 수를 모두 더하면 0+0+0 = 0, 평균으로 나눠도 0
즉, Cost(1) = 0입니다.
cost가 0이므로, W=1일 때 완벽하게 데이터에 들어맞는다는 뜻이죠.
W=0일 경우에는?
X=1, Y=1에서 (W*x - y)^2 = (2 * 1 - 1)^2 = 1
X=2, Y=2에서 (W*x - y)^2 = (2 * 2 - 2)^2 = 4
X=3, Y=3에서 (W*x - y)^2 = (2 * 3 - 3)^2 = 9
이 세 가지 경우의 수를 모두 더하면 1 + 4 + 9 = 14, 평균으로 나누면 14/3 = 4.66666...
즉, Cost(0) = 4.67입니다.
W=2 일 경우에는 어떨지, 직접 한번 해 보시길 바랍니다.
참고로, 답은 W=0일 때와 동일하게 4.67이 됩니다.

이렇듯, W값에 따라 cost(W)의 값은 변하게 됩니다.
W=1일 때 cost의 값은 0으로 최소가 되고,
W=2, W=0일 때 cost의 값은 약 4.67이 되는 식이죠.
이때, 이런 식으로 cost(W)에서 W의 값에 값들을 많이 집어넣게 되면 위의 그래프처럼 함수가 그려집니다.
(x축을 W로, y축을 Cost(W) 값으로 집어넣은 그래프입니다.)
위에서는 W=-3부터 W=5까지만 집어넣었지만, 다른 값들을 넣어도 여전히 이차함수의 그래프가 그려지게 되겠죠.
그런데, 어떻게 cost(W)의 값이 최소가 되는 W의 값을 구할 수 있을까요?

그래서 등장한 방법이 바로 Gradient Descent 알고리즘입니다.
(Gradient는 경사, Descent는 하강이므로 한국어로는 경사 하강법이라고 불립니다.)
위와 같은 상황에서 최소의 W값을 찾아주기 위한 알고리즘인데요,
굉장히 다양한 최소화 문제(특정 값을 최소화해주어야 할 때) 자주 사용되는 기법입니다.

일단은, Gradient Descent의 작동 방식에 대해 간단하게 먼저 알아봅시다.
우선, W를 랜덤 한 값으로 정해줍니다. (무엇으로 정해도 큰 상관은 없습니다.)
그런 후, 그 W의 값을 cost(W)의 값을 최소화시킬 수 있는 방향으로 바꿔줍니다. (보통 W값을 업데이트해준다고 표현합니다.)
그리고, 이 짓거리를 cost(W)가 최소가 될 때까지 반복합니다.
(저 위의 예시의 경우, W=1이 될 때까지 반복될 것입니다.)
그럼 여기서 당연히 의문이 하나 드실 것입니다.
"그래서 cost(W)의 값을 최소화시킬 수 있는 방향을 어떻게 아는데??"

자, 위의 사진에서 W의 값을 작은 공이라고 생각해 봅시다.
그러면, 공은 어느 방향으로 굴러가나요?
위의 경우, 경사가 왼쪽 아래로 져 있으므로 공은 왼쪽으로 굴러가게 될 것입니다.
그러면, 이 공은 어디까지 굴러갈까요?
cost(W) (위 이미지에선 J(w)라고 적혀있음)의 값이 가장 작아지는,
다시 말해서 가장 높이가 아래에 있는 곳까지 굴러갈 것입니다.
Gradient Descent는 이러한 원리와 동일하다고 봐도 됩니다.
W값이 처음 주어졌을 때, 우선 그 W값에 대한 경사를 먼저 구합니다.
그 후, 그 경사가 진 방향으로 W값을 바꿔줍니다.
경사가 왼쪽 방향으로 져 있다면, W값을 빼주고...
경사가 오른쪽 방향으로 져 있다면, W값을 더해주는 식으로 말이죠.
그렇게 한다면, 저 함수에서 가장 작은 cost(W)의 값을 가지는 W의 값을 구할 수 있게 됩니다.
Gradient Descent는 이렇게 단순한 생각을 갖고 만들어진 알고리즘입니다.
그런데, 그 각각의 W값에 대한 경사는 어떻게 구하냐고요?
그 경사를 구하기 위해서, 우리는 저 함수를 W값에 대하여 미분해 줄 것입니다.
(미분이 뭔지 잘 모르신다면, 간단하게 그냥 함수의 기울기를 구하는 방법 정도로 이해하시면 됩니다.)

지금부터의 내용은, 기본적으로 미분을 알고 있어야 이해가 가능합니다!
미분을 모르신다면, 그냥 저 아래로 쭉 내리시면 되겠습니다.
우선, f(x)^2를 미분하면 2 * f(x) * f'(x)가 됩니다.
그런데, 그 값에 그냥 m분의 1만 곱해버리면 상수 2가 남아버리니 계산하기 귀찮아지므로...
m분의 1 대신 2m분의 1을 곱하는 것으로 식을 바꾸겠습니다.

f(x)^2를 미분하면, 2 * f(x) * f'(x)가 된다는 사실을 이용하면,
(Wx - y)^2를 미분하면
2 * (Wx - y) * x 가 됩니다.
그리고 시그마 앞에선 2가 앞으로 넘어갈 수 있으므로,
2를 앞으로 넘기면 시그마 앞의 값은 1/2m * 2 = 1/m이 됩니다.
결국, W값은 W값에서 (Wx - y) * x의 평균을 낸 값을 뺀 값으로 업데이트해 줍니다. (위의 식 참고)
참고로, 위의 알파 값은 Learning Rate라는 것으로, 이에 대한 자세한 내용은 다른 시간에 알아봅시다.
Q. 왜 W값에서 "(Wx - y) * x의 평균을 낸 값"을 더하지 않고 빼는 것인가요?
A. 경사가 왼쪽을 향하고 있을 때, 그때의 미분 값은 양수인 가요, 음수인가요?
예, 경사가 왼쪽으로 져 있다면, 그 미분 값 (경사의 기울기 값)은 양수가 됩니다.
그런데 경사가 왼쪽으로 져 있으면, W값을 왼쪽으로 옮겨야겠죠? (즉, W값을 감소시켜야겠죠?)
그러므로, W값에서 양수를 빼주어야 W값이 감소하기 때문에, 저 값을 더하지 않고 빼는 것입니다.
반대로 경사가 오른쪽으로 져 있을 때에는 미분 값(기울기 값)이 음수가 되는데,
W값을 증가시켜 주어야 하므로,
음수를 빼주어서 W값을 증가시키는 것입니다.

그런데, 저 미분을 죄다 하고 있을 시간은 사람에게 없습니다.
그런 일 따위는 컴퓨터에게 시킬 수 있습니다.
즉, 미분 사실 몰라도 공식만 대충 집어넣으면 된다는 거죠,
(게다가 텐서 플로우를 비롯한 대부분의 머신러닝 툴에서는 Gradient Descent는 모두 지원합니다.)

그런데 만약 함수가 이따구로 생겼다면 어떻게 될까요?
어느 점에서 시작하느냐에 따라 경사가 진 곳이 죄다 다르므로, 향하는 방향이 죄다 다르게 됩니다.
결국, W값이 우리가 원하는 "함수 전체에서의 최솟값"으로 가는 것이 아니라,
"일정 구간만에서의 최솟값"으로 가게 됩니다.
이를 각각, "Global Minima"와 "Local Minima"라고 부릅니다.
아무튼, 저렇게 생긴 함수에선 그냥 W값이 Local Minima에 처박힐 가능성이 매우 높기에, Gradient Descent의 성능이 매우 떨어집니다.
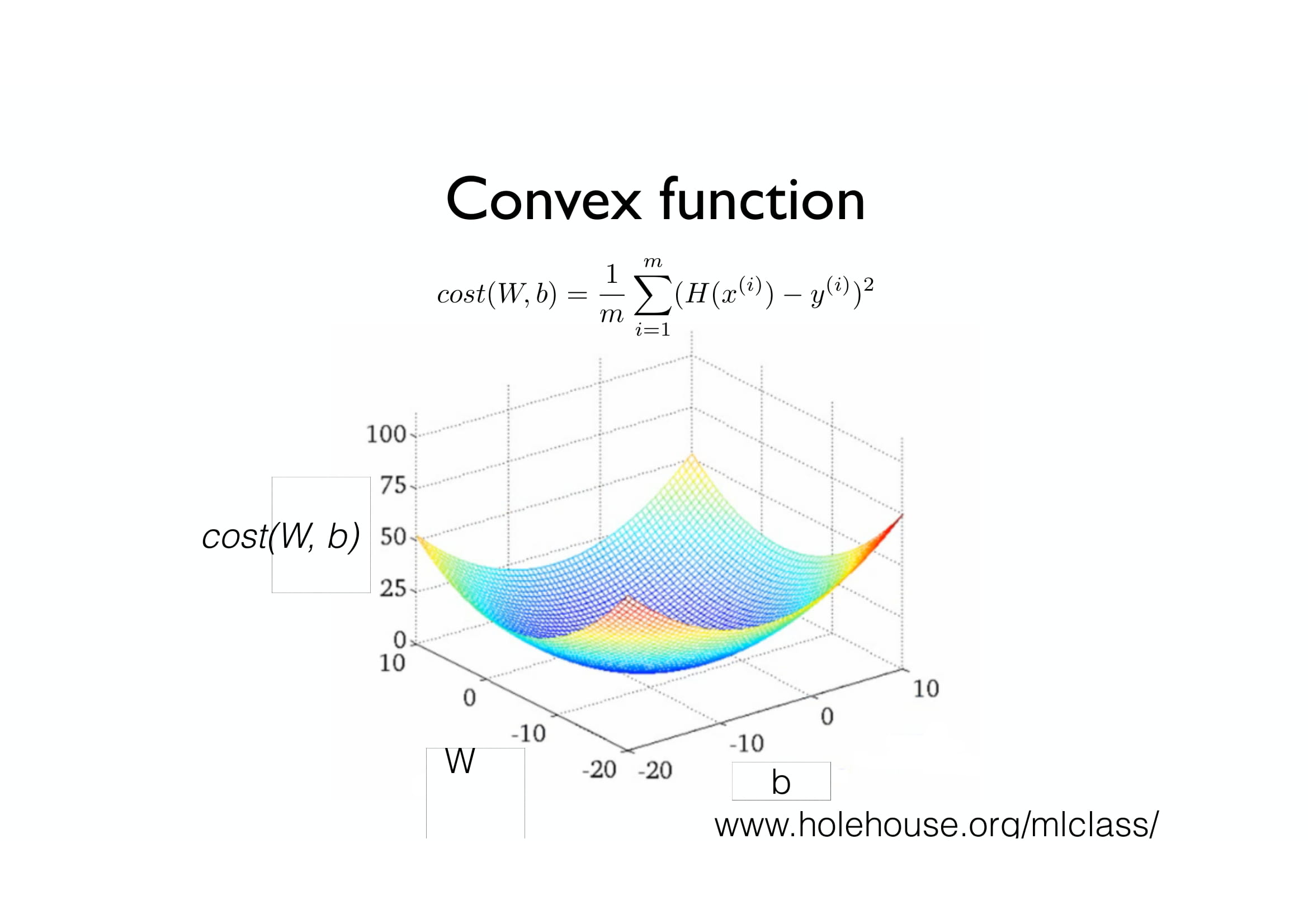
그러므로, 우리는 Cost function을 저렇게 이상하게 생긴 함수로 두면 안되고,
아름다운 밥그릇 모양 (중간이 패인 트램펄린 모양?)으로 생긴 함수를 사용하여야 합니다.
그러면, 결국 Local minima가 한 개뿐이므로 Local Minima가 Global Minima와 같은 것이 됩니다.
이런 식으로, Local minima와 Global minima가 동일한 아름다운 함수를 우리는 Convex function이라고 부릅니다.
그러므로, 우리는 Convex function을 Cost function으로 사용하여야 합니다.

다음 시간에는, Multi-variable Linear Regression(다변수 선형 회귀)에 대해 배워보겠습니다.
(왜 로지스틱이라고 적혀있는지는 잘 모르겠습니다;; 분명 다음엔 Linear regression인데;)
그럼 안녕!
'인공지능 > 모두를 위한 딥러닝 (sung kim) lec' 카테고리의 다른 글
| 모두를 위한 딥러닝 부록편 - 미분의 개념과 Gradient Descent (1) | 2019.05.10 |
|---|---|
| 모두를 위한 딥러닝 (sung kim) lec5 - Logistic Classification (로지스틱 회귀분석) (0) | 2019.05.09 |
| 모두를 위한 딥러닝 (sung kim) lec4 - Multivariable Linear Regression (다변수 선형 회귀) (1) | 2019.04.09 |
| 모두를 위한 딥러닝 (sung kim) lec2 - Linear regression & cost function (0) | 2019.03.30 |
| 모두를 위한 딥러닝 (sung kim) lec1 - 머신 러닝 기초 (0) | 2019.03.28 |
강화 학습 강의 (CS234) 1강 (1) - 강화 학습이 뭘까? / Markov란?
원래는 Deepmind의 강의 영상을 바탕으로 강화 학습 관련 글을 작성하려 했으나, 얼마 전에 스탠포드 대학교의 강의인 CS234의 영상이 유튜브에 올라온 것을 보고 그를 바탕으로 글을 작성합니다.
슬라이드 / 렉쳐노트 : http://web.stanford.edu/class/cs234/schedule.html
영상 : https://www.youtube.com/playlist?list=PLoROMvodv4rOSOPzutgyCTapiGlY2Nd8u
강의 내용을 정리하고, 영어로 된 영상을 보지 않고도 강화 학습을 배울 수 있도록 글을 작성합니다.
* 주의 - 기본적인 머신 러닝에 대한 이해도가 있어야 합니다! 제 티스토리의 "머신 러닝 기초" 를 먼저 보시거나, 다른 머신러닝 강의를 보며 머신 러닝을 학습하는 것을 추천드립니다.

오늘부터 시작할 강화 학습 강의입니다.
언제나 그렇듯, 강화 학습이 무엇인지 먼저, 간단하게 강화 학습이 무엇인지 먼저 알아가 보도록 합시다.

강화 학습을 한 줄로 요약하자면,
"순차적 선택을 잘 하도록 학습하는 것" 이라고 합니다.
이 한 문장 속에 앞으로 해나가야 할 굉장히 많은 내용들을 함축하고 있는데, 한번 쪼개 보도록 하겠습니다.
우선, 인공지능에게 "순차적 선택"을 할 수 있도록 해야 합니다.
즉, Yes or No 로 이루어진 단순한 선택이 아닌, 게임을 플레이하듯, 운전을 하듯 순차적인 일련의 선택들을 잘해나가도록 해야 한다는 것이죠.
그리고, 그러한 선택을 "잘" 하도록 해야 합니다. 그러기 위해서는 무엇이 "좋은" 선택인지 알아야 하고, 상황에 따른 최적의 선택을 찾아내야 하죠.
마지막으로, "학습"을 해야 합니다. 그리고 이것이 바로 강화 학습 (사실 머신러닝 대부분)의 가장 중요한 부분이죠.
사실 AI의 가장 중요한 점은 이미 경험하지 않은, 즉 "확실하지 않은" 상황 속에서도 좋은 선택을 하게 만드는 것이죠.
특히 강화 학습에서는, 이전 경험에 빗대어 그 상황을 직접 경험하지 않고도 최적의 결과를 내는 방식으로 학습합니다.
(더 자세히는 나중에 설명합니다!)

일단 강화 학습의 예시를 보도록 합시다.
사실 CS234 강의에는 좀 다양한 예시가 나오긴 하는데, 그거 다 설명하기는 좀 그렇고 가장 대표적으로, 그리고 보통 가장 처음 해보게 되는 게임 강화 학습에 대한 예시를 보도록 하겠습니다.
https://www.youtube.com/watch?v=V1eYniJ0Rnk
위의 퐁같은 경우가 바로 강화 학습이 적용된 예시입니다.
순차적 선택 (밑의 바를 움직이는 것) 을,
잘 (최대한 점수가 높게),
학습 (컴퓨터가 플레이함)
시키는 것이죠.

강화 학습에서 중요하게 다루는 측면은 크게 네 가지로 분류할 수 있습니다.
바로, Optimization, Delayed consequences, Exploration, Generalization 입니다.
Optimization이란, 다양한 상황 속에서 할 수 있는 다양한 결정 중에서 가장 최적의 (또는 그냥 좋은) 결정을 하도록 만드는 것입니다. Optimization은 강화 학습 뿐만 아니라, 다른 머신러닝 기술에서도 다루는 내용입니다.
Delayed consequences는 지금 한 선택이 한참 나중에도 좋은 선택인지 아닌지 잘 모른다는 것입니다.
가령, 지금 당장 아이스크림을 5개를 동시에 먹어도 한 시간 정도는 배가 아프지 않지만, 한 시간 후에 갑자기 배가 아파올 수도 있겠죠? 이렇듯, 지금 한 일이 나중에도 영향을 미치는 것을 말합니다. 일반적인 머신 러닝에서는 볼 수 없는, 강화 학습만의 주요한 특징 중 하나입니다.
Exploration은 말 그대로, 탐험하는 것입니다. 많은 결정들을 하면서 세상에 대해 배우는 것이죠.
여기서 가장 큰 문제점은, 바로 우리는 우리가 이미 한번 해봤던 것에 대해서만 안다는 것이죠.
공부도 조금 해 봐야지 내가 얼마나 공부에 적성이 있는지 알게 되고, 게임도 조금 해 봐야지 재미있다는 것을 알게 되는 것과 마찬가지입니다.

마지막으로, Generalization입니다. 직역하자면, 일반화죠.
아까 전에 했던 퐁의 예시로 돌아가 봅시다. 사실 이 AI는 따로 게임의 룰을 알려주어 학습시킨 것이 아니라 단순한 픽셀 값들만으로 게임을 플레이하도록 학습시킵니다.
그런데, 만약 이런 AI를 수작업으로 만든다면 어떻게 될까요? 각 픽셀을 하나의 경우의 수로 놓는다면, 수없이 많은 경우의 수에 대한 선택들을 제시해야만 합니다. 사실상 말이 안 되는, 어마 무시한 값이죠.
그렇기 때문에, 이러한 것들을 단순한 픽셀로 볼 것이 아니라, 다른 방식으로 일반화시켜야 합니다. 데이터(픽셀 값)들로만 학습하는 것보다 훨씬 더 나은 성능을 제공할 뿐만 아니라, 더욱 고수준으로 해야 할 작업을 나타낼 수 있기 때문이죠.
이 네 가지 중에서, 가장 "강화 학습만의 특징"이라고 할 수 있는 것은 바로 "Exploration"입니다. AI Planning, Supervised Learning, Unsupervised Learning, Imitation learning 등 다양한 기술들은 모두 Optimization과 Generalization이 중요하고, 그중 AI Planning과 Imitation Learning에서는 Delayed Consequences 를 고려하기도 하지만, Exploration은 하지 않습니다. Exploration이 그만큼이나 독특한 특징이라는 것이죠.
... 여기까지가 15분짜리 내용입니다.. 줄일 거 줄인다고 썼는데도 기네요;;
계속한번 가봅시다!!

이제 한번 조금 더 자세히 들어가 봅시다.
들어가기에 앞서, 기본 용어들을 대충 정리하자면...
Agent : 우리가 학습시키고자 하는 AI.
Action : 행동.
Observation : 관찰. Agent가 보고 듣는 것.
Reward : 보상. 어떤 Action을 취했을 때 얻는 점수의 개념임.
World : 세상. 일반적으로 학습시키고자 하는 환경을 의미함. (게임의 경우 게임 세상)
(단어장 아님 주의)
그래서 강화 학습의 궁극적 목표는,
"Agent가 World에 대한 Observation을 통해, 최적의 Reward를 얻는 Action을 찾는 것" 입니다.
이를 위해선 즉각적인 보상과 먼 나중에 있을 잠재적인 보상의 균형을 맞춰줘야 할 수도 있고, (Delayed Consequence)
높은 reward를 얻기 위한 행동 전략을 필요로 할 수도 있습니다.
물론, 이것들이 필수인 것은 아닙니다. 문제 상황의 경우에 따라 필요할 수도, 필요하지 않을 수도 있습니다.

웹 광고의 경우, Agent는 웹에 띄울 광고를 띄워주고, 그때 시청 시간과 광고 클릭률 등을 보고(Observation) 학습합니다.
이 경우엔 즉각적 보상과 잠재적 보상의 균형을 맞출 필요도 없고,
특정한 전략을 요구하지도 않습니다.

혈압 조절 같은 경우, Agent가 환자에게 운동을 시키거나 약을 투여하는 행동 중 하나를 권유할 수 있습니다.
그리고, 만약 그 권유를 들은 환자가 건강해지면 +1의 보상을 얻고, 약 투여의 부작 용당 -0.05의 보상을 얻습니다. (잃는 거죠 ㅎㅎ)
운동을 바로 시작한다면 바로 건강해지진 못하겠지만, 추후에 건강한 범위 안에 들어올 수는 있겠죠.
이를 통해, 즉각적 보상과 잠재적 보상 사이의 균형을 맞춰야 할 필요가 있을 것입니다.
약을 투여한다면 즉각적으로 환자가 건강해질 수는 있겠지만, 추후 부작용이 있을 수도 있겠죠.
즉, 약을 투여하는 것에는 특정한 행동 전략이 필요하다는 것이죠.

이제 이것들을 조금 수식화(?) 시켜봅시다.
시간은 원래는 연속적이지만, 그 연속적인 시간 하나하나를 쪼갤 수는 없으니 시간을 불연속적으로 설정하고... (가령, 게임의 경우 프레임 단위)
지금까지의 내용을 대충 정리해 본다면,
각각의 time step t 에 대하여,
Agent 는 Action at 를 취하고,
World 는 at 에 대한 Observation인 ot 와 Reward인 rt 를 내며,
다시 Agent는 그 ot 와 rt 를 갖고 학습합니다.
(작은 영어 어떻게 치나요 ㅠㅠㅠ)
..라고 할 수 있겠죠?

그런데, 이런 a, o, r들을 어디다 써먹을까요?
우리가 Agent를 학습시킬 때, 어떤 방식으로 Agent를 학습시킨다고 했었죠?
과거의 경험을 바탕으로, 추후에 어떤 행동을 취할지 결정한다고 했었습니다.
그렇다면, a1, o1, r1,... at, ot, rt 들을 모아서 이것들을 바탕으로 다음 결정을 취한다고 할 수 있겠지요?
(t는 현재 time step을 의미합니다.)
이렇게 결정을 내릴 때 사용하는 정보를, State라고 합니다.
그리고, 이런 State는 결국 History를 바탕으로 나오는 것이므로,
각각의 State는 일종의 History의 함수이다. ( St = f(Ht) )
라고 할 수 있습니다.
여기서 함수라고 하면, 일차함수, 이차함수와 같은 개념보다도 일종의 프로그래밍에서의 함수로 보는 것이 더 적절해 보입니다. 즉, 일정 데이터 값들에 대해 특정 행동을 취하게 만드는 것입니다.

World State란, 실제로 세상이 어떻게 돌아가는지를 알려주는 정보를 의미합니다. 어떤 행동을 했을 때 어떻게 관측되고, 어떤 보상이 주어지는지를 의미하는 것이죠.
가령, 위의 게임인 퐁의 경우, 공이 블럭에 맞으면 블럭이 부서진다거나 블럭을 부수면 보상이 들어온다거나 하는 등의Observation과 Reward가 주어집니다.
하지만, 대부분 Agent에게는 이러한 정보가 주어지지 않습니다. 아까 Pong의 예시를 들 때, Pong의 Agent는 픽셀 값으로만 학습한다고 했었죠? 즉, 이 Agent는 "블럭을 부수면 점수가 들어온다" 라는 정보는 주어지지 않았었다는 것이죠.
그리고 어떠한 사실을 안다고 하더라도, Agent에게 별 쓸데없는 내용일 수도 있습니다. 가령, "Pong에서는 블럭들이 층별로 색이 다르다." 와 같은 것도 World State라고 할 수 있는데, 사실 이러한 내용은 Agent에게는 전혀 쓸데없는 내용인 것과 같은 것입니다.
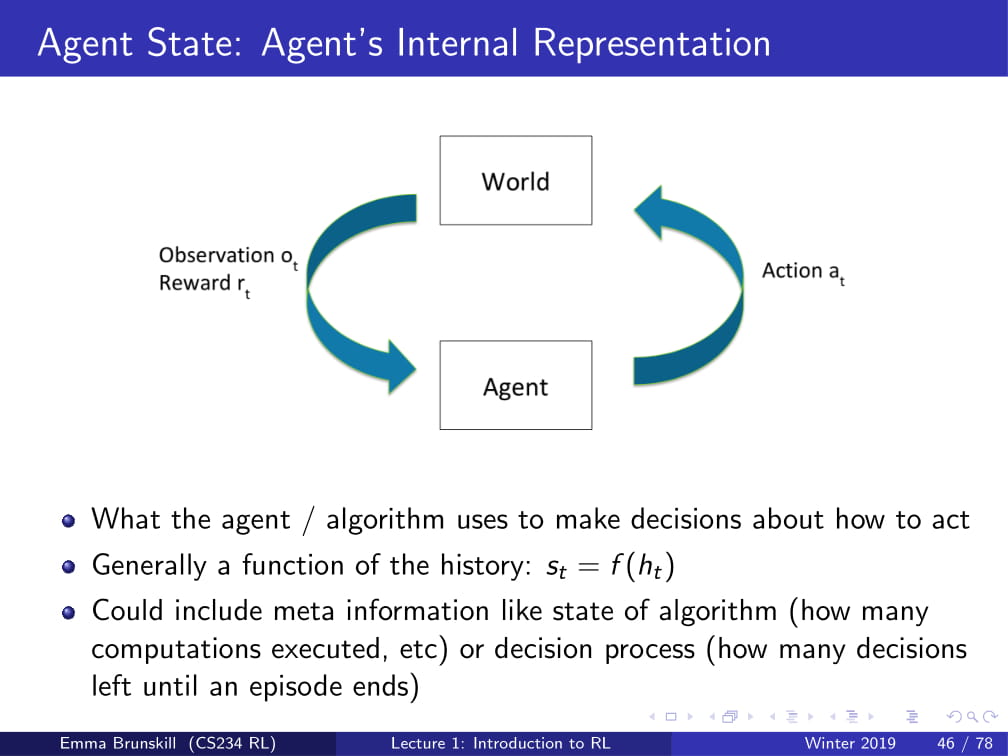
그 반면, Agent State는 Agent가 특정 선택을 할 때 사용할 수 있는 정보입니다.
이러한 World State와 Agent State의 관계는, 인간의 시야로 예를 들 수도 있습니다.
우리 시야는 약 180도가량을 볼 수 있습니다. 이때, 이 우리의 시야 안에 들어오는 것들이 바로 Agent State입니다.
하지만, 세상은 우리가 보는 이 180도만 있는 것이 아니라, 내 뒤나 위나 아래에도 세상이 있습니다. 우리의 시야 안에 들어와 있지는 않지만, 확실히 존재하는 세상입니다. 이것이 바로 World State입니다.
아무튼, 다시 Agent State 이야기로 돌아오겠습니다. 아까 전에 State는 History의 함수라고 할 수 있다고 했었죠?
이때의 State는 보통 Agent State를 의미합니다. (World State는 어차피 Agent가 모르는 정보라서 크게 의미가 없습니다.)

이번엔 Markov Assumption에 대해 알아봅시다.
Markov Assumption이란, 충분한 정보가 담긴 State가 존재할 때,
이 State만으로 예측한 미래가 History로 예측한 미래와 같을 때, 이를 Markov 한 State라고 합니다.
즉, 현재의 State 하나만 주어지더라도, 지금까지의 모든 History와는 관계없이 미래를 예측할 수 있다고 하는 것입니다.
다시 말해, 미래를 예측하는 데는 과거에 대한 정보가 필요 없고, 그냥 그런 정보들을 잘 모아놓은 현재의 상황, State만이 필요하다는 것입니다.

그렇다면, 한번 예시를 들어 설명해 보겠습니다.
첫 번째로, 고혈압 조절을 예시로 들어보겠습니다.
State를 현재 혈압 수치라고 하고, 약을 투여할지 하지 않을지를 결정하는 것은 Markov 하다고 할 수 있을까요?
그렇지 않을 것입니다. 왜냐하면, State는 현재 혈압 수치만을 알려주기 때문에, 내가 지금 운동을 해서 혈압이 높아진 것일 수도 있고, 공포영화를 봐서 혈압이 높아진 것일 수도 있는데 현재의 혈압만을 보고 약을 투여할지 여부를 결정하는 것은 옳지 못하기 때문입니다.
두 번째로, 웹사이트 쇼핑 인공지능입니다.
State를 현재 구매자가 보고 있는 상품이라 하고, 그 구매자에게 어떤 다른 상품을 추천할지를 결정하는 것은 Markov 하다고 할 수 있을까요?
이것도 마찬가지로, Markov가 아닙니다. 지금 보고 있는 상품이 그냥 심심해서 랜덤으로 들어온 상품일 수도 있고, 광고를 잘못 눌러서 들어온 상품 페이지일 수도 있는데 그 사용자에게 다른 상품을 무작정 추천하는 것을 좋지 못한 행동이기 때문입니다.

그런데 왜 Markov Assumption을 사용할까요?
왜냐하면, 일반적으로 State를 잘 설정한다면, 언제나 Markov 하다고 말할 수 있기 때문입니다.
가령, State를 그냥 History 전체라고 한다면, 그 State는 언제나 Markov 하다고 할 수 있습니다. (결국 st = ht이므로..)
그리고, 실제로 대부분 최근의 Observation들만으로도 충분한 정보가 담긴 State가 됩니다.
즉, 가장 최근의 Observation만으로 이루어진 State도 Markov하다고 할 수 있는 경우가 많은 것이죠.
그리고, State는 사실 정확하면서도 작은 것이 좋습니다.
State가 커버리면, 연산하기에도 너무 어렵고, 데이터를 가져오는 것도 힘들며, 결과를 내는 성능에 영향을 끼칠 수도 있기 때문입니다.
가령, 우리 인생의 State가 우리 인생 History 전부라고 했을 때,
그 State를 어떻게 연산하는 것은 손도 못 댈 일이 될 것이며,
그 History의 데이터를 수집하는 것도 어려운 일이 될 것입니다.
또한, 모든 History를 그냥 State에 넣어버리면, 모든 각각의 State는 다른 것이 되므로, (가령, 팔을 들어 올리는 행위 하나만 봐도 최소한 몇 mm 정도는 차이가 날 것이므로...) 그것들만으로 미래를 예측하는 것이 힘들어져 결국 성능이 저하되는 결과를 불러오는 것입니다.
이러한 단점들은 사실 Deep Reinforcement Learning에 들어와서는 서서히 사라지고 있긴 하지만, 아무튼 우리가 지금 배울 내용들에 대해서는 굉장히 중요한 사안입니다.
.....까지가 40분 내용입니다;;
이렇게 쓰다간 한도 끝도 없이 길어질 것이 뻔하므로, 여기서 대충 마치도록 하고,
다음 시간부터 MDP에 대해 알아보도록 합시다!
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
|---|---|
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |