분류 전체보기
-
[백준] 24916 - 용암 점프 힌트, 풀이 및 코드(C++)2022.06.29
-
[백준] 1800 - 인터넷 설치 힌트, 풀이 및 코드 (C++)2022.06.29
-
[백준] 22988 - 재활용 캠페인 힌트, 풀이 및 코드(C++)2022.03.27
-
딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃2020.07.29
[백준] 24916 - 용암 점프 힌트, 풀이 및 코드(C++)
https://www.acmicpc.net/problem/24916
24916번: 용암 점프
경기과학고등학교 학습실에는 때때로 용암이 찬다. 이 용암 바닥에 왼쪽에서 오른쪽으로 1부터 N까지의 정수 번호가 매겨진 N 개의 발판이 떠 있다. i의 번호가 매겨진 발판의 위치는 하나의 정
www.acmicpc.net
1. 문제
- x축 위에 점들이 N개($n \leq 100,000$) 있음
- 초기에 i번째 점에서 시작해서, 모든 N개의 점을 순회할 수 있는지 확인해야 함
- 단, 이동 시에는 이전에 이동했던 거리의 최소 2배 이상 이동해야 함
- 각 N개의 점에 대해서, 각 점에서 출발하여 모든 N개의 점을 순회할 수 있으면 YES를, 없으면 NO를 출력함.
1-1. 힌트
힌트 1
모든 테스트케이스에서의 N의 범위가 $N \leq 1,000,000$이므로, 각 N개의 점에 대해서 200번 이하의 연산을 진행해야 시간 초과가 나지 않는다.
힌트 2
초기의 이동 거리가 단 1이라고 하더라도, $2^{21}=2,097,152$이기 때문에 20번만 이동하더라도 이미 x축의 범위인 $10^{-6} \leq a_i \leq 10^6$에 의해 더 이상 다음 점으로의 이동이 불가능하다.
힌트 3
한 점에서 다른 점으로 이동할 때, 어떤 한 점을 건너뛰고 이동하는 경우 어떻게 되는가?
(즉, A<B<C인 세 점에서 A->C로 이동하는 경우)
2. 문제 관찰 과정
우선, 문제의 조건과 시간 제한을 살펴보자.
모든 테스트케이스에서의 N의 범위가 $N \leq 1,000,000$이므로, 각 $N$개의 점에 대해서 200번 이하의 연산을 진행해야 시간 초과가 나지 않는다(대략 1억회의 연산을 1초라 가정함). 하지만 정답을 YES로 출력하는 점에 대해서는 필연적으로 해당 점에서부터 모든 $N$개의 점을 순회해야 하므로 시간복잡도가 $O(N^2)$이 된다. 즉, 문제에 숨겨진 또 다른 조건을 찾아야 한다는 뜻이다.
문제에서 이동 거리는 최소 1이고, 다음에 이동할 때는 이전 거리의 2배는 이동해야 한다고 제시하였다. 그런데, $2^{21}=2,097,152$이기 때문에 초기에 아무리 조금 움직였더라도 추가로 20번만 이동하더라도 이미 x축의 범위인 $10^{-6} \leq a_i \leq 10^6$에 의해 더 이상 다음 점으로의 이동이 불가능하다. 즉, 어차피 각 테스트케이스에서 이동 횟수가 20보다 크다면 정답은 무조건 NO가 된다. 이 경우, 움직인 횟수를 $M$이라 하면 시간복잡도가 테스트케이스 당 $O(M^2)$이 되어도 $T{M}^2 = 22,050,000$이므로 시간 안에 풀이가 가능하다.
그러나 $N$개의 점에 대하여, $i$번째 이동에 $N-i$개의 점으로 이동이 가능하므로 완전 탐색 시뮬레이션을 돌리게 되면 시간 복잡도가 $N!$이 되어 시간 안에 풀이가 불가능하다. 어떻게 $O(N!)$의 시간복잡도를 $O(N^2)$으로 바꿀 수 있을까?
3. 풀이
위 문제 풀이의 가장 중요한 아이디어는 다른 점을 건너뛰고 이동하면 안 된다는 것이다.
예를 들어, $A < B < C $인 세 점에서 $A$에서 $C$로 이동한 경우를 생각해 보자.
점 $A$와 점$C$ 사이의 거리가 $x$라고 두면, 다음으로 이동할 수 있는 거리는 최소 $2x$이다.
이 때, 점 $C$에서 오른쪽으로 $y (2x \leq y)$만큼 이동하면 그 다음으로 이동할 수 있는 위치는 $C+2y$ 이상, $C-2y$이하이므로 결코 점 $B$에 도달할 수 없다.
마찬가지로 점$C$에서 왼쪽으로 $y$만큼 이동하는 경우에서도 결코 점 $B$로 도달할 수 없다.
이렇듯, 다른 점을 건너뛰고 이동하면 필연적으로 그 사이에 있는 점으로는 도달할 수 없다는 점을 확인할 수 있다.
하지만 이 사실을 알아내더라도 좌/우로 모두 이동하는 것을 완전 탐색으로 시뮬레이션을 돌리게 되면 시간복잡도는 여전히 $O(2^N)$으로, 제한 시간 내에 풀이가 불가능하다.
좌/우 중 어느 것을 고르는 것이 최적일지 판단은 어떻게 할 수 있을까?
문제를 간단히 하기 위해, $A < B < C$ 인 세 점 중 점 $B$ 에서 시작하는 경우를 예시로 들어 보자.
$A$와 $B$ 사이의 거리를 $x$, $B$와 $C$ 사이의 거리를 $y$라고 하자.
점$B$에서 점$A$로 이동하는 경우 다음으로 이동할 수 있는 위치는 $A+2x$ 이상 $A-2x$ 이하이다.
이 때, $y<x$인 경우 $A-2x < C < A+2x$이므로 절대로 점$C$로 이동할 수 없다.
즉, 좌/우 중 한 곳을 선택하는 경우, 무조건 짧은 거리만을 선택해야 한다는 것이다.
위 아이디어들을 종합하면, 다음과 같은 풀이가 도출된다.
"$N$개의 점에 대해, 항상 좌/우 중에서 가장 가까운 거리에 있는 점으로 이동한다(이 때, 좌/우의 거리가 동일한 경우에는 좌/우 모두 이동해 본다). 그렇게 이동하면서 다음에 이동할 점이 결코 도달 불가능한 점에 있을 경우 답은 NO이고, 끝까지 $N$번째 점으로 이동했다면 답은 YES이다."
이것을 코드로 그대로 구현해 보자.
4. 코드
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int n;
vector<ll> a;
bool solve(int x, int r, int l, ll gap) {
if (l>=0 && r<n) {
if (a[r]-a[x]<a[x]-a[l]) {
if (gap>a[r]-a[x]) return false;
return solve(r, r+1, l, (a[r]-a[x])*2);
}
else if (a[r]-a[x]>a[x]-a[l]){
if (gap>a[x]-a[l]) return false;
return solve(l, r, l-1, (a[x]-a[l])*2);
}
else {
return (solve(l, r, l-1, (a[x]-a[l])*2) || solve(r, r+1, l, (a[r]-a[x])*2));
}
}
else if (l>=0) {
if (gap>a[x]-a[l]) return false;
return solve(l, r, l-1, (a[x]-a[l])*2);
}
else if (r<n) {
if (gap>a[r]-a[x]) return false;
return solve(r, r+1, l, (a[r]-a[x])*2);
}
else {
return true;
}
}
int main()
{
int t;
int r, l;
ll gap;
cin >> t;
while (t--) {
int x=0;
scanf("%d",&n);
a = vector<ll>(n, 0);
for (int i=0; i<n; i++) {
scanf("%lld",&a[i]);
}
for (int i=0; i<n; i++) {
gap=1234567890;
r=i+1;
l=i-1;
if (l>=0) gap = min(gap, a[i]-a[l]);
if (r<n) gap = min(gap, a[r]-a[i]);
if (solve(i, r, l, gap)) printf("YES\n");
else printf("NO\n");
}
}
}
5. 여담
위 풀이에서 최악의 케이스는 좌우가 동일한게 계속 반복되서 나오는 경우인데, 제한 조건 안에서 아무리 좌우가 동일하게 반복되어봤자 그렇게까지 많은 케이스를 방문하지 않게 되므로, 시간 내에 충분히 풀이가 가능하다.
난이도 기여를 보니까 의도된 풀이는 DP인 것 같은데, 나중에 그 풀이도 살펴봐야겠다.
'PS > 백준 풀이' 카테고리의 다른 글
| [백준] 3307 - 대회가 끝나고 난 뒤에 빰빠빰 힌트, 풀이 및 코드(C++) (0) | 2022.07.03 |
|---|---|
| [템플릿] 백준 문제 힌트, 풀이 및 코드 템플릿 (0) | 2022.07.03 |
| [백준] 15824 - 너 봄에는 캡사이신이 맛있단다 힌트, 풀이 및 코드(C++) (0) | 2022.06.30 |
| [백준] 1800 - 인터넷 설치 힌트, 풀이 및 코드 (C++) (0) | 2022.06.29 |
| [백준] 22988 - 재활용 캠페인 힌트, 풀이 및 코드(C++) (0) | 2022.03.27 |
[백준] 1800 - 인터넷 설치 힌트, 풀이 및 코드 (C++)
https://www.acmicpc.net/problem/1800
1800번: 인터넷 설치
첫 번째 줄에 N(1 ≤ N ≤ 1,000), 케이블선의 개수 P(1 ≤ P ≤ 10,000), 공짜로 제공하는 케이블선의 개수 K(0 ≤ K < N)이 주어진다. 다음 P개의 줄에는 케이블이 연결하는 두 컴퓨터 번호와 그 가격이 차
www.acmicpc.net
1. 문제
- 컴퓨터의 개수 $N$, 케이블선의 개수 $P$, 공짜로 제공하는 케이블선의 개수 $K$가 주어진다.
- 다음 $P$개의 줄에, 연결된 컴퓨터 쌍 A, B와 연결 비용 C가 주어진다.
- 초기에는 1번 컴퓨터에만 인터넷이 연결되어 있고, $N$번 컴퓨터에 인터넷을 연결하는 것이 목표이다. (1, $N$을 제외한 다른 컴퓨터는 인터넷에 연결되지 않아도 된다.)
- 연결하는 비용은 연결한 케이블선을 나열했을 때, $K+1$번째로 비용이 높은 케이블선의 비용이다.
2. 힌트
힌트 1
K=0인 경우엔 어떻게 연결하는 것이 최적일지 생각해 보자.
다른 그래프 문제와는 다르게 비용의 총 합이 아니라 사용한 비용 중 최대값이 무엇인지가 중요하다는 점에 주목하자.
힌트 2
$K=0$일때보다 $K>0$일때의 최소 비용이 당연히 더 작다.
다시 말해, $K=0$일때 선택했던 케이블선의 비용보다 더 높은 비용의 케이블선은 무료가 아닌 이상 고를 이유가 전혀 없다.
힌트 3
비용이 $X$ 이하인 간선만으로 $1$번 컴퓨터부터 $N$번 컴퓨터까지 연결하면, 몇 개를 연결하는지와 관계 없이 총 비용은 $X$ 이하일 것이다.
3. 문제 관찰 과정 및 풀이
우선, 가장 간단한 $K=0$인 경우부터 생각해 보자.
$K=0$인 경우, 무료로 주는 케이블선이 없으므로 모든 케이블선을 직접 연결해야 한다.
이 경우에는 케이블선을 최적으로 고르는 방법은 비용이 가장 낮은 케이블선부터 하나씩 차례로 연결해 보면서, $1$번 컴퓨터와 $N$번 컴퓨터가 연결될때 까지, 그리디하게 계속 연결해 보는 것이다.
그러나, $K>0$인 경우를 생각해 보자.
가장 간단하게 생각할 수 있는 방법은 $P$개의 간선 중 $K$개를 모두 고른 다음에, 위에서 말했던 해결 방법을 그대로 적용하는 것이다.
실제로 $K=1$인 경우에는 이런 방법이 통할 수 있겠지만, $K < N \leq 1,000$이고, $P \leq 10,000$이므로 $K, P$가 커지면 이 방법은 시간초과가 나게 될 것이다.
$P$개의 케이블선 중 무료로 받을 $K$개를 모두 탐색하며 문제를 푸는 것은 어떻게 해도 불가능하다는 사실을 알았으니, 여기서 몇 가지 고민들을 할 수 있다.
우선, $P$개의 케이블선 중 $K$개를 고르는 것을 그리디하게 구할 수 있는지 고민해 보면, 어떻게 해도 불가능하다는 것을 깨달을 수 있다.
가장 비싼 $K$개의 케이블선을 고르는 경우는 당연히 최선이 아닐 뿐더러, $K$개의 케이블선을 골랐을 때와 고르지 않았을 때 최소 비용의 경로가 아예 달라지기 때문이다. 즉, 무료로 받은 $K$개를 제외한 간선을 연결하기 전에는 $K$개의 무료 간선을 고를 수 없다는 것이다.
여기서 잠깐 종합해 보자.
$K=0$이라고 생각했을 때는 그리디하게 케이블선들을 연결할 수 있었다.
그렇다면 $K>0$인 경우는 어떨까?
이미 그리디하게 연결된 케이블선들 중 가장 높은 비용의 케이블선 $K$개를 무료로 받을 때, 무료로 받은 케이블선 비용 미만의 케이블선과, 지금 무료로 받은 케이블선들만으로 $1$번 컴퓨터와 $N$번 컴퓨터를 연결할 수 있다면 최소 비용은 조금씩 낮아지게 된다.
이 때, 만약 처음에 $X$ 이하의 비용만으로 이미 $1$번 컴퓨터와 $N$번 컴퓨터를 연결할 수 있었다고 한다면, 무료로 받는 케이블선이 아닌 이상 $X+1$ 이상의 비용을 가진 케이블선을 추가로 고를 필요가 전혀 없다.
또한, 비용이 $X$ 이하인 케이블선만 고른다면 고른 케이블선이 $1$번 컴퓨터와 $N$번 컴퓨터를 연결하는지 여부와 관계 없이 어차피 총 비용은 $X$ 이하이다.
따라서, 우리는 이런 풀이를 생각해볼 수 있다.
"비용이 $X$ 이하인 케이블선들을 모두 고른 뒤에, $K$개 이하의 케이블선만으로 $1$번 컴퓨터와 $N$번 컴퓨터까지 연결할 수 있다면, 총 비용은 $X$ 이하일 것이다."
여기까지 왔다면 풀이 방식이 상당히 다양한데, 필자는 다익스트라 기법으로 접근했다.
케이블 쌍 개수가 $10,000$개 이하이므로 사실 케이블선 비용의 종류는 최대 $10,000$개이다.
그래서, $solve(x)$를 "비용이 $x$ 이하인 간선을 제외하고 $K$개 이하의 간선만을 이용하여 $1$번 컴퓨터와 $N$번 컴퓨터를 연결할 수 있는가?" 라는 뜻으로 만들었다.
그리고 나서, $1$번 노드부터 시작해서 비용이 $x$ 이하라면 $cost$값을 그대로 두면서 pq에 집어넣고, $x$ 초과라면 $cost$값을 1 증가시키면서 pq에 집어넣었다.
그렇게 맞았습니다!! 를 받을 수 있었다.
그런데.. 사실 이 풀이는 간단히 생각하면 $O(P^2 log(N))$이라 시간 안에 안될 가능성이 있다.
물론 저런 시간복잡도가 나오려면 정말 최악의 경우로 나와야 하지만, 가격이 $1,000,000$ 이하이고 케이블선 개수도 $10,000$개 이하이므로 사실 이론적인 최악의 경우로 나오는 것이 불가능하므로 문제가 풀린다.
다만 조금만 더 생각해 보면 더 빠른 풀이를 생각할 수 있는데, 매개변수 탐색(Parametric Search)를 사용하면 더욱 빠르게 문제를 풀 수 있다.
즉, 어차피 비용은 $1,000,000$ 이하이므로 l=$0$, r=$1,000,000$으로 두고 이분 탐색을 진행하며 $solve(mid)$가 $True$값을 내는 최소 $mid$값이 정답이라고 하고 제출하는 것이다.
이러면 시간복잡도는 $O(P log(N) log(1,000,000) )$이 되므로, 무조건 시간 안에 풀린다.
아래 코드는 매개변수 탐색 방법을 적용하여 푼 코드이다.
4. 코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
vector<vector<pair<int, int>>> v;
int n, p, k;
bool solve(int piv) {
// piv 이하의 간선을 제외한 k개의 간선만 사용해서 1~n링크를 만들 수 있는지 여부 판단
vector<int> cost(n+1, n);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, 1});
while (!pq.empty()) {
int node = pq.top().second;
int maxx = pq.top().first;
pq.pop();
if (cost[node] <= maxx) continue;
cost[node] = maxx;
for (int i=0; i<v[node].size(); i++) {
if (v[node][i].second <= piv && cost[v[node][i].first] > maxx) {
pq.push({maxx, v[node][i].first});
}
else if (v[node][i].second > piv && cost[v[node][i].first] > maxx + 1) {
pq.push({maxx+1, v[node][i].first});
}
}
}
if (cost[n]<=k) return true;
else return false;
}
int main() {
int ans;
int a, b, c;
int costs[1000001];
memset(costs, 0, sizeof(costs));
cin >> n >> p >> k;
v = vector<vector<pair<int, int>>>(n+1);
for (int i=0; i<p; i++) {
cin >> a >> b >> c;
v[a].push_back({b, c});
v[b].push_back({a, c});
costs[c]=1;
}
costs[0] = 1;
ans = -1;
int l, r, mid;
l=0; r=1000001; mid=(l+r)/2;
while (l<r) {
mid = (l+r)/2;
if (solve(mid)) {
ans = mid;
r = mid;
}
else {
l = mid + 1;
}
}
cout << ans;
}
5. 여담
사실 풀기 전에 "매개 변수 탐색 각인데?" 했다가 "안해도 풀리겠다" 싶어서 그냥 풀었는데, 풀고 나서 태그에 매개 변수 탐색이 박혀 있길래 매개변수 탐색으로 다시 한번 풀어봤다.
문제 출제 년도가 2008년이다보니까 $P$ 조건을 굉장히 널널하게 준 것 같은데, 아마 최근 대회였으면 $P$ 조건을 10만정도로 주지 않았을까 싶다.
'PS > 백준 풀이' 카테고리의 다른 글
| [백준] 3307 - 대회가 끝나고 난 뒤에 빰빠빰 힌트, 풀이 및 코드(C++) (0) | 2022.07.03 |
|---|---|
| [템플릿] 백준 문제 힌트, 풀이 및 코드 템플릿 (0) | 2022.07.03 |
| [백준] 15824 - 너 봄에는 캡사이신이 맛있단다 힌트, 풀이 및 코드(C++) (0) | 2022.06.30 |
| [백준] 24916 - 용암 점프 힌트, 풀이 및 코드(C++) (0) | 2022.06.29 |
| [백준] 22988 - 재활용 캠페인 힌트, 풀이 및 코드(C++) (0) | 2022.03.27 |
[백준] 22988 - 재활용 캠페인 힌트, 풀이 및 코드(C++)
https://www.acmicpc.net/problem/22988
22988번: 재활용 캠페인
첫 번째 용기와 두 번째 용기를 가져가서 용량이 $\left(0+1+\frac{13}{2}\right)$㎖ $=$ $7.5$㎖ 남은 용기를, 세 번째 용기와 네 번째 용기를 가져가서 용량이 $\left(2+3+\frac{13}{2}\right)$㎖ $=$ $11.5$㎖ 남은 용
www.acmicpc.net
1. 문제
- 초기에 통 개수 $N$과 통의 용량 $X$가 주어짐.
- 다음 줄에, $i$번째 용기에 담겨 있는 헤어에센스의 양 $C_i$가 $N$개 공백으로 나누어 주어짐.
- 통 $A, B$두개를 가져가면 $min(A+B+{X \over 2}, X)$만큼이 차 있는 통으로 바꿔줌.
- 용량이 꽉 찬 통을 최대 몇 개 만들 수 있는지 구해야 함.
2. 힌트
힌트 1
통 하나를 꽉 채우기 위해 필요한 남은 통의 최대 개수는 몇 개일까?
힌트 2
남은 통 두 개로 꽉 찬 통을 만들기 위해 필요한 조건은 무엇일까?
힌트 3
남은 통 두 개로 꽉 찬 통 하나를 만들 때, 최적으로 매칭하는 방법은 어떤 것이 있을까?
3. 문제 관찰 과정 및 풀이
통의 개수 $N \leq 100,000$ 이므로 시간복잡도 $O(N^2)$으로는 풀이가 불가능하다는 것을 알 수 있다.
또한, 통의 용량 $X \leq 10^{18}$이므로 크기 제한에 유의하여 long long 자료형을 사용해야 한다.
당연히도, 이미 남아 있는 통 중 꽉 찬 통이 있다면 이걸 가져가서 교체할 필요는 전혀 없으므로, 우선 꽉 찬 통은 모두 빼놓고 생각하자.
일단 관찰을 위해, 처음 생각한 것은 "아무렇게나 막 교환하면 꽉 찬 통을 몇 개까지 얻을 수 있을까?" 였다.
여기서 알 수 있었던 사실은, 남아 있던 용량과 관계 없이 통 3개로 무조건 꽉 찬 통 하나를 만들 수 있다는 것이다.
통 두개를 교체하면 최소 ${X \over 2}$만큼이 통에 차고, 그 통과 다른 통을 교체하면 최소 ${X \over 2} + {X \over 2} = X$만큼 차기 때문에, 최악으로 교환해도 통 3개만 있으면 통 하나를 가득 채울 수 있다.
그렇다면, 이 문제는 "통 두 개만을 사용하여 꽉 찬 통을 만들 수 있는 최대 개수 구하기" 문제로 바뀌었다.
통 두 개로 꽉 찬 통 하나를 만들기 위해서는 각 통에 들어 있던 헤어에센스의 양의 합이 ${X \over 2}$보다 많아야 하므로,
다시 한번 문제를 추상화하면 "남아 있는 용량이 ${X \over 2}$ 이상인 통의 쌍 개수를 최대화하여라." 로 바뀐다.
이제 남아 있는 용량이 ${X \over 2}$인 통 쌍 개수를 구하는 방법을 생각해야 한다.
그리고 조금 생각해보면, 남아 있는 용량이 $X$ 미만이지만 용량이 조금 많이 남은 통 두 개를 한번에 가져가서 교체하는 것은 용량 손해가 심해 보인다.
따라서, "용량이 많이 남아 있는 통은 용량이 적게 남은 통과 교체하는 것이 좋지 않을까?" 라는 생각을 할 수 있다.
즉, 최대한 용량이 많이 남아 있는 통과 최대한 용량이 적게 남은 통들 쌍 중에서 용량의 합이 ${X \over 2}$ 이상인 통들의 쌍을 투 포인터로 그리디하게 매칭하는 것이 최적이라는 가설을 세울 수 있다.
이제부터 이를 증명해보자.
오름차순으로 정렬 이후에, 가장 왼쪽의 통의 인덱스를 $l$, (가득 찬 통을 제외한)가장 오른쪽의 통의 인덱스를 $r$이라고 하자.
그러면, $C[l] \leq C[l+1] \leq C[l+2] \leq \dots \leq C[r-1] \leq C[r] < X$가 된다.
이 때, $C[l] + C[r] < {X \over 2}$라면 $C[l]$은 그 어떤 통과 더하더라도 ${X \over 2}$ 이상이 될 수 없으므로, $C[l]$은 반드시 통 세 개로만 교환 가능하다.
또한, $C[l] + C[r] \geq {X \over 2}$인 상태에서 $(C[l], C[r])$ 쌍 대신 $(C[l+1], C[r])$ 쌍을 선택하는 것은 최적이 아닌데, 만약 $C[l] + C[r] \geq {X \over 2}, C[l] + C[r-1] < {X \over 2}, C[l+1] + C[r-1] \geq {X \over 2}$라면 $(C[l], C[r]), (C[l+1], C[r-1])$ 쌍을 고를 수 있으나 $(C[l+1]+C[r])$ 쌍을 골라 버리면 $C[l]$은 절대 사용할 수 없는 통이 되기 때문에 무조건 손해가 된다.
따라서, 배열을 정렬한 뒤에 투 포인터로 "양쪽을 합해서 ${X \over 2}$ 이상이라면 $l++, r++$, 아니면 $l++$" 이라는 단순한 투 포인터 방식으로 정답을 구할 수 있다.
4. 코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
ll n, x;
ll c[100005];
int ans = 0;
cin >> n >> x;
for (int i=0; i<n; i++) {
cin >> c[i];
}
sort(c, c+n);
int l=0, r=n-1;
int left=0;
while (c[r]>=x && r>=0) {
r--;
ans++;
}
while (l<=r) {
if (l<r && c[r]+c[l]>=(x+1)/2) {
ans++;
l++;
r--;
}
else {
l++;
left++;
}
}
cout << ans+left/3;
}
5. 여담
사실 풀이 부분에서 $C[l] + C[r] \geq {X \over 2}$여야 한다고 했으나, 모든 $C[i]$는 정수로 입력되기 때문에 ${X \over 2}$에서 소수점은 아예 버려도 별로 상관이 없다.
사실 while()문 안에 l==r인 부분 예외 처리를 안해줘서 몇번 박았었는데, 다행히 빨리 찾아서 고쳤다.
아마 대회였으면 조금 더 심사숙고해서 정답을 박았겠지만... 그냥 문풀중이어서 대충 박아버리니까 좀 여러번 틀렸다.
연습 중에도 이런 습관은 좀 고쳐야겠다.
'PS > 백준 풀이' 카테고리의 다른 글
| [백준] 3307 - 대회가 끝나고 난 뒤에 빰빠빰 힌트, 풀이 및 코드(C++) (0) | 2022.07.03 |
|---|---|
| [템플릿] 백준 문제 힌트, 풀이 및 코드 템플릿 (0) | 2022.07.03 |
| [백준] 15824 - 너 봄에는 캡사이신이 맛있단다 힌트, 풀이 및 코드(C++) (0) | 2022.06.30 |
| [백준] 24916 - 용암 점프 힌트, 풀이 및 코드(C++) (0) | 2022.06.29 |
| [백준] 1800 - 인터넷 설치 힌트, 풀이 및 코드 (C++) (0) | 2022.06.29 |
디미고, 3년을 돌아보며 - 디미고 입학과 새내기 시절

제가 디미고 입학을 꿈꾸게 된건 중학교 3학년 중반쯤이었습니다.
여러 게임들을 하며 컴퓨터와 친숙해진 저는, 어느샌가 프로그래밍에 대해 찾아보게 되었고 처음 샀던 C언어 책을 바탕으로 알고리즘 문제들을 풀며 제 적성을 발견했습니다.
논리적인 과정 속에서 프로그램을 만들고, 그 프로그램이 복잡한 문제들을 빠르게 해결해 나가는 것을 보며 프로그래밍에 대해 더욱 배우고 싶다고 느끼게 되었습니다.
또, 프로그래밍을 공부하며 좋은 대학교에서 프로그래밍을 배우고 싶다는 생각까지 하며 진학할 학교를 찾아본 결과, 디미고가 가장 적합한 선택지였기에 전 디미고 입학이 가장 큰 꿈으로 다가왔었습니다.
물론 저희 중학교 선생님들과 주변 친척들은 디미고가 어떤 학교인지 정확히 몰랐기에, 제가 특성화고인 디미고에 입학한다고 하니 모두가 저를 말렸습니다.
당시 제 성적은 디미고 일반전형 150점 기준 대략 138점정도 되었고, 전교에서 10등 안에 들 성적이었던 제가 특성화고에 간다고 하니 다들 말리는 분위기였죠.
하지만 프로그래밍과 국영수 공부를 동시에, 거의 반반 비율로 하고 싶다는 제 생각을 실현시키기 가장 좋은 곳이 디미고였기에, 전 그냥 디미고에 제 3년을 맡기기로 했습니다.
또, 저희 어머니께서도 그런 저를 응원해주시며 주변 친척들을 설득하기도 해주셨구요.
하지만, 뒤늦게 디미고 진학을 희망했기에 상장이나 회장, 독서같은 생기부 점수에서 조금씩 점수가 까였기 때문에 성적이 충분히 안정권이었음에도 많이 긴장했습니다.
그렇다고 특별전형으로 지원하기엔 프로그래밍 공부가 조금 늦은 감도 있었구요.
하지만 그 생각은 기우에 가까웠고, (사실 생기부 점수가 만점인 학생은 극소수니까요..) 1차에 가볍게 합격할 수 있었습니다.
면접은 생각보다 쉬웠습니다. 사실 저도 면접에 대해, 누군가가 질문이 뭔지라도 알려줬으면 좋겠다는 생각에 죽어라 인터넷에서 검색하긴 했었지만, 면접이 끝나고 나니 "굳이..?" 라는 생각까지 들더군요.
물어보던 IT 관련 지식도 컴퓨터 앞에서 살아왔던 저에게는 그냥 아주 간단한 정도였고, 다른 생기부 관련 질문들도 시원시원하게 대답했던 것 같습니다.
그리고, 면접 때 떨리는 것도 대기실에 앉아있을 때와 면접실 앞에서 잠시 대기할 때 엄청 떨렸다가, 면접실에 들어가니 갑자기 긴장이 풀리더라구요. 그만큼 선생님들도 친절하게 대해주시기도 했구요.
사실 중학교 시절 생기부에 쓰여있던 말들이 워낙에 완벽했던 점도 선생님들께서 잘 봐주신 것 같습니다. (중학교때 선생님들이 절 좋아하시더라구요...?)
그렇게 면접이 끝나고 합격 발표날, 떨리는 마음으로 침대에 누워 합격 발표시간까지 핸드폰만 보며 누워있었고...
... 그대로 잠에 들어버렸습니다.
네, 정말 말도 안되게, 그 상태로 합격발표 시간 넘어서까지 꿀잠을 잤었습니다.
그렇게 비몽사몽한 상태로 거실에 나가니 어머니께서 먼저 합격했다는 소식을 알려주셨습니다.
뭐... 어떻게 보면 스포일러 당한 셈이죠.
전 막 합격한 순간 좋아서 엄마한테 뛰쳐 나가고... 뭐 이런걸 생각했는데 이렇게 허무하게 합격하니까 기분이 오묘하더라구요? ㅋㅋㅋ
그렇게, 전 디미고에 입학하게 되었습니다. 제가 꿈에 그리던 바로 그 디미고에 말이죠.
디미고에서의 1학년은 제가 생각한 것과 매우 유사했습니다.
대부분의 친구들이 다들 전교권에서 놀던 친구들이었고, 그런 만큼 학기 초의 학구열은 장난아니게 뜨거웠습니다.
아, 제 예상과 조금 달랐던 점이 있다면, 프로그래밍을 그렇게 잘 하는 친구가 많지는 않았던 점 정도겠네요.
그 당시 저는 C언어 포인터까지 배우고 디미고에 입학했었는데, 저만큼 알고있는 친구가 사실 상 거의 없던 정도였으니까요.
그래서 당시 프로그래밍 시간에 미리 과제를 다 끝내고 친구들을 도와주러 돌아다녔던 기억도 나네요... ㅎㅎ
디미고에서의 기숙사 생활은 생각보다 답답했습니다.
물론 어느 정도 알고 오긴 했지만, 6인 1실에 취침 시간 6시간 30분은 원체 잠이 많았던 저에겐 굉장히 무겁게 다가왔습니다.
그래서 매일 아침 (너무 싫었던) 야외 점호가 끝나고 나면, 빨리 기숙사 호실로 올라가서 아침식사 시간 바로 전까지 눈을 더 붙이기도 했었죠. (전문용어로 "리잠" 이라고 합니다 ㅋㅋ)
또, 점호 면제가 되는 날에는 기상벨을 듣고도 그냥 무시하고 계속 자던게 얼마나 꿀만 같던지...
아마 제 디미고에서의 행복한 기억 Top 50부터 대충 Top 200까지는 전부 꿀같은 리잠을 자던 기억이 아닐까 싶을 정도니까요 ㅋㅋ
그래도 다행인 점은, 취침시간을 빼고는 기숙사에서 큰 문제 일으키지 않고 잘 살았습니다.
사실 기숙사에서 저는 여기저기 돌아다니던 성격이 아니라 방에 콕 쳐박혀서 핸드폰만 하는 성격이었기에, 기숙사 규칙을 어기는 일이 있을 수가 없었죠.
물론 가끔 친구들 보러 다른 방에 들어갔다가 걸린 적도 조금은 있었지만, 그렇게 눈에 띄는 행동을 하고 다니진 않았기에 사감 선생님들도 그냥 그러려니 해 주시더라구요.
아, 그리고 기숙사 이야기 하니까 말인데, 기숙사에 벌레가 좀 많습니다.
1학년 취침 시간에 핸드폰을 신발장 위 수납함에 올려놓고 자려고 불을 끄려던 중에, 갑자기 침대에서 누가 소리를 지르며 튀어 일어나길래 뭔가 하고 봤더니, 그리마가 그 친구 이불 위에 기어다니다가 침대 아래로 떨어지더라구요...
한바탕 소동이 있고 난 뒤, 결국 청소기로 그리마를 죄다 흡수(?)하고 난 뒤에야 잘 수 있었습니다.
기숙사뿐만 아니라 학교 내부에도 벌레가 많긴 했습니다.
봄~여름쯤 화장실에 들어가보면 좌변기에 그리마 한두마리가 들어가 있는 것을 가끔 볼 수 있을 정도로 그리마는 많더군요
.처음 봤을땐 정말 혐오스러웠는데, 보다보니 귀엽기도 하고... 네, 사실상 체념한거죠.
애초에 아무리 벌레를 싫어해도 일주일에 한두마리씩 계속 보면 익숙해지는게 사람인지라... ㅋㅋㅋ
무슨 벌레얘기를 이렇게 길게 하나 싶겠지만, 그만큼 저에겐 좀 강렬한 기억이었어서 말이죠... ㅎㅎ
그리고 1학년 시기에 가장 중요한 것들 중 하나인, 동아리 가입도 생각이 나네요.
당시 게임 개발자가 되고 싶었던 저는 게임 제작 동아리 "게임즈"에 지원했고, 당시 입학 과제로 알고리즘 문제를 내던 동아리 "코인"과 이것저것 하던 동아리인 "선인장"에 지원했고, 게임즈와 선인장 동아리에 합격하게 되었습니다.
그런데 신기한 점이, 원래는 게임즈가 1지망이었는데, 이상하게 뭔가 선인장에 더 마음이 가더군요.
지금 생각해 봐도 제가 어째서 그때 게임즈를 버리고 선인장에 들어가게 되었는지는 정말 의문스럽습니다.
하지만, 이 선택은 지금 돌아와 생각해서는 제 인생을, 적어도 3년과 대학교 선택까지 바꿔놓은 큰 결과를 낳게 되었습니다.
프로젝트 동아리 선인장에 들어간 뒤, 저는 인공지능 분과를 배우기 시작했습니다.
당시 동아리에서는 대부분의 학생들의 웹을 공부했고, 1학년중에는 저와 제 친구 단 둘만이 인공지능 분과를 지원하여 공부하게 되었습니다.
3학년 선배께서 저를 가르쳐 주셨는데, 처음부터 미분의 개념이 튀어나오는 것을 보고 일종의 문화충격을 느끼게 되었습니다.
기본적인 경사 하강법 및 다층 퍼셉트론을 직접 C++로 구현하는 선배를 보고 경외심이 느껴질 정도였습니다.
그런데, 인공지능을 공부하다 보니 제 생각보다 굉장히 재미있다는 것을 발견하게 되었습니다.
원래는 인공지능이 어떻게 구현되어 있는지 전혀 몰랐는데, 인공지능이 수행하는 굉장히 복잡한 의사결정과 절차들이 결국 수학 수식과 간단한 프로그램으로 구현될 수 있다는 것을 깨달은 뒤에 인공지능에 대해 더 연구하고 싶다는 생각이 들었습니다.
인공지능 관련 공부를 더 하고싶다는 생각에 창업동아리*까지 들어가면서 인공지능을 더 배웠습니다.
인공지능 멘토 선배가 추천해준 해외 대학 강의인 CS231n을 들으며 인공지능에 대한 더 많은 지식들을 습득했고, 그것들을 풀어서 쓴 글이 제 블로그에 가장 처음 올라온 CS231n의 강의였습니다.
지금와서 돌아 생각해보니, 정말 정신없이, 무엇인가에 홀린 듯이 열심히 인공지능을 공부했던 것 같습니다.
이렇게 공부를 하며, 제가 디미고에 오기 잘했다는 생각이 계속해서 들더군요.
일반고에 갔더라면 이렇게까지 열심히, 하루종일을 써가며 내가 직접 인공지능 프로그램을 개발하고, 수정하며 개선할 수는 없었을 테니까요.
(*창업동아리: 일주일에 두번씩, 야자시간에 모여 동아리 활동을 함. 필자는 1학년 시절이었기에 창업활동에 관여는 안했고, 그냥 혼자 공부만 했었음.)
하지만 이렇게 열심히 프로그래밍과 인공지능을 공부하면서 제가 놓쳐버린 것이 하나 있었으니... 바로 내신 공부입니다.
사실 중학교때까지도 저는 내신을 아주 열심히 공부하지도 않았을 뿐더러, 디미고에 들어오니 프로그래밍이 너무나도 재밌는 나머지 공부를 조금 소홀히 하게 되었습니다.
다른 친구들이 프로그래밍과 공부를 거의 1:2 비율로 하고 있을 때, 저 혼자서 프로그래밍과 공부를 2:1 비율로 하고 있었을 정도니까요.
시험기간에도 머리를 식힌다는 핑계를 대며 알고리즘 문제들을 풀어댔었고, 주변 친구들도 저한테 시험공부 안하고 왜 코딩이나 하고 있냐고 소리 듣기 일쑤였습니다.
그러다 보니 1학년때의 시험은 잘 봤을리가 만무하고... 결국 제 성적은 나락으로 떨어지고 말았습니다.
그나마 평소에도 잘하던 수학은 2등급이라도 맞았지만, 국어와 과학이 6등급, 영어가 4등급으로 나왔으니...
국영수과가 4.5가 찍혀있는 것을 보고 정말 허탈한 마음이 들었습니다.
디미고에 들어와서 갑자기 떨어진 성적에 부모님께서 걱정하시기도 하셨지만, 그나마 모의고사 성적은 언제나 이과에서 10등 안에 들어왔기 때문에 부모님께 "저는 대학교 정시로 갈거예요" 라고 말하며 내신에 손을 놔도 된다고 어필했었죠.
지금 돌이켜 생각해보면... 정말 미친놈이 따로 없을 정도인것 같습니다.
물론 최근에야 수시가 거의 없어지고 대부분 대학을 정시로 가는 추세지만, 당시에는 연세대, 고려대 등 많은 대학들이 수시로 학생들을 모집했었기에 수시를 버리는 순간 상위권 대학을 못갔던 때였으니까요...
아무튼, 그렇게 저는 1학년 1학기 시험을 왕창 던져버리고 말았습니다.
그래도 변명이라도 좀 해보자면, 시험이 저렇게까지 망한데는 물론 제가 공부를 안한 점도 있지만, 사실 디미고 내부 분위기도 한몫 했습니다.
위에서 언급했듯 디미고에는 전교권에서 놀던 친구들만 오기에, 다들 시험기간만 되면 미친듯이 공부했습니다.
사실상 대부분의 친구들이 학기 초에는 수시를 노리며 열심히 공부하니까요..
그렇다 보니 시험에서 한두개만 틀려도 등급이 엄청 떨어졌습니다.
가령, 한국사같은 경우엔 기말에서 딱 하나 틀리고 수행평가에서 2점정도 까이니까 바로 3등급이 뜨더라구요..
(물론 국어랑 과학은 할말이 없습니다... 제가 공부를 덜해서 6등급이나 나왔어요..)
사실 그래서 1학년 1학기때부터 내신을 아예 던지고 정시파이터라는 이름으로 달리는 친구들도 생겼습니다.
저도 어찌 보면 그중 하나에 속해야 할 성적을 받았지만... 사실 전 그때는 별 생각이 없었습니다.
그저 프로그래밍이 재밌어서 즐겁게 했을 뿐이고, 내신 성적이 얼마나 중요한지도 몰랐기에 그냥 다음에는 더 열심히 공부해야겠다 정도만 생각하고, 계속 프로그래밍 공부를 해나갔습니다.
어찌 보면 이렇게 생각 없이 살았던 것이 제 디미고 3년동안의 행복의 원천이 아니었나 싶기도 하네요.
생각을 비우고 눈앞에 있던 프로그래밍과 인공지능에만 열중했던 시간들이었으니까요.
하지만 서서히 저도 디미고에 적응하고 익숙해지기 시작했고, 조금씩 더 능숙하게 생활하기 시작했습니다.
너무 과도한 프로그래밍을 줄이고, 공부에도 어느 정도 치중하기 시작했던 것이죠.
사실 1학년 1학기때는 갑자기 줄어든 취침시간이나 변화된 환경 등에 쉽사리 적응하지 못하고 방황하기 일쑤였기에, 프로그래밍과 친구관계, 시험공부를 한번에 관리할 짬이 부족했던 셈이였죠.
친구들과도 친해지고 기숙사 생활도 익숙해 지니... 그때부턴 프로그래밍과 내신 공부를 동시에 진행할 짬이 생겼습니다.
물론 그때도 수시로 대학을 가기 위해 시험공부를 했던 것은 아닙니다.
제 성격 자체가, 해야 할 일은 확실히 하고 넘어가자는 주의이기에 시험기간엔 공부를 해야지! 하며 남들 하는만큼, 또는 그것보다 조금 더 많이 공부하며 시험에 최선을 다했습니다.
특히 과학은 죽어도 1등급을 맞겠다는 생각으로 미친듯이 공부에 매달렸었습니다.
뭔가 이과가 과학을 못하면... 자존심 상하잖아요? 공부한 이유가 딱 그정도에만 머물러 있었습니다 ㅋㅋ
그 덕에, 과학을 중간/기말 모두 만점을 받고 과학 1등급을 받게 되었고, 국영수과 성적이 1학기때 4.5에서 2학기때는 2.75로 껑충 뛰게 되었습니다.
사실 국어만 더 잘봤으면 더 좋았겠지만, 1학기때부터 말아먹었던 국어실력이 2학기때라고 해서 변하지 않더라구요..
과학만큼 더 의미를 두고 공부하지 않았던 점이 더 컸겠지만요.
그러면서도 프로그래밍도 절대 놓지 않았습니다.
전 지금도 그렇지만, 프로그래밍 및 인공지능이 제 천직이라 생각하고 공부하다가 힘들거나 색다른 즐거움이 필요할 때 인강실에 들러 프로그래밍을 즐겼습니다.
가끔은 알고리즘 문제도 풀고, 인공지능 강의도 계속 듣고 블로그에 글도 쓰며 제 실력을 키워나갔습니다.
이렇게 쌓아나간 프로그래밍 실력을 원없이 뽐낼 수 있던 기회가 2학기 프로그래밍 시간에 찾아왔습니다.
프로그래밍 2학기 수행평가가 C언어로 제작하는 콘솔 게임 프로그래밍이었는데, 해당 작품을 토대로 반에서 상위 몇명만을 뽑아 본선에 나가서, 상까지 받을 수 있는 대회가 열렸기 때문입니다.
저는 제 친구와 손잡고, C언어로 스타크래프트를 구현하자는 계획을 세웠습니다.
(지금 생각하면 정말 말도 안되는 소리지만, 철없고 열정만 넘쳤던 1학년이었기에 가능한 계획이었습니다 ㅋㅋ)
스타크래프트 스프라이트를 인터넷에서 찾아내고, 음성파일이나 이미지를 스타크래프트에서 뜯어낼 수 있는 툴을 사용하셔 C언어 콘솔에 스타크래프트에 나오는 캐릭터들의 이미지와 음악 등을 재생할 수 있었습니다.
하지만 콘솔에 마우스 클릭을 통한 입력과 캐릭터 움직임까지 제작하고 나니 개발 기간이 1주밖에 남지 않더군요.
(사실 총 개발 가능 기간이 2주였습니다..)
게다가 각각의 유닛에 길찾기 알고리즘을 적용시켜 움직이게 시켜보니, 엄청나게 버벅이며 게임이 돌아갔기에 제대로 된 게임을 만들 수가 없었습니다.
당시 저와 제 친구의 알고리즘 실력으로는 효율적으로 캐릭터들을 움직이는 방식을 구현할 수가 없었기에, 그냥 스타크래프트 이미지를 씌운 유즈맵을 만들자! 로 계획이 변동되었고, 그렇게 개발된 것이 "Avoid Vulture"였습니다.
초기 게임은 무척 단순했습니다. 사방에서 날아오는 벌처를 피해 날아남기만 하면 되는 게임이었습니다.
다만, 다른 친구들이 일반적인 픽셀 게임을 만들고 있을 때, 저희들이 만들던 게임은 정말 "게임"처럼 보이는 게임이었기에, 주변 친구들에게 좋은 평을 들을 수 있었습니다.
남은 개발 기간동안 단순 탄막 게임이었던 게임에 여러가지 보스도 추가하고, 유도탄이나 핵폭발 등 다양한 기믹을 추가해 나가며 정신없이 게임을 개발했습니다.
네, 정말 정신없이 프로그래밍 했었습니다. 일주일동안 야자시간과 방과후 남는 시간에 죄다 해당 게임 개발만 했을 정도니까요.
그렇게 완성된 저희의 게임은 저희들이 봐도 꽤 훌륭한 게임의 느낌이 났고, 다른 친구들도 재미있게 플레이해 주는 것이 아주 즐거웠습니다.
그렇게 저희 게임은 반에서 높은 성적을 거두며 본선까지 진출하게 되었고, 본선에서도 1등상인 대상을 수상하게 되었습니다.
이때의 프로그래밍 경험과 수상 경험은 제게 아주 큰 기쁨을 가져다 주었습니다.
프로그래밍을 잘하는 친구들이 많은 디미고 내에서, 저와 친구의 노력과 열정으로 디미고 전체에서 최고의 게임을 개발한 팀이 되었으니까요.
또한, 프로그램을 개발하는 즐거움을 더욱 증폭시키고 타오르는 열정만으로 프로그래밍을 할 수 있었다는 사실이 정말 뿌듯하고 자랑스러웠습니다.
이는 제가 프로그래밍을 더욱 사랑하게 되는 아주 큰 계기가 되었고, 이는 앞으로 2학년과 3학년때도 제가 인공지능을 공부할 수 있던 큰 동기가 되어주었습니다.
콘솔 게임 프로그래밍 대회 대상과 썩 만족스러웠던 제 성적을 뒤로한 채, 제 1학년 시절은 이렇게 끝이 났습니다.
제가 1년간 디미고에서 배웠던 것들 중 가장 거대하고도 중요한 것은, 단연 스스로 공부하고 프로그래밍하는 즐거움이라고 생각합니다.
그 전까지만 해도 선생님께서 가르친 대로 따라가기만 하고, 책에서 알려준 대로 따라만 하는 공부만을 했다면, 인터넷 강의를 들으며 인공지능 공부를 하고, 직접 프로그램을 개발한 이 경험들은 저에게 진정한 공부란 무엇이고, 그에 따른 즐거움이 얼마나 큰지도 알려주었습니다.
제가 디미고에서 3년간 살면서 얻었던 가장 큰 원동력 중 하나인 공부의 즐거움을, 저는 1학년 이 시기에 배울 수 있었습니다.
또한, 끊임없는 노력으로, 적어도 공부만큼은 제가 원하는 대로 만들 수 있다는 것을 실감하게 된 것도 중요한 터닝 포인트였습니다.
1학기때 6등급이라는, 처참한 등급을 받고도 다시 일어나 죽어라 공부해서 1등급으로 올렸던 이 경험은 단순히 "내신 성적이 올랐다"가 아닌 더욱 큰 의미로 다가왔습니다.
스스로의 노력으로 성적을 급등시켰던 이 경험은, "나는 하면 되는 놈이다"라는 생각을 심어줌과 동시에, 앞으로 2학년과 3학년때의 제 공부에 더욱 자신감을 불어넣는 자양분이 되었습니다.
이렇게 쓰고 보니 1학년때 이야기도 엄청나게 많군요! 정말 많이도 쓴 것 같습니다.
2학년때와 3학년때의 기억보다 조금 흐릿한 기억들이 많았기에 가지치기를 많이 했어도 이정도나 나오는것을 보니, 그래도 열심히 살았던 것 같아 기분이 좋습니다.
그럼... 다음 글에서 다시 뵙도록 하겠습니다.
끝까지 읽어주셔서 감사합니다.
'일상 > 디미고' 카테고리의 다른 글
| 디미고, 3년을 돌아보며 - Intro (4) | 2021.01.31 |
|---|---|
| 디미고 진학 관련 이야기들 - 디미고 커트라인, 디미고 면접 등 (330) | 2019.11.04 |
| 디미고 입학설명회 후기 (0) | 2019.10.20 |
| 디미고 시험기간 - 최대 헬게이트, 고2 1학기 기말 (11) | 2019.06.29 |
| 디미고 일상? - 노트북 편 (8) | 2019.04.24 |
디미고, 3년을 돌아보며 - Intro

제가 디미고에 처음 입학하고 벌써 3년이라는 시간이 지났네요.
디미고 입학을 앞두고 설레하던 때부터, 수시와 정시를 동시에 준비하며 머리아파하던 때까지... 모두 새록새록합니다.
그중에서도 이 블로그는 제 디미고 인생에서 꽤 큰 부분을 차지하고 있는 것 같습니다.인공지능 공부를 시작하며 처음에는 스스로 정리하는 용도로, 또 다른 사람들에게 나의 정보를 공유하기 위해 인공지능 공부 글들도 많이 남겼었고...디미고에 입학하고 싶어하는 친구들을 위해 입학 관련 글들도 남겼었고,합격생들을 위해 학교 생활 관련 글들도 남겼습니다.그렇게 제 생각들을 하나둘씩 정리하다 보니, 제 글을 보러 오는 사람들도 하나둘씩 늘어갔습니다.
하지만 고등학교 3학년 2학기에 접어들고 부터는, 블로그에 통 글을 써보지 못했네요..수시와 정시, 두가지를 동시에 준비하며 취미인 블로그에 글 쓸 시간도 내지 못했던 셈이죠.
하지만 제 고등학교 라이프의 모든 것이 끝난 지금, 다시 제 디미고에서의 기억을 환기하며 글을 써볼 예정입니다.제가 디미고에서 어떻게 살아왔는지, 어떤 생각들을 하며 살았는지, 그리고 지금에 와서 하는 여러가지 후회들까지 전부.. 하나씩 써내려가며 제 디미고 3년의 삶을 돌아보려고 합니다.
목차는 대충 시간순이 될것 같네요.입학 전부터 1학년 새내기 시절까지 한편,정신없었고 블로그를 처음 시작하게 되었던 2학년까지 한편,그리고 코로나로 온라인 수업을 시작했고 입시가 최종적으로 종료된 3학년까지 한편, 총 3편정도가 되지 않을까 싶습니다.
... 이래놓고 한편 압축형으로 글을 쓸지도 모르겠네요...ㅋㅋ
이 글들은 디미고에 입학하기를 희망하거나 디미고가 궁금한 학생 뿐만 아니라, 이미 합격했거나 디미고에 재학중인 후배들도 위한 글이 될 예정입니다.제가 써놓은 후회들과, 정말 잘했다고 스스로 칭찬하는 것들을 보다 보면, 디미고에서 3년을 어떻게 살아야 할지 감이 오시리라 생각됩니다.
사실 저는 제 친구들과 가족들에게 언제나 말하고 다니는 것 처럼, 제가 디미고에서 가장 행복하고, 만족스럽게 학교생활을 해나간 사람이라고 생각합니다.하지만, 저와는 다르게 제 주변에 디미고에서의 생활을 힘들어하던 친구들도 더러 있었습니다.이 글들에서는 디미고 입학에 관심있으신 분들을 위해서도, 과연 어떤 사람이 디미고에 와야 하는가에 대한 이야기도 할 예정입니다.행복하고 만족스러운, 그러면서도 어쩌면 가장 성공적인 디미고 3년을 위해 어떤 마음가짐을 가지고 어떤 행동을 해야 하는가... 에 대한 이야기지요.또, 아마 가장 많은 분들이 궁금해 할만한 디미고에서의 대학 입시와 입결과 같은 이야기들도 3편에서 중점적으로 하게 되지 않을까 싶습니다.
뭔가 써놓고 보니 글이 두서도 없고 이것저것 막 써놓은것 같네요... ㅋㅋ뭐, 아무튼... 이제부터 글 한번 써보도록 하겠습니다!
'일상 > 디미고' 카테고리의 다른 글
| 디미고, 3년을 돌아보며 - 디미고 입학과 새내기 시절 (51) | 2021.01.31 |
|---|---|
| 디미고 진학 관련 이야기들 - 디미고 커트라인, 디미고 면접 등 (330) | 2019.11.04 |
| 디미고 입학설명회 후기 (0) | 2019.10.20 |
| 디미고 시험기간 - 최대 헬게이트, 고2 1학기 기말 (11) | 2019.06.29 |
| 디미고 일상? - 노트북 편 (8) | 2019.04.24 |
딥러닝 직접 구현하기 프로젝트 3-2차시: Im2col과 효율적인 Convolution 연산
* 모든 코드는 제 깃허브 (cdjs1432/DeepLearningBasic: Deep Learning from scratch)에서 확인할 수 있습니다.
이번 시간에는 Convolution 연산 (Forward, Backward)에 대해 다뤄보겠습니다.
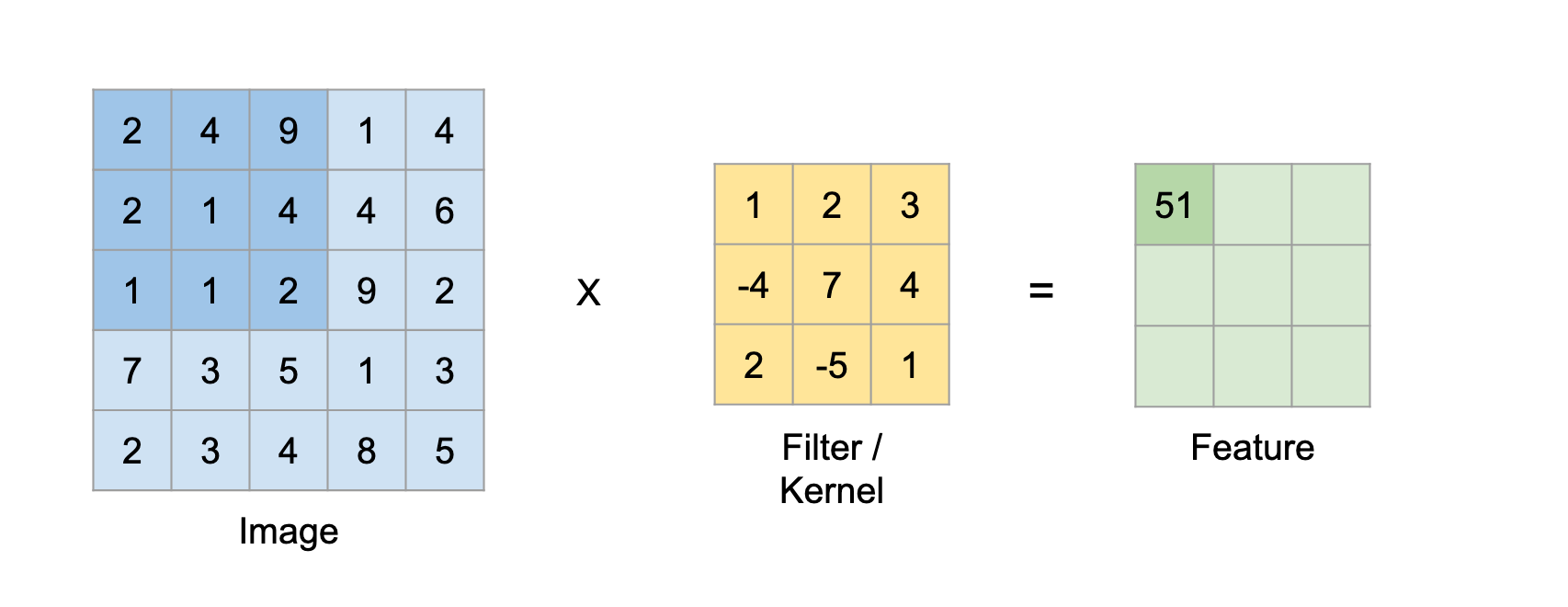
Convolution 연산은 본질은 굉장히 단순합니다. filter를 왼쪽에서 오른쪽으로, 위에서 아래로 이미지에 대고 점곱을 하면 되기 때문입니다.
하지만, 이는 생각보다 그리 단순하지 않습니다.
우선, 위의 이미지의 경우는 단순히 1장의 1-Channel 이미지의 예시이기 때문에 간단하게 대략 이미지의 크기만큼만 연산을 해 주면 됩니다.
하지만, 우리가 train할 때 사용하는 이미지는 4차원 (batch_size, channel, h, w)이므로 연산이 매우 복잡해 집니다.
예를 들어, 위의 2차원 이미지는 단순히 2중 for문으로 구현이 가능하지만, 4차원의 경우에는 4중 for문이 필요하게 됩니다.
또, 시간 복잡도도 너무 커집니다.
저번 차시에 썼던 out_h, out_w를 가져와서 설명해 보겠습니다.
간단하게 생각해서, pad=0, stride=1인 경우, out_w는 1 + w - fw가 되고, out_h는 1 + h - fh가 됩니다.
이 때, 이미지 크기 h, w에 대하여, 단 한 장의 2차원 이미지의 연산을 위해서 out_w * out_h만큼의 점곱 연산이 필요합니다.
MNIST dataset의 이미지 크기가 28*28인 것을 생각해 보면, (3, 3) 필터를 사용하였을 경우 단 한장의 이미지의 convolution을 위해서는 무려 26*26, 즉 676회의 점곱 연산이 필요합니다.
만약 50000개의 이미지 전체를 모두 Convolution 연산을 한다면, 676*50000, 즉 33,800,000회라는 무시무시한 양의 연산이 필요하게 됩니다.
만약 Convolution Layer가 두개가 겹쳐져서 Channel이 32개가 되었다면? 저 횟수의 32배를 연산해야 하는 것이죠.
게다가 컴퓨터 (또는 numpy libarary)는 점곱 연산은 아주 빠르게 수행하지만, 해당 점곱을 각각의 배열에 집어넣고 더하고... 하는 과정은 상대적으로 느리게 수행됩니다.
따라서, 점곱 연산의 횟수를 줄이는 것이 시간 복잡도와, 우리 코드의 복잡도 모두를 해결할 수 있습니다.
그렇다면 어떻게 시간 복잡도를 최적화 할 수 있을까요? 잠시 생각해 봅시다.
우선, 위 연산의 본질을 생각해 봅시다.
필터의 각각의 부분 (위 이미지에선 1, 2, 3, -4, 7, 4, 2, -5, 1)은 사실, 이미지의 특정 픽셀들과만 연산을 하게 됩니다.
가령, 필터 왼쪽 위 1은 이미지의 우측 하단 부분을 아예 연산하지 않습니다.
즉, filter의 각 부분은 애초에 이미지의 어떤 부분과 곱셈을 수행하는지 정해져 있다는 것입니다.
그렇다면, filter의 각 부분에 연산해야 할 부분만을 빼서, 각 필터와의 단 한번의 곱셈으로 바꾸면 어떨까요?
filter의 각 부분에 해당하는 부분들을 각각 배서, filter와의 점곱으로 연산을 하면 단 한번의 점곱으로 마무리 지을 수 있지 않을까요?

해당 방식을 구체화 한 것이 바로 Im2col 알고리즘입니다.
Im2col 방식은, 말 그대로 Image를 Column으로 바꾸는 알고리즘입니다.
4차원 이미지인 input image와 filter를 둘 다 2차원 행렬로 만들어서, 점곱으로 연산이 가능하게 하는 것입니다.
위 이미지를 예시로 설명하겠습니다.
위 이미지에서는 빨간색, 초록색, 파란색으로 channel을 구분하고 있습니다.
첫 번째 channel의 filter인 F0은 D0, D1, D3, D4와만 연산이 되니, 해당 이미지 값들을 빼서 하나의 Column으로 만들어 줍니다.
이 행동을 모든 filter F0, F1, F2, F3에 반복해 줍니다.
그렇게 하면 오른쪽처럼 이미지의 Column이 생성됩니다.
또, 이를 각각의 filter마다, 각각의 channel마다 반복해 주면, 행렬 두개가 만들어지게 됩니다.
(참고로, 모든 필터의 각각의 부분은 모두 동일한 부분과만 연산하므로, filter의 행렬은 filter를 reshape한 것과 동일한 결과가 나오게 됩니다.)
이 방법은 사실, 원래 단 한번씩만 등장하던 이미지의 픽셀값이 여러 번 중복되어 여러번 나타나기 때문에 공간 복잡도가 커지게 된다는 단점이 있습니다.
하지만, 그렇게 해서 낭비되는 공간보다 아낄 수 있는 시간 복잡도가 훨씬 높기에(원본 conv의 약 200배 속도), 이 방식은 자주 사용됩니다.
이제, 이 Im2col 함수를 코드로 구현해 볼까요?
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
return col코드를 살펴봅시다.
우선, input data에서 이미지의 개수, channel, 그리고 가로세로 길이를 구한 뒤 out_h, out_w를 지정해 줍니다.
그 뒤, input_data에 padding을 해 줍니다. (np.pad...)
다음으로, 이미지의 행렬을 담을 col을 ((이미지 크기, channel, filter 세로, filter 가로, out 세로, out 가로))의 크기로 만들어 줍니다.
이 크기로 만들어 주는 이유는, 어차피 모든 이미지 개수(N)와 channel(C)마다 동일한 연산을 해 줄 것이고, filter 하나의 행렬의 크기가 바로 (filter_h, filter_w)이기 때문입니다.
그리고, filter_h와 filter_w의 크기에 대하여, for loop를 돌아줍니다.
각 filter의 원소마다 연산해 줄 이미지를 추출하기 위함입니다.
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]가 바로 이미지를 추출하는 부분입니다.
y:y_max:stride는, y에서부터 y_max까지, stride식 건너뛰면서 index를 추출하라는 의미입니다.
(참고로, col의 순서를 위처럼 한 것도 이런 대입 연산이 필요하기 때문입니다.)
마지막으로, 이 column을 reshape해주기 위해 transpose해 줍니다.
이렇게 transpose하지 않으면 reshape 시에 원래 우리가 의도했던 행렬이 아니라, 어딘가 뒤틀린 행렬이 됩니다.
이렇게 만들어진 col을 return하면, 이 함수의 일이 끝나게 됩니다.
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_shape
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
이 im2col의 자매품? 으로, col2im이라는 함수도 있습니다.
Convolution의 backward 연산에 활용되는 함수로, im2col로 만들어진 column에서 원본 이미지로 바꿔주는 함수입니다.
위의 im2col을 거의 그대로 반대로 했을 뿐이므로, 설명은 생략하겠습니다.
이렇게, Convolution 연산의 준비가 모두 끝났습니다! 이제 직접 Convolution 연산을 구현해 봅시다.
def forward(self, x):
# Convolution Calculation
self.x = x
fn, fc, fh, fw = self.param.shape
n, c, h, w = x.shape
out_h = int(1 + (h + 2 * self.pad - fh) / self.stride)
out_w = int(1 + (w + 2 * self.pad - fw) / self.stride)
# Conv Input Size: (Channel, Filter_num, kernel_h, kernel_w)
# Change this using im2col
col = im2col(x, self.kernel_size[0], self.kernel_size[1], self.stride, self.pad)
col_param = self.param.reshape((fn, -1)).T
self.col = col
self.col_param = col_param
out = np.dot(col, col_param)
out = out.reshape(n, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out윗부분 (~out_w... 부분까지)는 지금까지 계속 설명해 왔던 것이므로 설명을 생략하고, 연산 부분만 간단히 보겠습니다.
우선, im2col 함수를 활용하여 input_data인 x를 column으로 바꿔 줍니다.
그리고, Convolution parameter, 즉 filter 또한 행렬로 바꿔주어야 합니다.
그런데 이 연산은 매우 간단하게 수행이 가능한데, 위에서 봤듯이 filter의 경우는 그냥 filter의 개수만큼 쭉 펴주기만 하면 됩니다.
그리고 그냥 점곱을 한번 해 주면, 간단하게 output 값이 나오게 됩니다.
이제, 이 output 값을 원래 크기대로 reshape 및 transpose해주기만 하면, forward 연산은 종료됩니다.
def backward(self, dout):
fn, c, fh, fw = self.param.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, fn)
self.grad = np.dot(self.col.T, dout)
self.grad = self.grad.transpose(1, 0).reshape(fn, c, fh, fw)
dcol = np.dot(dout, self.col_param.T)
dx = col2im(dcol, self.x.shape, fh, fw, self.stride, self.pad)
return dx
backward 연산도 비교적 간단합니다.
forward와 반대로, 들어온 dout 값을 transpose한 뒤 reshape해 줍니다.
그리고, MulLayer의 backward함수와 동일하게 (어차피 곱하기만 하므로...) grad를 구해주면 됩니다.
사실 연산 자체는 점곱을 하는 MulLayer와 동일하지만, 단지 transpose와 reshape, col2im만 더해졌다고 보면 됩니다.
이렇게, Convolution Layer의 forward와 backward 연산을 마칩니다.
다음 시간에는 Pooling Layer (Maxpooling, Average Pooling...)을 구현해 보겠습니다.
'인공지능 > 딥러닝 직접 구현하기 프로젝트' 카테고리의 다른 글
| 딥러닝 직접 구현하기 프로젝트 3-1차시: Convolution Layer 틀 잡기 (0) | 2020.08.11 |
|---|---|
| 딥러닝 직접 구현하기 프로젝트 2-7차시 - 코드 정리 + Model Save / Load (0) | 2020.08.01 |
| 딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃 (0) | 2020.07.29 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Gradient Descent Optimizer 구현하기 (2) (2) | 2020.07.07 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Optimizer (Momentum, NAG) 구현하기 (1) (4) | 2020.06.30 |
딥러닝 직접 구현하기 프로젝트 3-1차시: Convolution Layer 틀 잡기
* 모든 코드는 제 깃허브 (cdjs1432/DeepLearningBasic: Deep Learning from scratch)에서 확인할 수 있습니다.
이번 시간부터는, Convolutional Neural Network를 구현해 보겠습니다.
그리고 이번 차시에서는 우선 간단하게 Convoluton Layer을 구현해 보도록 합시다.

Convolution Layer는 일반적으로는 5*5, 3*3, ... 정도의 크기를 가진 filter를, 대략 32개, 64개, ... 만큼 가지게 됩니다.
원래의 Mul Layer이나 Add Layer들이 1차원 크기의 parameter를 가진 것과 다르게, 이 친구는 무려 3차원 크기 (channel도 고려하면 4차원 크기)의 parameter를 가지게 됩니다.
그 점을 반영해서, 일단 ConvLayer의 Init부분부터 짜봅시다.
class ConvLayer:
def __init__(self, filters, kernel_size, stride=1, pad=0, initializer='he', reg=0):
self.activation = False
self.reg = reg
self.x = None
self.param = None
self.grad = None
self.stride = stride
self.pad = pad
self.init = initializer
self.kernel_size = kernel_size
self.filters = filters
self.col = None
self.col_param = None
if type(kernel_size) == int:
kernel_size = (kernel_size, kernel_size)
self.out = (filters, *kernel_size)원래 다른 Layer이 공통적으로 가지는 reg, x, ... 등을 제외하고, 지금 단계에서 봐야 할 변수들은 (일단은) kernel_size, filters, self.out이 되겠습니다.
kernel_size는 Convolution Layer의 크기를 의미하고, filters는 filter의 개수를 의미합니다.
저 아래 if type... 부분은, kernel_size를 int형으로 입력했을 경우 out을 제대로 넣기 위한 부분입니다.
보통 conv layer는 3*3, 4*4... 와 같이 정사각형 모양이기에, 저렇게 input을 받아도 되도록 만들어 두었습니다.
self.out은 parameter가 가지는 shape를 의미합니다.
다음은, train 함수에서 이 Layer가 연산되기 위해 parameter size를 변환하는 코드를 보겠습니다.
def train(self, x_train, y_train, optimizer, epoch, learning_rate, skip_init=False):
if not skip_init:
in_size = x_train.shape[1:]
for name in self.layers:
if not self.layers[name].activation:
out_size = (self.layers[name].out,)
if isinstance(self.layers[name], ConvLayer):
out_size = out_size[0]
fn, fh, fw = out_size
c, h, w = in_size
size = (fn, c, fh, fw)
out_h = int(1 + (h + 2 * self.layers[name].pad - fh) / self.layers[name].stride)
out_w = int(1 + (w + 2 * self.layers[name].pad - fw) / self.layers[name].stride)
in_size = (fn, out_h, out_w)코드를 잠깐 설명해 보겠습니다.
우선, out_size[0]은 아까 받았던 self.out을 꺼내줍니다.
그러면, filter의 개수, filter의 높이, filter의 너비를 알 수 있습니다.
또한, in_size 안에는 input image의 channel, 높이, 너비를 알 수 있습니다.
그리고, 우리는 필터의 크기를 (filter 개수, channel, 높이, 너비)로 만들 것입니다.
(참고: channel을 위처럼 앞에 놓는 것을 channel_first라 하고, (fn, fh, fw, c) 처럼 뒤에 놓는 것을 channel_last라고 합니다. 이번 구현에선 channel_first로 구현합니다.)
다음은 out_h, out_w입니다.
위 out_h, out_w는 Convolution 연산 이후에 나오는 output의 크기입니다.
아직 우리는 padding layer와 stride를 구현하진 않았으나, 그냥 있는 셈 치고 out_h와 out_w를 계산해 봅시다.
이미지의 가로 크기를 w, filter의 가로 크기를 fw라 해 봅시다.
만약 이미지를 padding한다면 가로 크기는 w + 2*pad가 될 것이고, stride=1인 상태라면 연산 횟수는 1 + w + 2*pad - fw가 될 것입니다.
하지만 여기서 stride까지 생각해 준다면, 연산 횟수는 stride의 크기만큼 나눠준 값으로 바뀔 것이므로,
stride를 포함한 연산 횟수는 1 + (w + 2 * pad - fw) / stride가 됩니다.
그리고, output의 크기는 연산 횟수와 동일하므로, out_w는 위의 식으로 정리가 됩니다.
마찬가지의 방식으로, out_h도 동일하게 계산이 가능합니다.
그 뒤, 다음 layer가 받을 in_size의 크기를 (fn, out_h, out_w)로 두면서 size 연산을 끝내 줍니다.
그런데, 이렇게 연산을 하기 위해서는, Flatten Layer도 필요합니다.
사실 지금까지는 우리가 이미 Flatten된 MNIST dataset을 사용하고 있었기 때문에 Flatten Layer가 필요하지 않았지만, Convolution Layer를 구현하기 위해선 Flatten Layer가 필요합니다.
4차원의 이미지를, Fully-connected Layer 및 Softmax 함수가 받을 수 있게 1차원 벡터화 시키는 것입니다.
Flatten 구현은 간단하니 지금 바로 해봅시다.
class Flatten:
def __init__(self):
self.shape = None
self.activation = True
def forward(self, x):
return x.reshape(x.shape[0], -1)
def backward(self, dout):
return dout.reshape(-1, *self.shape)
예, 그렇습니다. forward와 backward는 그저 받았던 input을 1차원으로 바꿔주고, 돌아오는 dout을 원래 형태로 펴주기만 하면 됩니다.
그러기 위해서, self.shape를 만들어서 train 전처리 과정에서 shape를 지정해 주도록 합시다.
elif isinstance(self.layers[name], Flatten):
self.layers[name].shape = in_size
tmp_size = 1
for items in in_size:
tmp_size *= items
in_size = (tmp_size,)(Model.py - train함수 - if not activation 뒷부분)
Flatten 함수는 이전 Layer의 input size - in_size를 shape로 가지게 됩니다.
그리고, 해당 shape를 가졌을 때의 1차원 벡터의 크기는 shape에 있는 모든 원소의 곱이므로, shape의 원소를 죄다 곱해 줍니다.
그리고 해당 값을 다음 layer의 in_size로 바꿔주면 끝입니다.
이제 Convolution Layer의 연산을 다룰 차례입니다만, 이 부분은 다음 포스트에서 더 자세히 다루도록 하겠습니다.
Convolution Layer의 연산이 그렇게까지 단순하게 이뤄지진 않기 때문입니다. (물론, 그냥 곱셈이긴 하지만 말이죠...)
'인공지능 > 딥러닝 직접 구현하기 프로젝트' 카테고리의 다른 글
| 딥러닝 직접 구현하기 프로젝트 3-2차시: Im2col과 효율적인 Convolution 연산 (5) | 2020.08.11 |
|---|---|
| 딥러닝 직접 구현하기 프로젝트 2-7차시 - 코드 정리 + Model Save / Load (0) | 2020.08.01 |
| 딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃 (0) | 2020.07.29 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Gradient Descent Optimizer 구현하기 (2) (2) | 2020.07.07 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Optimizer (Momentum, NAG) 구현하기 (1) (4) | 2020.06.30 |
딥러닝 직접 구현하기 프로젝트 2-7차시 - 코드 정리 + Model Save / Load
* 모든 코드는 제 깃허브 (cdjs1432/DeepLearningBasic: Deep Learning from scratch)에서 확인할 수 있습니다.
이번에는 다음에 구현할 CNN의 구현을 위해, 코드를 예쁘게 바꿔 보는 시간을 가져보겠습니다.
당연히, 다른 이론 설명은 없습니다.
오늘 코드 정리의 첫 번째 목표는, 바로 모델 코드를 다음과 같이 바꾸는 겁니다.
model = Model()
model.addlayer(Layers.MulLayer(100, initializer='he', reg=0.01), name="w1")
model.addlayer(Layers.AddLayer(100), name='b1')
model.addlayer(Layers.ReLU(), name='relu1')
model.addlayer(Layers.Dropout(), name='dropout1')
# ...어떻게 바뀌었나 잠깐 보면, 원래는 addlayer의 인자로 input_size를 주었다면, 이제는 Layers의 인자로 output_size만을 주게 됩니다.
또한, 그것 말고도 다른 initializer이나 regularizer 등도 Layer 안에 들어가게 되겠습니다.
이제 Layer에서, 어떻게 설계를 변경했는지 보겠습니다.
class MulLayer:
def __init__(self, out, initializer='he', reg=0):
self.x = None
self.out = out
self.param = None
self.grad = None
self.init = initializer
self.reg = reg
self.activation = False
def forward(self, x):
self.x = x
return x.dot(self.param)
def backward(self, dout):
self.grad = np.dot(self.x.T, dout)
return np.dot(dout, self.param.T)
(MulLayer과 Addlayer은 거의 동일하니 같이 설명하겠습니다.)
우선, MulLayer의 init에서 initializer, regularizer과 함께 activation function인지 아닌지 체크하는 변수가 들어가겠습니다.
이를 통해, layer의 선언만으로 initializer, regularizer를 확실히 설정할 수 있고, activation인지 아닌지를 굳이 함수 입력 시에 넣지 않아도 되게 만들었습니다.
그 외의 forward, backward는 동일합니다.
다음으로는, parameter의 초기화를 하게 됩니다.
이 parameter 초기화는 원래 addlayer에서 이뤄졌었으나, 이제는 input data가 입력되는 train에서 하게 되겠습니다.
def addlayer(self, layer, name=None):
if name is None:
name = str(self.num)
self.keys.append(name)
self.num += 1
self.layers[name] = layer그 결과, addlayer은 다음과 같이 다이어트를 감행하게 되었습니다.
parameter의 선언부는 다 지우고, layers와 keys에 집어넣는 것들만 남게 되었습니다.
def train(self, x_train, y_train, optimizer, epoch, learning_rate):
in_size = x_train.shape[1:]
for name in self.layers:
if not self.layers[name].activation:
out_size = self.layers[name].out
if type(in_size) is int:
size = (in_size, out_size)
else:
size = (*in_size, out_size)
self.weight_decay_lambda[name] = self.layers[name].reg
if isinstance(self.layers[name], AddLayer):
self.params[name] = np.zeros(self.layers[name].out)
elif self.layers[name].init is 'xavier':
self.params[name] = xavier_initialization(size)
elif self.layers[name].init is 'he':
self.params[name] = he_initialization(size)
else:
self.params[name] = np.random.uniform(size)
in_size = out_size
self.layers[name].param = self.params[name]
optimizer.train(x_train, y_train, epoch, learning_rate, self)
마지막으로, train 함수입니다.
이 부분에서 처음으로 input data가 들어오므로, 여기에서 parameter initialize를 하겠습니다.
코드를 대충 설명해 보자면...
우선, input size는 처음에 x_train.shape[1:] (이미지 개수를 제외한 픽셀 수)와 동일합니다.
그리고, out_size는 layer에서 이미 선언해 주었으므로, 그대로 가져옵니다.
여기서, in_size가 튜플로 들어올 수도 있고, int로 들어올 수도 있습니다.
단순한 MulLayer, AddLayer을 지나왔다면 int, 픽셀 개수 (ex: (28, 28))로 그대로 들어온다면 튜플로 들어오겠습니다.
그래서, 이를 체크해 주며 parameter의 size를 결정해 주었습니다.
그 외의 나머지 부분은 다 비슷합니다.
다음 목표는, model save / load 기능 구현과 Model의 일부 변경입니다.
코드가 워낙 많이 바뀌어서, 그냥 바뀐 부분은 간결하게만 짚고 넘어가고, load/save 함수 중심으로 설명하겠습니다.
def save(self, path=''):
f = open(path + "model.txt", 'w')
f.write(path + "weight.npz\n")
params = {}
for name in self.layers:
data = self.layers[name].__class__.__name__ + "\n" + name + "\n"
if not self.layers[name].activation:
params[name] = self.layers[name].param
f.write(data)
np.savez(path + "weight", **params)
def load(self, path):
f = open(path)
weight_path = f.readline()[:-1]
load = np.load(weight_path)
while True:
layer = f.readline()[:-1]
if not layer:
break
name = f.readline()[:-1]
self.addlayer(eval(layer)(), name)
if name in load:
self.layers[name].param = load[name]
save함수는 위와 같이 구현했습니다. (Model.py)
path가 주어지면, 해당 path에 model.txt와 weight.npz를 생성합니다.
model.txt에는 model의 전체적인 구조를 저장하고, weight.npz는 가중치의 numpy 배열을 저장합니다.
그리고, npz에 한번에 저장하기 위해 params dictionary를 생성해 줍니다.
그 뒤, self.layers에서 각각의 layer의 class명과, name을 하나씩 저장해 줍니다.
그러는 와중에, params에는 각각의 가중치값을 저장합니다.
그리고, 마지막으로 np.savez함수로 지금까지 모았던 params를 한번에 저장합니다.
load 함수는 이와 정 반대로 일어납니다.
weight_path(weight.npz 파일 경로)에서 np.load를 통해 numpy array를 불러옵니다.
그리고, model.txt를 읽어오면서 각각의 layer를 생성하고, 그 안에 불러왔던 array를 param에 넣습니다.
이렇게 지금까지 학습했던 가중치를 가져올 수 있습니다.
이 함수를 만들면서 바꿔야 했던 함수들이 몇 개 있습니다.
간결하게 짚고만 넘어가겠습니다.
class AddLayer:
def __init__(self, out=None, initializer='he', reg=0):
# ...
class MulLayer:
def __init__(self, out=None, initializer='he', reg=0):
# ...(Layers.py)
우선, AddLayer와 MulLayer에 out(즉, size)가 들어오지 않을 수 있습니다.
out=None으로 설정해 줘서, out size 없이도 load할 수 있도록 만들었습니다.
def train(self, x_train, y_train, optimizer, epoch, learning_rate, skip_init=False):
if not skip_init:
# ...(Model.py)
그리고, train에서의 init을 skip할 수 있도록 위와 같이 함수를 선언했습니다.
이제, train의 마지막 부분에 True를 넣으면 변수를 원래 가지고 있던 그대로 학습시킬 수 있습니다.
def forward(self, x, train_flag=True):
for i in range(len(self.keys) - 1):
key = self.keys[i]
if isinstance(self.layers[key], Dropout):
x = self.layers[key].forward(x, train_flag)
else:
x = self.layers[key].forward(x)
if key in self.weight_decay_lambda:
self.l2[key] = np.sum(np.square(self.params[key])) * self.weight_decay_lambda[key]
return x
def predict(self, x):
x = self.forward(x)
self.pred = softmax(x)
return self.pred
def eval(self, x, y, epoch=None):
x = self.forward(x, False)
self.loss = self.layers[self.keys[-1]].forward(x, y)
self.loss += sum(self.l2.values()) / 2
self.pred = softmax(x)
if epoch is None:
print("ACC : ", (self.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS : ", self.loss)
else:
print("ACC on epoch %d : " % epoch, (self.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS on epoch %d : " % epoch, self.loss)
(Model.py)
또, 원래 predict였던 함수를 forward / predict / eval 로 나누어 주었습니다.
predict는 input의 정답을 예측하는 함순데, 지금까지 y를 넣지 않으면 작동하지를 않았거든요..
위와 같이 바꿔줌으로써, 이미지만 넣어도 예측을 할 수 있도록 바뀌었습니다.
또한, eval 함수를 새로 만들어서 간단하게 loss와 acc를 알 수 있도록 하였습니다.
위 두 함수, predict와 eval에서 겹치는, 첫 x값을 마지막 layer까지 순전파법으로 가져가는 부분은 forward 함수로 따로 뺐습니다.
def train(self, x_train, y_train, epoch, learning_rate, model):
for epochs in range(epoch):
batch_mask = np.random.choice(x_train.shape[0], self.batch_size)
x = x_train[batch_mask]
y = y_train[batch_mask]
z = model.forward(x)
model.loss = model.layers[model.keys[-1]].forward(z, y)
model.loss += sum(model.l2.values()) / 2
dout = model.layers[model.keys[-1]].backward()
for i in reversed(range(len(model.keys) - 1)):
key = model.keys[i]
dout = model.layers[key].backward(dout)
if key in model.params:
model.grads[key] = model.layers[key].grad + model.weight_decay_lambda[key] * model.params[key]
model.params[key] -= learning_rate * model.grads[key]
if epochs % (epoch / 10) == 0:
model.eval(x, y, epoch=epochs)
model.eval(x_train, y_train)(Optimizer.py - SGD)
바뀐 부분은, z = model.forward와 그 밑 두줄, 그리고 가장 아래의 model.eval()입니다.
SGD뿐만 아니라 다른 optimizer들에도 동일하게 적용하면 되겠습니다.
이렇게 코드 정리와 Model Save/Load를 구현해 보았습니다.
다음 차시부터는 CNN을 구현해 보도록 하겠습니다.
'인공지능 > 딥러닝 직접 구현하기 프로젝트' 카테고리의 다른 글
| 딥러닝 직접 구현하기 프로젝트 3-2차시: Im2col과 효율적인 Convolution 연산 (5) | 2020.08.11 |
|---|---|
| 딥러닝 직접 구현하기 프로젝트 3-1차시: Convolution Layer 틀 잡기 (0) | 2020.08.11 |
| 딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃 (0) | 2020.07.29 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Gradient Descent Optimizer 구현하기 (2) (2) | 2020.07.07 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Optimizer (Momentum, NAG) 구현하기 (1) (4) | 2020.06.30 |
딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃
* 모든 코드는 제 깃허브 (cdjs1432/DeepLearningBasic: Deep Learning from scratch)에서 확인할 수 있습니다.
저번 시간에 optimizer를 만들며 기본적인 딥 러닝 함수들은 모두 만들었습니다.
저 함수들만 사용하더라도 꽤나 좋은 인공지능을 제작할 수 있겠죠.
하지만, 이번 시간에는 여기서 조금 더 나아가서 인공지능의 정확도를 더욱 높일 수 있는 방법들에 대해 설명하고, 구현해 보겠습니다.
가장 먼저 구현할 것은, 가중치의 초기화입니다.
지금까지 보신 분들은 아시겠지만, 지금까지는 가중치 초기화를 단순히 랜덤값으로 선언했었습니다.
하지만, 이렇게 단순 랜덤으로 가중치를 초기화하면 Vanishing Gradient가 발생할 가능성이 매우 커집니다.
Vanishing Gradient란, 딥 러닝에서 많은 레이어들을 거치며 가중치에 값을 곱하고 활성화 함수를 거치는 과정에서, 다수의 Gradient들이 0으로 수렴하게 되는 현상을 의미합니다.
그 뿐만 아니라, 가중치를 너무 크게 초기화하면 레이어들을 거치며 Gradient가 무한으로 발산하는 경우도 발생할 수 있습니다.
또한, Sigmoid함수의 경우는 Saturation이라는 문제도 발생합니다.
이는 Gradient의 값의 범위가 너무 클 때 생기는 문제인데, Sigmoid의 경우 값이 너무 작으면 0에 수렴하고, 값이 너무 크면 1에 수렴하는 특징을 가지고 있습니다.
하지만 만약 가중치의 값을 -1 ~ 1로 초기화를 해 버리면, 들어오는 데이터에 따라 w*x의 값이 매우 커질수도 있습니다.
만약 이미지의 크기가 10*10이고, 모든 이미지 픽셀이 1이고 가중치도 1이라면, w*x는 최대 100이라는 수치가 나옵니다.
이러한 Gradient는 어떻게 해도 1에 수렴하게 되기 때문에, 학습에 아무런 도움도 주지 않습니다.
반대로, 가중치가 -1이었다면 w*x는 최소 -100이라는 수치가 나오게 되고, 그러면 마찬가지로 Gradient가 0으로 수렴하게 됩니다.
Xavier Initialization은 이러한 Saturation의 문제점을 해결할 수 있는 Initialization 방법 중 하나입니다.
이 방식은 w*x의 값의 범위를 -1~1로 제한해줄 뿐만 아니라, 앞 레이어와 뒤 레이어의 분산까지 맞춰줌으로써 학습이 더욱 원활하게 되게 해 줍니다.
이론적인 이야기는 여기까지만 하고, 바로 구현에 들어가 봅시다.
def addlayer(self, layer, activation=False, input_size=None, name=None, initialization=None):
if name is None:
name = str(self.num)
self.keys.append(name)
self.num += 1
self.layers[name] = layer
if not activation:
if isinstance(layer, AddLayer):
self.params[name] = np.zeros(input_size)
elif initialization is 'xavier':
self.params[name] = xavier_initialization(input_size)
else:
self.params[name] = np.random.uniform(-1, 1, input_size)
self.layers[name].param = self.params[name]Model.py의 addlayer 부분입니다.
initialization이 'xavier'로 선언되었을 경우에 xavier_initialization으로 가중치 값을 초기화 하게 됩니다.
또한, AddLayer, 즉 bias의 경우는 처음부터 그냥 0으로 초기화해 주었습니다. (원래 bias는 random 초기화를 하지 않습니다)
def xavier_initialization(input_size):
fan_in = input_size[0]
fan_out = input_size[1]
n = np.sqrt(6 / (fan_in + fan_out))
w = np.random.uniform(-n, n, input_size)
return w
다음은 위에서 사용한 xavier_initialization 함수 내부입니다.
uniform xavier 공식을 그대로 사용했습니다. (공식 유도까지 하면 너무 오래 걸리는 관계로 생략하겠습니다.)
또한, 위에서 언급한 Xavier initialization은 보통 activation function, 즉 활성화 함수가 sigmoid함수일 때 자주 사용합니다.
활성화 함수가 ReLU일 때는, He Initialization을 사용하는데, 크게 달라지는 점은 없으니 그냥 바로 코드로 넘어가겠습니다.
if not activation:
if isinstance(layer, AddLayer):
self.params[name] = np.zeros(input_size)
elif initialization is 'xavier':
self.params[name] = xavier_initialization(input_size)
elif initialization is 'he':
self.params[name] = he_initialization(input_size)
else:
self.params[name] = np.random.uniform(-1, 1, input_size)
self.layers[name].param = self.params[name]...그냥 아까 윗부분에서 elif ... he: 부분만 추가했고,
def he_initialization(input_size):
fan_in = input_size[0]
n = np.sqrt(6 / fan_in)
w = np.random.uniform(-n, n, input_size)
return wxavier_initialization 아래 부분에 그냥 하나 새로 만들었습니다.
이제, 이렇게 함으로써 다층 Neural Network를 구현할 때에도 Vanishing Gradient나 Saturating 현상이 덜 일어나게 될 것입니다.
다음으로, 정규화 (Regularization)을 구현해 보겠습니다.
Regularization이란, 인공지능의 Overfitting을 막기 위해 사용되는 기법으로, 너무 특정 데이터들에만 강력하게 학습되는 것을 막기 위한 장치입니다.
Regularization에는 여러 가지 종류 (L1, L2 ...) 등이 있는데, 이번 포스팅에서는 L2 Regularization에 대해서만 다루겠습니다.
(다른 Regularization은 직접 구현해 보세요!)

Regularization은 Loss값에 W(가중치)에 비례한 값을 더해서 overfitting을 막는 기법입니다. (L2의 경우, W^2에 비례합니다.)
즉, W값이 크다면 그만큼 Loss값은 커지고, W값이 작다면 그만큼 Loss값이 줄어드는 것이죠.
그런데 어째서 W값에 비례한 값을 Loss에 더해주는 걸까요?
이를 직관적으로 한번 이해해 봅시다.
우리의 인공지능이 특정 데이터에만 치중되어 학습된다는 것은 무엇을 의미할까요?
지금까지 해 왔던 MNIST 데이터셋으로 예시를 들어 보겠습니다.
만약 우리가 숫자 "2"를 쓴 이미지를 인공지능에 넣었다고 합시다.
그러면, 인공지능은 이 이미지에서 2와 관련된 픽셀값의 특징을 확인해 가며, "2"에 해당하는 답으로 가중치를 바꿀 것입니다.
그런데 만약 우리가 지금 막 넣어준 "2"의 사진에, 어떤 특정 사람의 필체로 인해 아주 구석탱이가 검은 색으로 칠해져 있다고 생각해 봅시다.
그러면, 인공지능은 구석탱이에 칠해진 검은색 하나만을 보고도 이 사진이 2임을 추측할 수 있습니다.
이런 경우엔, 해당 구석탱이의 검은색에는 "2"라는 라벨이 붙는 가중치가 엄청 커지게 되고, 그 이후부터는 구석의 검은색만 보고도 그냥 "2"라고 해석하게 되는 것입니다.
이렇게 되어버리면, 당연히 문제가 발생하게 되겠죠.
이를 방지하기 위해, 특정 가중치 값이 너무 커지는 것을 방지하게 됩니다.
특히 L2의 경우, 전체적으로 가중치가 큰 것보다는 어떤 특정 가중치가 무식하게 커지는 것을 막는 것을 확인할 수 있습니다. (W^2에 비례하는 걸 보면 알 수 있습니다.)
L2 Regularization의 식은 간단합니다 - 간단하게는, $\lambda W^2$가 됩니다.
그리고, 이 값을 Loss값에 더해주면 됩니다.
설명은 이렇게 간단하게(?)만 하고, 코드를 봅시다.
class Model:
def __init__(self):
self.params = {}
self.grads = {}
self.keys = []
self.layers = {}
self.num = 0
self.l2 = {}
self.weight_decay_lambda = {}
self.loss = None
self.pred = None
def addlayer(self, layer, activation=False, input_size=None, name=None, initialization=None, reg=0):
if name is None:
name = str(self.num)
self.keys.append(name)
self.num += 1
self.layers[name] = layer
self.weight_decay_lambda[name] = reg
if not activation:
if isinstance(layer, AddLayer):
self.params[name] = np.zeros(input_size)
elif initialization is 'xavier':
self.params[name] = xavier_initialization(input_size)
elif initialization is 'he':
self.params[name] = he_initialization(input_size)
else:
self.params[name] = np.random.uniform(-1, 1, input_size)
self.layers[name].param = self.params[name]
def predict(self, x, y):
for i in range(len(self.keys) - 1):
key = self.keys[i]
x = self.layers[key].forward(x)
if key in self.l2:
self.l2[key] = np.sum(np.square(self.params[key])) * self.weight_decay_lambda[key]
self.loss = self.layers[self.keys[-1]].forward(x, y)
self.loss += sum(self.l2.values())/2
self.pred = softmax(x)이번엔 아예 Model Class 자체를 조금 바꿔야 합니다.
우선, L2 regularization 값들이 들어갈 self.l2를 선언해 주고 나서,
addlayer()에는 reg값을 추가했습니다. 이 reg값이 바로 위에서 언급했던 $\lambda$값입니다.
이 $\lambda$값들을 저장하는 변수 self.weight_decay_lambda도 추가해 주었습니다.
그 뒤, 마지막 predict에서 loss값에 l2의 값들의 합을 더해줍니다.
if key in model.params:
model.grads[key] = model.layers[key].grad + model.weight_decay_lambda[key] * model.params[key]
model.params[key] -= learning_rate * model.grads[key]optimizer.py의 SGD함수도 다음과 같이 바꿔줍시다.
비교해 보시면 아시겠지만, model.grads[key]의 update rule에 model.weight_decay_lambda와 관련된 식이 추가된 것을 볼 수 있습니다.
다음으로는 Dropout을 구현해 보겠습니다.
Dropout 또한 Overfitting을 막기 위해 고안된 녀석으로, 훈련 과정에서 뉴런들을 강제로 비활성화 시키며 학습을 진행합니다.
학습 시에는 조금 느리게 학습되나, overfitting을 매우 잘 막아줍니다.
바로 구현부로 넘어가 봅시다.
class Dropout:
def __init__(self, dropout_rate=0.2):
self.drop_rate = dropout_rate
self.mask = None
def forward(self, x, train_flag=True):
if train_flag:
self.mask = np.random.rand(*x.shape) > self.drop_rate
return x * self.mask
else:
return x * (1.0 - self.drop_rate)
def backward(self, dout):
return dout * self.maskDropout은 새로운 Layer로, Model 사이사이에 끼워 넣어 주며 뉴런을 버리게 만들 것입니다.
drop_rate는 버리는 정도를 의미하고, mask는 실제 버리는 index값들을 넣어줍니다.
그리고, 이 Dropout은 훈련 중에는 계속 뉴런을 조금씩 버리면서 학습하지만, 훈련 중이 아닐 때는 (즉, test때는) 뉴런을 버리는 대신 drop_rate만큼 줄여서 모든 뉴런을 내보냅니다.
또, 역전파 시에는 forward때 보내줬던 만큼의 뉴런만을 받아서 뒤로 보냅니다.
def predict(self, x, y, train_flag=True):
for i in range(len(self.keys) - 1):
key = self.keys[i]
if isinstance(self.layers[key], Dropout):
x = self.layers[key].forward(x, train_flag)
else:
x = self.layers[key].forward(x)
if key in self.l2:
self.l2[key] = np.sum(np.square(self.params[key])) * self.weight_decay_lambda[key]Model.py의 predict 함수도 위와 같이 수정해 줍시다.
이렇게 수정하게 되면, predict 시에 train_flag를 설정하여 dropout을 발동시킬지, 발동시키지 않을지 결정할 수 있습니다.
model.predict(x_train, y_train, train_flag=False)
print("Final train_ACC : ", (model.pred.argmax(1) == y_train.argmax(1)).mean())
print("Final train_LOSS : ", model.loss)Optimizer.py의 함수들에는 위와 같이, 최종 test 시에는 train_flag를 False로 바꾸어서 나오게 해야 합니다.
import numpy as np
import pandas as pd
from Model import Model
import Layers
import Optimizer
# load data
train = pd.read_csv("../Data/MNIST_data/mnist_train.csv")
y_train = train["label"]
x_train = train.drop("label", 1)
x_train = x_train.values / x_train.values.max()
y_train = y_train.values
# y to one-hot
one_hot = np.zeros((y_train.shape[0], y_train.max() + 1))
one_hot[np.arange(y_train.shape[0]), y_train] = 1
y_train = one_hot[:300]
y_test = one_hot[300:600]
x_test = x_train[300:600]
x_train = x_train[:300]
# initialize parameters
num_classes = y_train.shape[1]
hidden = 50
model = Model()
model.addlayer(Layers.MulLayer(), input_size=(784, 100), name="w1", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=100, name='b1')
model.addlayer(Layers.ReLU(), activation=True, name='relu1')
model.addlayer(Layers.Dropout(), activation=True, name='dropout1')
model.addlayer(Layers.MulLayer(), input_size=(100, 100), name="w2", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=100, name='b2')
model.addlayer(Layers.ReLU(), activation=True, name='relu2')
model.addlayer(Layers.Dropout(), activation=True, name='dropout2')
model.addlayer(Layers.MulLayer(), input_size=(100, 100), name="w3", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=100, name='b3')
model.addlayer(Layers.ReLU(), activation=True, name='relu3')
model.addlayer(Layers.Dropout(), activation=True, name='dropout3')
model.addlayer(Layers.MulLayer(), input_size=(100, 100), name="w4", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=100, name='b4')
model.addlayer(Layers.ReLU(), activation=True, name='relu4')
model.addlayer(Layers.Dropout(), activation=True, name='dropout4')
model.addlayer(Layers.MulLayer(), input_size=(100, 100), name="w5", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=100, name='b5')
model.addlayer(Layers.ReLU(), activation=True, name='relu5')
model.addlayer(Layers.Dropout(), activation=True, name='dropout5')
model.addlayer(Layers.MulLayer(), input_size=(100, 10), name="w6", initialization='he', reg=0.01)
model.addlayer(Layers.AddLayer(), input_size=10, name='b6')
model.addlayer(Layers.Dropout(), activation=True, name='dropout6')
model.addlayer(Layers.SoftmaxLayer(), activation=True, name='softmax')
optimizer = Optimizer.SGD(batch_size=128)
model.train(x_train, y_train, optimizer, 3000, 0.01)
model.predict(x_test, y_test, train_flag=False)
print("Final test_ACC : ", (model.pred.argmax(1) == y_test.argmax(1)).mean())
print("Final test_LOSS : ", model.loss)
최종적으로, 다음의 코드를 돌려보시기 바랍니다.
overfitting을 유도하기 위해 데이터를 300개 가량으로 줄였고, model의 크기는 늘렸습니다.
reg값을 바꿔도 보고, Dropout rate를 바꿔도 보고 하며 어떤 값들이 가장 overfitting을 줄이는지 확인할 수 있을 겁니다.
여기까지 기본적인 딥러닝 코드가 끝났습니다!
다음 시간부터는 CNN을 직접 구현해 보는 시간을 가지도록 하겠습니다!
'인공지능 > 딥러닝 직접 구현하기 프로젝트' 카테고리의 다른 글
| 딥러닝 직접 구현하기 프로젝트 3-1차시: Convolution Layer 틀 잡기 (0) | 2020.08.11 |
|---|---|
| 딥러닝 직접 구현하기 프로젝트 2-7차시 - 코드 정리 + Model Save / Load (0) | 2020.08.01 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Gradient Descent Optimizer 구현하기 (2) (2) | 2020.07.07 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Optimizer (Momentum, NAG) 구현하기 (1) (4) | 2020.06.30 |
| 딥러닝 직접 구현하기 프로젝트 2-4차시 - Model 제작하기 (0) | 2020.06.23 |
딥러닝 직접 구현하기 프로젝트 2-5차시 - Gradient Descent Optimizer 구현하기 (2)
* 모든 코드는 제 깃허브 (cdjs1432/DeepLearningBasic: Deep Learning from scratch)에서 확인할 수 있습니다.
* 시작하기에 앞서, 해당 포스트는 "Gradient Descent Optimization Algorithms 정리" 포스팅
(http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html)
을 참조하였습니다. 구현 중인 알고리즘에 대해 알고 싶다면, 위 포스팅에서 확인해 주세요.
또한, 이번 차시에 구현할 optimizer는 위 링크의 Ada시리즈와 RMSProp을 구현할 것입니다.
자, 저번 시간에 이어, 이번에는 바로 Adagrad를 구현해 봅시다.
우선 AdaGrad의 식은 다음과 같습니다.
$$ G_t = G_{t-1} + (\nabla_\theta J(\theta_t))^2 $$
$$ \theta_{t+1} = \theta_t - \frac {\eta} {\sqrt{G_t + \epsilon}} \cdot \nabla_\theta J(\theta_t) $$
여기서, $\epsilon$은 분모가 0이 되는 것을 방지하기 위한 값입니다.
간단하게만 설명하자면, $G_t$는 저번의 velocity와 같이, params(또는 grads)만큼의 크기를 갖는 새로운 변수입니다.
학습하면 할수록, 계속해서 grads의 제곱의 합을 받아오는 변수입니다.
이 변수는 해당 grads의 절대값이 크면 G의 값을 크게, grads의 절대값이 작으면 G의 값을 작게 둡니다.
그리고 update rule에서 보면 알겠지만 G의 값이 크면 learning rate가 작고, G의 값이 작으면 learning rate가 큽니다.
우리의 변수 params들은 grads의 값이 크면 많이 움직이고, 값이 작으면 조금 움직이게 됩니다.
그러므로, 위의 G가 가지는 의미는 "이미 많이 움직인 params는 좀 덜 움직이고, 많이 안 움직였던 params은 더 크게 움직이자" 하는 뜻입니다.
저번의 NAG처럼 복잡하게 수식을 정리할 필요는 없으니, 빠르게 구현해 봅시다.
class Adagrad:
def __init__(self, batch_size):
self.x = None
self.y = None
self.model = None
self.batch_size = batch_size
self.epsilon = 10e-8
def train(self, x_train, y_train, epoch, learning_rate, model):
G = {}
for p in model.params:
G[p] = np.zeros(model.params[p].shape)
for epochs in range(epoch):
batch_mask = np.random.choice(x_train.shape[0], self.batch_size)
x = x_train[batch_mask]
y = y_train[batch_mask]
model.predict(x, y)
dout = model.layers[model.keys[-1]].backward()
for i in reversed(range(len(model.keys) - 1)):
key = model.keys[i]
dout = model.layers[key].backward(dout)
if key in model.params:
model.grads[key] = model.layers[key].grad
G[key] += np.square(model.grads[key])
model.params[key] -= np.multiply(learning_rate / (np.sqrt(G[key] + self.epsilon)), model.grads[key])
if epochs % (epoch / 10) == 0:
print("ACC on epoch %d : " % epochs, (model.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS on epoch %d : " % epochs, model.loss)
model.predict(x_train, y_train)
print("Final train_ACC : ", (model.pred.argmax(1) == y_train.argmax(1)).mean())
print("Final train_LOSS : ", model.loss)
(아무래도 코드가 많이 중복되는 것을 보아하니, 코드를 다시 한번 리팩토링을 언젠가 해야겠습니다.)
이번에 볼 부분은, 다음과 같습니다.
1. __init__의 epsilon 등장
2. 변수 G의 등장
3. Update Rule의 적용
이 때, 변수 G는 저번 Momentum / NAG 때와 동일하게 선언해 주시면 됩니다. (결국 변수의 크기 자체는 동일하기 때문)
그리고, 식을 그대로 코드에 적용시켰습니다.
model.grads[key] = model.layers[key].grad
G[key] += np.square(model.grads[key])
model.params[key] -= np.multiply(learning_rate / (np.sqrt(G[key] + self.epsilon)), model.grads[key])update의 식은 다음과 같습니다.
G에는 grads의 제곱을 계속해서 더해주고, params에는 위 계산식 그대로 넣어주시면 되겠습니다.
하지만, Adagrad에는 큰 단점이 있는데, 아무리 학습이 안되었어도 / 잘되었어도 가면 갈수록 계속해서 learning rate가 작아집니다.
G에는 계속해서 grad의 제곱이 더해지므로, 가면 갈수록 점점 더 G가 커지기 때문입니다.
이를 보완한 알고리즘 중 하나가 바로 RMSProp입니다.
RMSProp의 식은 다음과 같습니다.
$$ G_t = \gamma G_{t-1} + (1-\gamma)(\nabla_\theta J(\theta_t))^2 $$
$$ \theta_{t+1} = \theta_t - \frac {\eta} {\sqrt{G_t + \epsilon}} \cdot \nabla_\theta J(\theta_t) $$
여기서 gamma는 보통 0.9, 0.99 등의 값으로 많이 놓습니다.
또한, update rule은 동일함을 알 수 있습니다.
이렇게 구현하게 되면, gamma로 인해 G값이 무한으로 뻗어나가는 일은 생기지 않게 됩니다.
식에 큰 변화가 없으니, 그냥 간단하게 짜봅시다.
class RMSProp:
def __init__(self, batch_size, gamma=0.9):
self.x = None
self.y = None
self.model = None
self.batch_size = batch_size
self.epsilon = 10e-8
self.gamma = gamma
def train(self, x_train, y_train, epoch, learning_rate, model):
G = {}
for p in model.params:
G[p] = np.zeros(model.params[p].shape)
for epochs in range(epoch):
batch_mask = np.random.choice(x_train.shape[0], self.batch_size)
x = x_train[batch_mask]
y = y_train[batch_mask]
model.predict(x, y)
dout = model.layers[model.keys[-1]].backward()
for i in reversed(range(len(model.keys) - 1)):
key = model.keys[i]
dout = model.layers[key].backward(dout)
if key in model.params:
model.grads[key] = model.layers[key].grad
G[key] = self.gamma * G[key] + (1 - self.gamma) * np.square(model.grads[key])
model.params[key] -= np.multiply(learning_rate / (np.sqrt(G[key] + self.epsilon)), model.grads[key])
if epochs % (epoch / 10) == 0:
print("ACC on epoch %d : " % epochs, (model.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS on epoch %d : " % epochs, model.loss)
model.predict(x_train, y_train)
print("Final train_ACC : ", (model.pred.argmax(1) == y_train.argmax(1)).mean())
print("Final train_LOSS : ", model.loss)
__init__ 부분에 gamma가 생겼다는 것, 그리고 식에 gamma와 관련된 식이 생겼다는 것을 제외하고는 모두 그대로입니다.
다음은 AdaDelta입니다.
AdaDelta는 위의 두 알고리즘과는 달리 식 4개로 이루어져 있습니다.
$$ G = \gamma G + (1 - \gamma ) (\nabla_\theta J(\theta))^2 $$
$$ \Delta_\theta = \frac{\sqrt{s+\epsilon}}{\sqrt{G+\epsilon}} \cdot \nabla_\theta J(\theta)$$
$$ \theta = \theta - \Delta_\theta $$
$$ s = \gamma s + (1 - \gamma) \Delta^2 _\theta $$
식을 딱 보았을 때의 첫느낌은 아마, "대체 뭐라는거지?" 일 것 같습니다.
일단 G의 식은 지금까지와 같으나, $\theta$를 update하는 과정에서 분자에 learning rate $\eta$가 들어가는 것이 아니라, 새로운 인자 $\sqrt{s+\epsilon}$이 들어갑니다.
또한 눈치챌 수 있는 점은, learning rate는 AdaDelta에서는 사용하지 않습니다.
즉, 따로 learning rate를 설정해 주지 않아도 작동을 한다는 뜻입니다.
대충 정리하자면, learning rate를 변수 $\sqrt{s+\epsilon} = \sqrt{\gamma s + (1 - \gamma) \Delta^2 _\theta + \epsilon}$ 가 대체한다는 것입니다.
$\Delta_\theta^2 = \frac{s+\epsilon}{G+\epsilon} \cdot (\nabla_\theta J(\theta))^2$ 이므로, s에 관한 식을 다시 풀어 쓴다면 $s = \gamma s + (1 - \gamma)(\frac{s+\epsilon}{G+\epsilon} \cdot (\nabla_\theta J(\theta))^2)$가 되겠습니다.
이것을 보면, G와 s가 매우 비슷한 방식으로 update된다는 것을 알 수 있습니다.
그리고, G와 s를 간단하게나마 설명하자면, G는 "지금까지 grads의 변화의 합", s는 "지금까지의 params의 변화의 합"이 됩니다.
즉, params가 크게 변화하면 learning rate (즉, $\sqrt{s+\epsilon}$값)이 커지고, params가 작게 변화하면 learning rate가 작아지는 것입니다.
이를 직관적으로 보자면, local minima에 갇혀 있다가 풀려난 경우에는 갑자기 params가 변화해야 하는 정도가 커지는데, 그렇게 된다면 자동으로 learning rate를 증가시켜 더욱 빠르게 (또, 관성을 갖게) 됩니다.
그리고, global minima에 가까워지면 저절로 params의 변화 정도가 적어지므로, learning rate를 감소시켜 더욱 세밀한 update가 가능해 지는 것입니다.
코드는 이번에도 크게 바뀌진 않습니다.
class AdaDelta:
def __init__(self, batch_size, gamma=0.9):
self.x = None
self.y = None
self.model = None
self.batch_size = batch_size
self.epsilon = 10e-8
self.gamma = gamma
def train(self, x_train, y_train, epoch, learning_rate, model):
G = {}
s = {}
for p in model.params:
G[p] = np.zeros(model.params[p].shape)
s[p] = np.zeros(model.params[p].shape)
for epochs in range(epoch):
batch_mask = np.random.choice(x_train.shape[0], self.batch_size)
x = x_train[batch_mask]
y = y_train[batch_mask]
model.predict(x, y)
dout = model.layers[model.keys[-1]].backward()
for i in reversed(range(len(model.keys) - 1)):
key = model.keys[i]
dout = model.layers[key].backward(dout)
if key in model.params:
model.grads[key] = model.layers[key].grad
G[key] = self.gamma * G[key] + (1 - self.gamma) * np.square(model.grads[key])
d_t = np.multiply(np.sqrt(s[key] + self.epsilon) / np.sqrt(G[key] + self.epsilon), model.grads[key])
s[key] = self.gamma * s[key] + (1 - self.gamma) * np.square(d_t)
model.params[key] -= d_t
if epochs % (epoch / 10) == 0:
print("ACC on epoch %d : " % epochs, (model.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS on epoch %d : " % epochs, model.loss)
model.predict(x_train, y_train)
print("Final train_ACC : ", (model.pred.argmax(1) == y_train.argmax(1)).mean())
print("Final train_LOSS : ", model.loss)
__init__은 동일하고,
train 함수에서 s변수를 새로 만들어서 s값을 저장하게 합니다.
그리고, 계산 식은 위에서 쓴 식과 동일하게 적용했습니다.
(d_t는 $\Delta_\theta$를 줄여 쓴 것입니다.)
마지막으로, Adam에 대해 설명하겠습니다.
Adam은 RMSProp와 Momentum을 섞은 듯한 알고리즘입니다.
식으로 먼저 볼까요?
$$ m_t = \beta _1m_{t-1} + (1-\beta _1)\nabla_\theta J(\theta) $$
$$ v_t = \beta _2v_{t-1} + (1-\beta _2)(\nabla_\theta J(\theta))^2 $$
여기서 $\beta_1, \beta_2$는 위의 $\gamma$와 동일한 역할을 합니다.
그러면... 지금까지 RMSProp과 Momentum만 제대로 이해하셨다면 어떤 느낌인지 아실 겁니다!
이제 이것들을 사용해서 $\theta$를 update를 할 텐데, 왜 $\theta$의 update 식을 안썼을까요?
잘 생각해 보시면 알겠지만, m와 v값은 처음에 0으로 초기화 될 겁니다.
그런데, 위 식을 그대로 따라간다면, m값과 v값은 초기에 0에 매우 가깝게 다가가므로, 이 값들이 편향성을 갖게 됩니다.
그래서 위 식을 그대로 가져다 쓰지 않고, 다음과 같은 식을 사용합니다.
$$ \hat{m_t} = \frac{m_t}{1-\beta_1^t}$$
$$ \hat{v_t} = \frac{v_t}{1-\beta_2^t} $$
$$ \theta = \theta - \frac{\eta}{\sqrt{\hat{v_t}+\epsilon}}\hat{m_t} $$
그리고, 보통 $\beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}$를 사용합니다.
자, 이제 이를 토대로 코드를 구현해 봅시다!
class Adam:
def __init__(self, batch_size, beta_1 = 0.9, beta_2 = 0.999):
self.x = None
self.y = None
self.model = None
self.batch_size = batch_size
self.epsilon = 10e-8
self.beta_1 = beta_1
self.beta_2 = beta_2
def train(self, x_train, y_train, epoch, learning_rate, model):
m = {}
m_hat = {}
v = {}
v_hat = {}
for p in model.params:
m[p] = np.zeros(model.params[p].shape)
m_hat[p] = np.zeros(model.params[p].shape)
v[p] = np.zeros(model.params[p].shape)
v_hat[p] = np.zeros(model.params[p].shape)
for epochs in range(epoch):
batch_mask = np.random.choice(x_train.shape[0], self.batch_size)
x = x_train[batch_mask]
y = y_train[batch_mask]
model.predict(x, y)
dout = model.layers[model.keys[-1]].backward()
for i in reversed(range(len(model.keys) - 1)):
key = model.keys[i]
dout = model.layers[key].backward(dout)
if key in model.params:
model.grads[key] = model.layers[key].grad
m[key] = self.beta_1 * m[key] + (1 - self.beta_1)*model.grads[key]
m_hat[key] = m[key] / (1 - self.beta_1 * self.beta_1)
v[key] = self.beta_2 * v[key] + (1 - self.beta_2) * model.grads[key] * model.grads[key]
v_hat[key] = v[key] / (1 - self.beta_2 * self.beta_2)
model.params[key] -= learning_rate * m_hat[key] / np.sqrt(v_hat[key] + self.epsilon)
if epochs % (epoch / 10) == 0:
print("ACC on epoch %d : " % epochs, (model.pred.argmax(1) == y.argmax(1)).mean())
print("LOSS on epoch %d : " % epochs, model.loss)
model.predict(x_train, y_train)
print("Final train_ACC : ", (model.pred.argmax(1) == y_train.argmax(1)).mean())
print("Final train_LOSS : ", model.loss)사실 여기도 위 식을 그냥 그대로 갖다 박은거 밖에 없어서 설명할 게 딱히 없습니다.
다음 시간에는, Regularization을 비롯한 다양한 테크닉들을 적용해 보도록 하겠습니다!
'인공지능 > 딥러닝 직접 구현하기 프로젝트' 카테고리의 다른 글
| 딥러닝 직접 구현하기 프로젝트 2-7차시 - 코드 정리 + Model Save / Load (0) | 2020.08.01 |
|---|---|
| 딥러닝 직접 구현하기 프로젝트 2-6차시 - 가중치 초기화, 정규화, 드롭아웃 (0) | 2020.07.29 |
| 딥러닝 직접 구현하기 프로젝트 2-5차시 - Optimizer (Momentum, NAG) 구현하기 (1) (4) | 2020.06.30 |
| 딥러닝 직접 구현하기 프로젝트 2-4차시 - Model 제작하기 (0) | 2020.06.23 |
| 딥러닝 직접 구현하기 프로젝트 2-3차시 - Activation Function (활성화 함수) 구현하기 (2) | 2020.06.17 |