분류 전체보기
-
CS234 Assignment 2-4 solution 및 풀이2019.06.07
-
CS234 Assignment 2-3 solution 및 풀이2019.06.07
-
CS234 Assignment 2-2 solution 및 풀이2019.06.07
-
CS234 Assignment 2-1 solution 및 풀이2019.05.29
-
CS234 Assignment 1-4 solution 및 풀이 (코드)2019.05.29
-
CS234 Assignments 1-2 Solution 및 풀이2019.05.28
(번외편) 자연어 처리 - 텍스트 분류 & 문장 representation
https://www.edwith.org/deepnlp/joinLectures/17363
딥러닝을 이용한 자연어 처리 강좌소개 : edwith
- 조경현 교수
www.edwith.org
edwith 조경현 교수님의 자연어 처리 강좌 중, C. Text Classification & Sentence Representation 부분을 정리한 글입니다.
사실 학교 보고서로 제출한 내용인데 그냥 그대로 놓고 있긴 좀 아까워서...ㅎㅎ
1. 텍스트 분류란?
텍스트 분류란, 단어, 문장 또는 지문 전체를 두고 카테고리 별로 구분하는 것을 의미합니다. 이미지 분류 문제와 비슷하게 지도 학습 (supervised learning)으로 작업을 하게 됩니다.
텍스트 분류에는 다양한 종류가 있습니다.
1. 감성 분석
말 그대로, 문장 또는 지문의 감성을 분석하는 것입니다.
대표적인 예시로, 영화 리뷰를 보고 긍정적인 리뷰인지 부정적인 리뷰인지 분석하는 것이 있습니다.
가령 “이 영화는 역대 최악의 영화이다” 라는 문장을 분석한다면, “부정적”인 리뷰로 분류하는 것이 맞겠지요.
2. 카테고리 분류
이것도 말 그대로 문장이나 지문을 카테고리 별로 분류하는 것입니다.
어떤 블로그의 글을 보고 그 글이 IT관련 글인지, 스포츠 관련 글인지 등등을 분류하는 것도 이 카테고리 분류로 볼 수 있겠고, 나에게 온 메일이 스팸 메일인지 그냥 메일인지 분류하는 것도 카테고리 분류로 볼 수 있겠습니다.
3. 의도 분류
이것도 또 말 그대로 문장의 의도를 분류하는 것입니다.
가령 챗봇한테 “오늘 주말에 영업하는 안산 중앙동에 있는 식당 추천해 줘” 라고 말을 했을 때, 챗봇한테 이 말이 어떤 의도를 갖고 한 말인지 분류하게 하는 것입니다. 위의 경우에는 “식당 추천”이 의도가 될 것이고, 그러면 챗봇은 그 의도 안에서 “오늘 주말에 영업”, “안산 중앙동에 있는” 이라는 두 구문을 알아서 잘 해석해서 답을 알려 줄 것입니다.
2. 문장과 토큰
문장을 그냥 그대로 곧이곧대로 자연어 처리 모델에 적용하는 것은 사실상 불가능합니다.
그렇기 때문에 문장을 자연어 처리 모델에 적용시킬 때는, 문장을 “토큰”이라는 단위로 나눕니다.
이 때, 토큰은 매우 추상적이고, 임의적인 성질을 지닙니다.
예를 들자면, 분명 늑대와 개는 비슷한 성질을 가졌지만 말은 아예 다르고, “수학”과 “수화”는 매우 다른 의미를 가졌지만 말은 굉장히 비슷합니다.
문장을 토큰으로 나누는 방식은 굉장히 다양합니다.
“자연어 처리를 공부하는 중입니다.” 라는 문장만 보더라도,
· 자연어, 처리를, 공부하는, 중입니다 (띄어쓰기로 나누기),
· 자연어, 처리, 를, 공부, 하는, 중, 입니다 (형태소로 나누기),
· 자, 연, 어, (공백), 처, 리, 를, (공백), 공, 부, 하, 는, (공백), 중, 입, 니, 다 (어절마다 나누기)
등등이 있습니다.
또, 이렇게 나눈 토큰들을 컴퓨터에게 주려면 이 토큰들을 숫자로 변환해 주어야 합니다.
이미지를 컴퓨터에 입력할 때 픽셀 값으로 입력하는 것과 비슷한 맥락입니다.
이 토큰들을 숫자로 변환해 주기 위해, 이 토큰들로 Vocabulary(단어장)을 만들어서 인덱스 값을 토큰들에 부여합니다.
가령 위 예시에서 형태소로 나누었다고 했을 때, Vocabulary가 (자연어, 처리, 를, 공부, 하는, 중, 입니다) 로 나누어져 있다면 “자연어” 는 0, “공부”는 3, “입니다”는 6이 될 것입니다.
하지만, 우리들은 비슷한 의미를 가진 토큰은 가깝게, 다른 의미를 가진 토큰은 멀리 배치하고 싶습니다. 그런 점에서 위처럼 저렇게 막 배열하는 것은 큰 의미가 없습니다.
이렇게 비슷한 의미를 가진 토큰은 가까이, 다른 의미를 가진 토큰은 멀리 배치하기 위해서 실행할 수 있는 것이 One-hot Encoding입니다.
One-hot Encoding이란, 길이가 단어장(V)인 벡터에서, 단어의 인덱스 위치에 있는 값만 1, 나머지는 모두 0으로 두는 형식입니다.
가령 위 예시에서 “공부”를 One-hot Encoding 하게 되면
[0, 0, 0, 1, 0, 0, 0]으로 인코딩 될 것입니다.
그러나 그냥 이렇게 인코딩만 한다고 해서 단어의 유사성이 거리에 영향을 미치게 되진 않습니다. (One-hot Encoding을 하면 모든 토큰들의 거리가 동일해 집니다.)
이를 해결하기 위해, Embedding이라는 과정을 거치게 됩니다.
Embedding이란, 각 토큰을 일종의 테이블에 집어넣는 방식입니다. 이를 하기 위해서, 인공 신경망의 Weight W에다가 One-hot Encoding된 각 토큰을 내적하게 됩니다. 이렇게 하면, 모든 토큰들은 이제 더 큰 차원의 연속적인 벡터로 변환되게 됩니다. 이렇게 변환된 토큰들은 이제 각각의 토큰의 거리가 달라지기 때문에, 여기서 의미의 유사성을 찾을 수 있게 됩니다.
3. 문장을 표현하는 방법들 (CBoW, RN, CNN, Self Attention, RNN)
이제 Vocabulary에 있는 토큰을 처리하는 것은 끝났습니다.
하지만, 이것 만으로는 충분하지 않습니다. 우리는 문장을 input값으로 집어넣는 것이지, 각각의 토큰을 input 값으로 넣어주는 것이 아니기 때문입니다.
하지만 각각의 문장은 모두 길이가 다릅니다. 엄청나게 긴 문장이 있는가 하면, 엄청나게 짧은 문장도 있기 마련입니다. 이 길이가 다른 문장들을 그대로 모델에 집어넣는 것은 사실상 불가능합니다. 그렇기 때문에, 이 문장을 나타내는 방법이 중요하게 됩니다. 각 토큰을 나타낸 것 같이 말입니다.
이 때 사용하는 방법 중 CBow, RN, CNN, Self Attention, RNN 방식을 알아봅시다.
· CBoW (Continuous Bag of Words)
CBow는 그냥 문장에 담겨 있는 토큰의 평균값을 내는 매우 간단한 방식으로 문장을 나타냅니다. 이게 뭔 이상한 짓인가 생각이 들기도 하지만, 충격적이게도 이 방식은 굉장히 성능이 좋다고 합니다. 연산 속도도 매우 빠르고, 성능도 괜찮기 때문에 어떤 자연어 처리 문제를 만나도 일반적인 baseline 역할을 해 준다고 합니다.
· RN (Relation Network)
Relation Network는 말 그대로, 단어들 사이의 관계를 보는데, 문장 안의 모든 토큰 쌍을 보고, 각 쌍에 대한 신경망을 만드는 방식으로 이루어 집니다.
가령 인덱스 값으로 본다면, (1, 2), (1, 3), …, (1, n), (2, 3), (2, 4), …. 같이 쌍을 지어 준 뒤에, 각 쌍에 대한 신경망을 만들어서 (W 곱하고 b 더하고…) 그 값들을 전부 다 평균을 내 줍니다.
물론 두 단어를 묶는 게 아니라 세 단어, 네 단어, … 끼리 묶을 수도 있지만, 이렇게 묶는 단어의 수가 늘어나면 늘어날수록 연산 횟수가 기하급수적으로 늘어나게 됩니다. (효율성이 떨어지게 됩니다.)
이 방식을 채용하면 단어들 사이의 연관성을 파악하면서 문장을 표현할 수 있다는 장점이 있지만, 아예 관계없는 단어 쌍도 같이 계산한다는 단점이 존재합니다.
· CNN (Convolutional Neural Network)
이미지 처리에서 쓰던 CNN을 그대로 1차원 형식으로 가져와서 문장에 적용합니다.
문장 안에서 CNN을 사용해서 층을 쌓고, 그 층(layer)에서 다시 CNN을 사용해서 layer을 중첩하는 방식으로 진행됩니다.
이렇게 하면, 점층적으로 더 넓은 범위의 토큰들 사이의 관계를 파악할 수 있습니다.
필터의 크기가 3이었다고 한다면, 첫번째 layer에서는 주변 3개의 단어와의 관계를 파악하고, 두 번째 layer에서는 주변 5개의 단어와의 관계를 파악하고… 하는 식입니다.
이렇게 문장을 보면, 단어 -> 다중 단어 표현 -> 구문 -> 문장 순으로 문장을 분석하는 인간의 인식과도 알맞게 됩니다.
· Self Attention
위에서 언급했던 RN과 CNN을 다시 봅시다.
RN에서 t번째 토큰의 표현은 f(xt,x1) + f(xt, x2) + f(xt , x3) + … + f(xt, xT)로 볼 수 있고,
CNN에서 t번째 토큰의 표현은 f(xt, xt-k) + … + f(xt,xt) + … + f(xt, xt+k)로 볼 수 있습니다.
그런데, CNN은 가중치를 xt근처 k개를 1, 나머지를 0이라고 둔 RN이라고 볼 수도 있게 됩니다.
그런데, 이렇게 가중치를 1 또는 0으로 두는 것이 아니고 0에서 1 사이의 값으로 둘 수 있을 것 같습니다.
RN에다가 가중치를 1 또는 0을 두어서 CNN 연산을 할 것이 아니라, 토큰마다의 연관성을 찾는 function을 두어서 그 function값을 가중치로 둘 수도 있는데, 이를 Self Attention 방식이라고 합니다. (이 function은 또 다른 인공 신경망으로 구할 수 있습니다.)
이러면 이제 RN처럼 단어들마다 가중치를 곱해줘서 연관성이 없는 단어들은 가중치를 0에 가깝게 두고, 연관성이 있는 단어들은 가중치를 1에 가깝게 둬서 연관성이 높은 토큰을 강조하고, 연관성이 낮은 토큰을 억제할 수 있습니다.
또한, 먼 거리에서도 연관성이 높은 단어들을 가져올 수 있고, 짧은 거리에서도 마찬가지로 가능하니 거리에 큰 영향을 받지 않게 됩니다.
하지만, 계산 복잡도가 굉장히 높다는 단점이 있습니다.
· RNN (Recurrent Neural Network)
다른 방식으로는 RNN이 있습니다. 이 방식은 단어 처음과 끝 모두의 쌍을 맺어주며 나아가는 Self Attention 방식과는 달리 그냥 문장을 처음부터 쭉 읽어가면서, 매번 토큰 하나씩을 읽을 때 마다 메모리에 토큰을 저장해 가면서 나아갑니다. 토큰들을 메모리에 압축시키는 형식인 것입니다. 그렇게 마지막에 나온 메모리 벡터를 갖고 문장을 표현하게 됩니다.
단점으로, 토큰을 하나하나 읽어야 하는 특성 상 연산 속도가 다른 것들보다 느리게 되고, 순차적으로 읽는다는 점 때문에 나아가면 나아갈수록 예전에 읽어왔던 메모리를 잊게 되어 정보의 손실이 일어납니다. 이 점들은 나중에 나온 LSTM, GRU와 같은 RNN의 변형이 나오면서 어느 정도 해결됩니다.
이렇게 자연어 처리의 기본적인 부분만 가볍게(?) 살펴 보았습니다.
앞으로 시간이 더 난다면 조금 더 깊게, 조금 더 많은 내용을 살펴보고 싶습니다만,
공업 일반 1인 1프로젝트로 다시 강화 학습을 공부할 예정이라 시간이 날지 모르겠습니다.
디미고 시험기간 - 최대 헬게이트, 고2 1학기 기말

디미고는 유독 정시 비율이 다른 학교들보다 높은 학교이다. 대략 정시 70% / 수시 30% 비율 정도로 이루어져 있다.
아무래도 아이들 수준이 조금 높아서 정시도 어느 정도 잘 보고, 사람 수도 적어서 내신 등급을 따기 힘든 탓일 것이다.
하지만, 연세대/고려대는 특성화고 전형이 수시(였)고, 상위권 대학에서는 한양대 / 중앙대 / 세종대 등 일부만 제외하면 모두 특성화고 전형이 수시이기 때문에 일반적으로 "수시 준비를 한다" = "좋은 상위권 대학을 노린다" 정도로 보여진다.
그리고 고1 시절, 1학년 1학기 내신을 터뜨리고 2학기때 수습하느라 고생한 나는 '이렇게만 계속 공부하면 수시로 가겠는데?' 하는 생각을 갖고 있었다.
연세대, 고려대 정도는 사실 딱히 바라지도 않았고 (1학기때 너무 터뜨렷다.. ㅠㅠ)
상향지원 넣으면 성균관대정도는 넣을 수 있지 않을까? 아니 그냥 시립대에 지원해도 붙을수나 있을까? 하는 생각의 반복과 함께, 나는 2학년에 접어들었다.
2학년 시험기간이 얼마나 헬인지 미처 알기도 전에...
2학년 시험기간, 그러니까, 지금, 나는 왜 사람들이 수시를 때려친다는 이야기를 하는지 이해가 된다.
여러 가지 이유가 복합적으로 섞여서 학생들이 공부를 놔버리는 일이 생기는 것이다.
그 이유들에 대해서 이야기해 보려고 한다.
첫 번째 이유로는, 과목이 1학년때보다 조금 많다는 것이 있다.
1학년때는 국어 / 영어 / 수학 / 사회 / 과학 / 한국사 / 프로그래밍 / 컴퓨터 일반 총 8과목인데,
2학년때는 문학 / 영어 / 수학 / 공업수학 / 화학1 / 중국어 / 자료구조 (자바) / 공업일반 / 정보통신 / 기초제도로 총 10과목이다.
선택형 강좌를 더 수강하는 사람들은, (빅데이터 분석 / 정보과학) 과목이 하나 더 늘어난다.
그럼 늘어봤자 2~3개 느는거 아니냐고 할 수 잇겠지만, 비율로 따지면 공부량이 약 25%나 늘어난 것이다.
근데 거기다가 중국어랑 기초 제도는 절대평가 과목도 아니고 상대평가 과목이다.
그러니까, 다른 아이들과 경쟁해야 하는 과목 (= 선생님들이 변별력 있게 문제를 출제하는 과목)이 1학년때와 같이 6개에다가, 외우는 양 많은 절대평가들까지 추가된다.
이렇게 많은 과목 수는 중간고사 때의 과목 수와 대조되면서 더 큰 효과를 불러일으킨다. (문학 개념 ㅎ)
중간고사 때는 공부할 시간도 많았는데 5과목밖에 안되는 (상대평가는 4과목밖에 안되는) 과목들을 공부하다가
갑자기 10과목을 공부하려니 정신이 없다.
(물론 중간고사 공부가 쉽다는 이야기가 아니다. 5과목밖에 안된지라 아이들이 그만큼 또 공부를 많이 해서 하나만 틀려도 무슨 15등이나 밀리는 시험들이 되어버렸다...)
두 번째 이유는 바로 수학여행 + 수행평가 연타이다.
중간고사를 끝내고 어느 정도 수업을 더 진행한 뒤에 수학여행을 다녀오는데, 이게 정말 치명적으로 작용한다.
다들 알다시피, 수학여행 끝나고 얼마정도는 진짜 그냥 정신줄을 놓고 살게 된다.
그리고 그 다음주에 (다다음주였나...) 현충일로 수요귀가 (진짜 흔치 않다!)를 하게 되니까, 더 정신을 차리기 힘들어진다.
그런데 그러고 학교에 돌아오면? 시험이 한 달이 남아있다.
아직 정신을 차리기도 전인데, 시험이 한 달 남았다는 사실은 큰 충격으로 다가왔다.
그런데, 문제가 하나 더 있다.
선생님들이 아이들 배려해 주신다고, 수학여행 전후에는 수행평가를 그렇게 많이 두지 않는다.
그러면 10~11개의 과목의 수행평가는 다 어디에 배치될까??
시험이 한 달 정도 남았을 무렵 일주일에 수행평가가 한두개씩 스멀스멀 올라오다가,
시험 2주 전 한 주 동안 마감해야 할 수행평가가 무려 7~8개정도나 됐다.
그것들이 또 쉬우면 모르는데, 자바 프로젝트 진행 (사실 이건 쌤이 기간을 한 달 준거긴 하지만 ㅎㅎ..), 국어 UCC 같은 대형 프로젝트들이 끼어있는 터라 아이들이 분주해질 수 밖에 없다.
그리고, 솔직히 수행평가를 7~8개를 한 주만에 마감을 다 하면, 어떻게 모든 아이들이 다 행복하게 점수를 받겠는가?
누구는 수학 수행 준비하느라 중국어 수행 준비 못해서 터지고, 누구는 그 반대고 하는 상황이 빈번하게 보인다.
당연히 이 동안 시험공부를 할 생각은 꿈에도 못 꾸고, 인강실에서 자바 프로젝트 마무리를 달리거나 하는 모습을 볼 수 있었다.
그렇게 힘들게 달려서 수행평가를 전부 끝내면 남는 것은?
시험공부를 할 일주일의 시간이다.
그 일주일동안 10~11개 과목 공부를 달리는 것은 결코 쉬운 일이 아닐 것이다.
"아니 그럼 공부를 미리 시작하면 되는거 아니야? 무슨 공부할 시간이 일주일밖에 없던 것도 아니고;;;" 라고 할 수 있겠지만,
수학여행에다가 기나긴 휴식의 시간을 가지고 나서 공부를 바로 시작하기는 쉽지 않은 일인데다가,
동아리 활동같은 것들에도 신경써야 하고, 이것저것 신경쓰고 나면 수행평가가 덮쳐오는 그림인지라 그게 또 쉽지가 않다.
하지만 지금까지 서술한 것들은 단지 표면상의 문제이다.
물론 힘들고, 공부하기 어려운 환경이 만들어지긴 했다.
하지만 그것과 어떻게 기가 막힌 콜라보를 하는 다른 문제가 생기는데, 바로 디미고의 "유통기한" 문제이다.
이게 대체 뭔소리냐고? 급식에 유통기한이 지나기라도 했냐고?
그런 이야기가 아니라, 아이들이 맛이 가기 시작한다는 이야기이다.
즉, 아이들의 유통기한이 다 되어가는 시점이 바로 이 고등학교 2학년 수학여행 전후 시점이다.
이쯤 되면 아이들의 정신 상태는 피폐해진다.
사실상 방학을 한 번 더 지낸 상황이 되는지라, 이미 게을러져 버린 아이들은 쉽사리 다시 공부 모드로 돌아가기 힘들고,
그런 아이들이 이제 학교에서 막 놀기 시작하는 시점이 오게 되는 것이다.
거기다가 기숙사 학교인 점도 어느 정도 작용을 하는 것 같다.
아무래도 기숙사 학교다 보니까 학교에서 하루 종일을 보내게 되는데, 너무 매일 있다 보니까 너무 익숙해지는 것 같다.
(아니면 수학여행이라는 극단적으로 학교와 다른 곳을 갔다가 다시 돌아와서 집으로 인식되는건가?)
1학년때야 익숙해지면 좋겠지만, 지금은 거의 집처럼 익숙해져 버려서 공부가 잘 되지 않는다는 문제점이 발생한다.
가끔 보면 야자 시간이 수면 시간이 되어 버린 날도 있을 정도이다.
그렇게 학교에 너무 익숙해져버린 아이들은 "유통기한"이 이미 끝나버려 기강이 해이해지게 된다.
실제로 야자 시간이나 방과후 자습 시간에 보면 많은 아이들이 정신 못차리고 자거나 노는 모습이 보인다.
...내 스스로의 모습도 그럴 때가 있다는 것이 부끄러울 따름이다. 그건 좀 반성해야지.
아무튼, 이런 여러 가지 이유들이 서로 맞물려서 최고(악)의 하모니를 이루며, 아이들의 멘탈을 털어버린다.
공부를 해야겠다고 생각은 드는데 공부는 하기 싫고, 막상 하려니 시간은 적은데 과목은 너무 많고...
진짜 미칠 지경이다.
이러면 수시를 버리면서 "나는 정시 파이터다! 깔깔깔!!" 하며 수시를 안드로메다로 날려버리는 아이들이 있는가 하면,
"오또케 오또케 수시 가고시푼데;;" 하며 저 멀리 떠나는 수시를 어떻게든 잡아보려는 아이들도 있다.
그럼 이 아이들은 다 어떻게 되냐고?
그건 나야 모르지 ㅎㅎ... 시험이 끝나봐야 알겠지?
이렇게 넋두리를 끝내고, 이젠 공부나 하러 가봐야겠다.
혹시 이 글 보는 후배 있으면, 진짜 2학년 1학기 기말 공부는 빨리 시작하라고 권고해주고 싶다.
너네들이라도 내신 잘 챙겨야지... 나는 그렇게 못했으니까 ㅠㅠ
'일상 > 디미고' 카테고리의 다른 글
| 디미고 진학 관련 이야기들 - 디미고 커트라인, 디미고 면접 등 (330) | 2019.11.04 |
|---|---|
| 디미고 입학설명회 후기 (0) | 2019.10.20 |
| 디미고 일상? - 노트북 편 (8) | 2019.04.24 |
| 디미고 일상 - 기숙사 밤 편 (3) | 2019.04.23 |
| 디미고 일상 - 시험 & 시험기간 편 (7) | 2019.04.22 |
CS234 Assignment 2-4 solution 및 풀이

1. [코딩] q3_nature.py의 get_q_values_op를 작성하여 [mnih2015human] 논문에 나와있는 대로 deep Q-network를 만들어보자.
나머지 코드들은 linear approximation에서 짠 코드 그대로 따라갈 것이다.
python q3_nature.py 명령어로 이를 CPU로 돌려보아라. 대략 1분에서 2분정도 걸릴 것이다. [10점]
sol) nature지 아래에 실린 architecture 란에 보면 :
The first hidden layer convolves 32 filters of 8 X 8 with stride 4 with the input image and applies a rectifier nonlinearity.
The second hidden layer convolves 64 filters of 4 X 4 with stride 2, again followed by a rectifier nonlinearity
This is followed by a third convolutional layer that convolves 64 filters of 3 X 3 with stride 1 followed by a rectifier.
The final hidden layer is fully-connected and consists of 512 rectifier units.
The output layer is a fully-connected linear layer with a single output for each valid action.
라는 설명이 있습니다.
이를 대충 해석하면,
첫번째 convolutional layer은 32 filters, 8*8 kernel size, stride 4, ReLU
두번째 convolutional layer은 64 filters, 4*4 kernel size, stride 2, ReLU
세번째 convolutional layer은 64 filters, 3*3 kernel size, stride 1, ReLU
마지막 hidden layer은 fully-connected layer로 512개의 output에 ReLU,
output layer은 각각의 action에 대한 single output이 나오는 fully-connected layer이라고 합니다.
이것을 코드로 구현하면 다음과 같은 코드가 나옵니다.
class NatureQN(Linear):
"""
Implementing DeepMind's Nature paper. Here are the relevant urls.
https://storage.googleapis.com/deepmind-data/assets/papers/DeepMindNature14236Paper.pdf
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
"""
def get_q_values_op(self, state, scope, reuse=False):
"""
Returns Q values for all actions
Args:
state: (tf tensor)
shape = (batch_size, img height, img width, nchannels)
scope: (string) scope name, that specifies if target network or not
reuse: (bool) reuse of variables in the scope
Returns:
out: (tf tensor) of shape = (batch_size, num_actions)
"""
# this information might be useful
num_actions = self.env.action_space.n
##############################################################
"""
TODO: implement the computation of Q values like in the paper
https://storage.googleapis.com/deepmind-data/assets/papers/DeepMindNature14236Paper.pdf
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
you may find the section "model architecture" of the appendix of the
nature paper particulary useful.
store your result in out of shape = (batch_size, num_actions)
HINT:
- You may find the following functions useful:
- tf.layers.conv2d
- tf.layers.flatten
- tf.layers.dense
- Make sure to also specify the scope and reuse
"""
"""
The first hidden layer convolves 32 filters of 8 X 8 with stride 4 with the input image and applies a rectifier nonlinearity.
The second hidden layer convolves 64 filters of 4 X 4 with stride 2, again followed by a rectifier nonlinearity
This is followed by a third convolutional layer that convolves 64 filters of 3 X 3 with stride 1 followed by a rectifier.
The final hidden layer is fully-connected and consists of 512 rectifier units.
The output layer is a fully-connected linear layer with a single output for each valid action.
"""
##############################################################
################ YOUR CODE HERE - 10-15 lines ################
input = state
with tf.variable_scope(scope,reuse=reuse):
conv1 = tf.layers.conv2d(input, 32, (8, 8), strides=4, activation=tf.nn.relu, name='conv1')
conv2 = tf.layers.conv2d(conv1, 64, (4, 4), strides=2, activation=tf.nn.relu, name='conv2')
conv3 = tf.layers.conv2d(conv2, 64, (3, 3), strides=1, activation=tf.nn.relu, name='conv3')
flat = tf.layers.flatten(conv3, name='flatten')
fc = tf.layers.dense(flat, 512, activation=tf.nn.relu, name='fully-connected')
out = tf.layers.dense(fc, num_actions, name='out')
pass
##############################################################
######################## END YOUR CODE #######################
return out
(보기 좋으라고 Class 선언부부터 넣어두지만, 구현한 부분은 가장 아래 10줄 가량입니다. input = state 부터...)
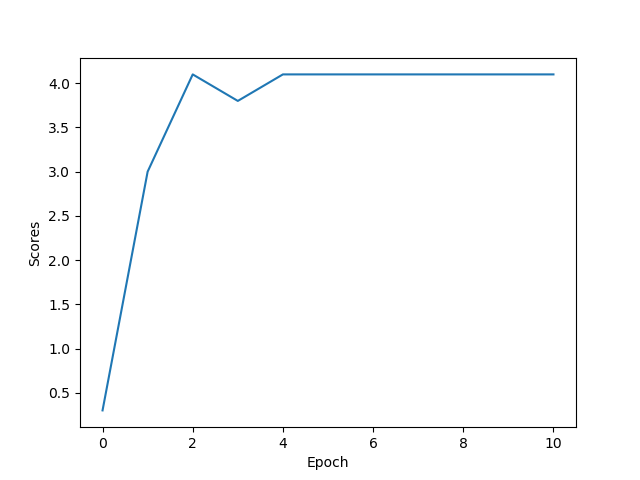
2. (written 5pts) Attach the plot of scores, scores.png, from the directory results/q3 nature to your writeup. Compare this model with linear approximation. How do the final performances compare? How about the training time?
2. results/q3 nature에서 scores.png 사진을 첨부하시오. linear approximation model과 비교하시오.
성능은 어떻게 차이가 나는가? 훈련 시간은 얼마나 차이가 나는가?
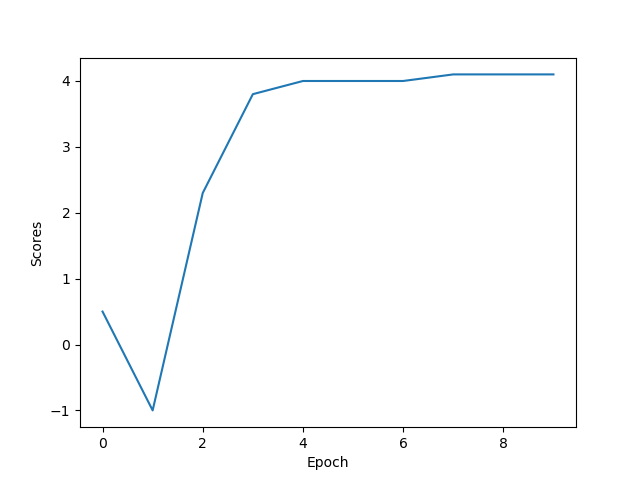
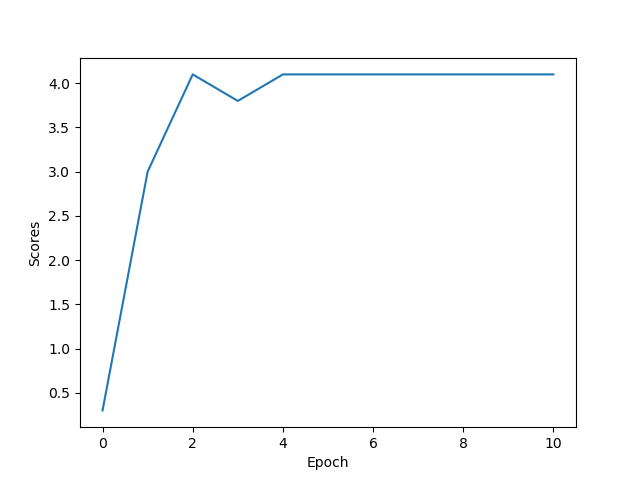
일단, DQN보다 Linear Approximation이 더 빠르게 converge 하기 시작하는 모습을 볼 수 있다.
심지어는 DQN을 돌릴 때 가끔씩 reward가 4.0에서 4.1로 가지 못한 채 training이 끝나는 모습도 볼 수 있었다.
아무래도 DQN이 Linear Approximation보다 더 unstable한 방식이라 그런 것 같다.
또한, training 시간도 DQN쪽이 더 오래 걸린다.
이것을 통해, 이렇게 간단한 test environment 같은 경우는 Linear Approximation이 더 잘 작동할 수도 있다는 것을 알게 되었다.
즉, environment에 따라 서로 다른 최적의 모델이 존재한다는 것을 알 수 있다.
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-3 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
CS234 Assignment 2-3 solution 및 풀이

1. x를 다음과 같이 정의할 때, ^q(s, a, w) = wTx(s, a)를 만족한다면 section 2의 (1) 식과 (2) 식이 동일하다는 것을 증명하시오. [3점]
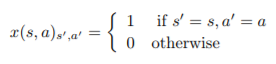
(수식이 너무 많아서 다 쓰긴 좀... 그냥 위에 있는거 대충 보고 합시다...)
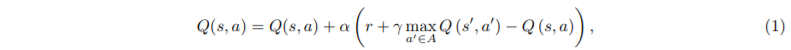
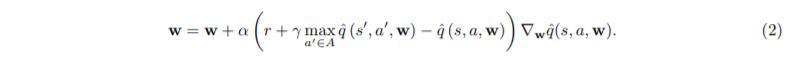
sol)
어차피 x(s, a)ₛ',ₐ' 가 0이 되면 w가 뭐든간에 ^q은 0이 되니까,
x(s, a)ₛ,ₐ = 1인 경우를 (2)번 식에 적용하면,
wₛ,ₐ= wₛ,ₐ + α(r + 𝛾max wₛ,ₐ - wₛ,ₐ)∇wₛ,ₐ wₛ,ₐ
(수식 ㅂㄷㅂㄷ;;; 대충 뭔뜻인지 이해하셨으면 좋겠는데... 그냥 ^q를 w로 바꾸고, w도 wₛ,ₐ로 바꾼 식...)
이 때, ∇wₛ,ₐ wₛ,ₐ = 1이므로 다시 정리하면
wₛ,ₐ= wₛ,ₐ + α(r + 𝛾max wₛ',ₐ' - wₛ,ₐ)
그리고 이를 다시 Q(s, a)로 정리하면 (1)번 식이 나온다.
2. qˆ(s, a, w) = wT x(s, a)이라고 할 때, value function parameter w ∈ Rⁿ에 대한 미분값을 구하고, w의 update rule을 적으시오. [3점]
sol) q^(s, a, w) = wTx(s, a)라고 했으므로,
∇w q^(s, a, w) = ∇w wTx(s, a) = x(s, a) 이다.
그리고 update rule은 아까 section 2 의 (2)번 식에 따라,
w = w + α(r + 𝛾max a0∈A qˆ(s 0 , a0 , w) − qˆ(s, a, w) )x(s, a)
가 된다. (그냥 뒤에 ∇w q^(s, a, w) 부분을 x(s,a)로 바꿈)
3. [코딩] 이제 tensorflow로 linear approximation을 구현할 것이다. 이 문제는 나머지 assignment 문제를 풀기 위한 pipeline을 작성하게 할 것이다. q2linear.py의 함수 중 다음의 함수를 구현할 것이다(q2linear.py를 읽어보라) :
• add_placeholders_op
• get_q_values_op
• add_update_target_op
• add_loss_op
• add_optimizer_op
작성한 코드를 python q2 linear.py 명령어를 사용해서 CPU에서 돌려보아라. 그러면 test environment에서 linear approximation을 실행시킬 것이다. 실행하는데 대략 1분에서 2분 정도 걸릴 것이다.
class Linear(DQN):
"""
Implement Fully Connected with Tensorflow
"""
def add_placeholders_op(self):
"""
Adds placeholders to the graph
These placeholders are used as inputs to the rest of the model and will be fed
data during training.
"""
# this information might be useful
state_shape = list(self.env.observation_space.shape)
##############################################################
"""
TODO:
Add placeholders:
Remember that we stack 4 consecutive frames together.
- self.s: batch of states, type = uint8
shape = (batch_size, img height, img width, nchannels x config.state_history)
- self.a: batch of actions, type = int32
shape = (batch_size)
- self.r: batch of rewards, type = float32
shape = (batch_size)
- self.sp: batch of next states, type = uint8
shape = (batch_size, img height, img width, nchannels x config.state_history)
- self.done_mask: batch of done, type = bool
shape = (batch_size)
- self.lr: learning rate, type = float32
(Don't change the variable names!)
HINT:
Variables from config are accessible with self.config.variable_name.
Check the use of None in the dimension for tensorflow placeholders.
You can also use the state_shape computed above.
"""
##############################################################
################YOUR CODE HERE (6-15 lines) ##################
batch_size = 5
img_height = state_shape[0]
img_width = state_shape[1]
n_channels = state_shape[2]
self.s = tf.placeholder(dtype=tf.uint8,
shape=[None, img_height, img_width, n_channels * config.state_history],
name='state')
self.a = tf.placeholder(dtype=tf.int32, shape=[None], name='action')
self.r = tf.placeholder(dtype=tf.float32, shape=[None], name='reward')
self.sp = tf.placeholder(dtype=tf.uint8,
shape=[None, img_height, img_width, n_channels * config.state_history],
name='next_state')
self.done_mask = tf.placeholder(dtype=tf.bool, shape=[None], name='done_mask')
self.lr = tf.placeholder(dtype=tf.float32, shape=(), name='lr')
##############################################################
######################## END YOUR CODE #######################
def get_q_values_op(self, state, scope, reuse=False):
"""
Returns Q values for all actions
Args:
state: (tf tensor)
shape = (batch_size, img height, img width, nchannels x config.state_history)
scope: (string) scope name, that specifies if target network or not
reuse: (bool) reuse of variables in the scope
Returns:
out: (tf tensor) of shape = (batch_size, num_actions)
"""
# this information might be useful
num_actions = self.env.action_space.n
##############################################################
"""
TODO:
Implement a fully connected with no hidden layer (linear
approximation with bias) using tensorflow.
HINT:
- You may find the following functions useful:
- tf.layers.flatten
- tf.layers.dense
- Make sure to also specify the scope and reuse
"""
##############################################################
################ YOUR CODE HERE - 2-3 lines ##################
input = tf.layers.flatten(state, name=scope)
out = tf.layers.dense(input, num_actions, name=scope, reuse=reuse)
##############################################################
######################## END YOUR CODE #######################
return out
def add_update_target_op(self, q_scope, target_q_scope):
"""
update_target_op will be called periodically
to copy Q network weights to target Q network
Remember that in DQN, we maintain two identical Q networks with
2 different sets of weights. In tensorflow, we distinguish them
with two different scopes. If you're not familiar with the scope mechanism
in tensorflow, read the docs
https://www.tensorflow.org/programmers_guide/variable_scope
Periodically, we need to update all the weights of the Q network
and assign them with the values from the regular network.
Args:
q_scope: (string) name of the scope of variables for q
target_q_scope: (string) name of the scope of variables
for the target network
"""
##############################################################
"""
TODO:
Add an operator self.update_target_op that for each variable in
tf.GraphKeys.GLOBAL_VARIABLES that is in q_scope, assigns its
value to the corresponding variable in target_q_scope
HINT:
You may find the following functions useful:
- tf.get_collection
- tf.assign
- tf.group (the * operator can be used to unpack a list)
(be sure that you set self.update_target_op)
"""
##############################################################
################### YOUR CODE HERE - 5-10 lines #############
q = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope=q_scope)
target_q = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope=target_q_scope)
assign = [tf.assign(target_q[i], q[i]) for i in range(len(q))]
self.update_target_op = tf.group(*assign)
pass
##############################################################
######################## END YOUR CODE #######################
def add_loss_op(self, q, target_q):
"""
Sets the loss of a batch, self.loss is a scalar
Args:
q: (tf tensor) shape = (batch_size, num_actions)
target_q: (tf tensor) shape = (batch_size, num_actions)
"""
# you may need this variable
num_actions = self.env.action_space.n
##############################################################
"""
TODO:
The loss for an example is defined as:
Q_samp(s) = r if done
= r + gamma * max_a' Q_target(s', a')
loss = (Q_samp(s) - Q(s, a))^2
HINT:
- Config variables are accessible through self.config
- You can access placeholders like self.a (for actions)
self.r (rewards) or self.done_mask for instance
- You may find the following functions useful
- tf.cast
- tf.reduce_max
- tf.reduce_sum
- tf.one_hot
- tf.squared_difference
- tf.reduce_mean
"""
##############################################################
##################### YOUR CODE HERE - 4-5 lines #############
notdone = 1 - tf.cast(self.done_mask, tf.float32)
action = tf.one_hot(self.a, num_actions)
q_samp = self.r + notdone * (self.config.gamma * tf.reduce_max(target_q, axis=1))
q_s = tf.reduce_sum(q * action, axis=1)
self.loss = tf.reduce_mean((q_samp - q_s)**2)
# self.loss = tf.squared_difference(q_samp, q_s)
##############################################################
######################## END YOUR CODE #######################
def add_optimizer_op(self, scope):
"""
Set self.train_op and self.grad_norm
Args:
scope: (string) scope name, that specifies if target network or not
"""
##############################################################
"""
TODO:
1. get Adam Optimizer
2. compute grads with respect to variables in scope for self.loss
3. if self.config.grad_clip is True, then clip the grads
by norm using self.config.clip_val
4. apply the gradients and store the train op in self.train_op
(sess.run(train_op) must update the variables)
5. compute the global norm of the gradients (which are not None) and store
this scalar in self.grad_norm
HINT: you may find the following functions useful
- tf.get_collection
- optimizer.compute_gradients
- tf.clip_by_norm
- optimizer.apply_gradients
- tf.global_norm
you can access config variables by writing self.config.variable_name
"""
##############################################################
#################### YOUR CODE HERE - 8-12 lines #############
optimizer = tf.train.AdamOptimizer(learning_rate=self.lr)
variable = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope)
gradient = optimizer.compute_gradients(self.loss, variable)
if self.config.grad_clip is True:
clip_grad = [(tf.clip_by_norm(i[0], self.config.clip_val), i[1]) for i in gradient]
self.train_op = optimizer.apply_gradients(clip_grad)
self.grad_norm = tf.global_norm([i[0] for i in clip_grad])
pass
##############################################################
######################## END YOUR CODE #######################
그냥 Linear class 전부 올리겠습니다. 어차피 저거 처음부터 끝까지 다 짜야되는거라;
파이썬 사용법에 그렇게 익숙치 않고, 텐서플로우를 잘 사용하지 않다 보니까 이것저것 다 찾아보며 하느라 힘들었네요.
4. test environment에서 얻을 수 있는 최적의 reward를 얻었는가? results/q2 linear에 있는 scores.png 파일을 첨부하여라. [5점]
sol...?) section 1에서 봤던 최적의 reward 4.1이 나오는 모습이다.
앞으로 얼마 안남았다.. 달려봅시다!
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-4 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
CS234 Assignment 2-2 solution 및 풀이

위에 나온 대부분의 내용들은 전 강의 DQN에 나와있는 내용이므로, 설명은 생략하겠습니다.
사실, 위에 나오는 건 그냥 배웠던 거 다시 설명하는 것 뿐이라...
설명하지 않았던 부분만 간단히 짚고 넘어간다.
실행 중에 (훈련하는 중에?), 버퍼에 (s, a, r, s') transitions을 집어넣는다. 새로 transitions가 들어오면 오래 된 transitions는 삭제된다. 파라미터들을 SGD update를 사용해 파라미터를 update할 때, 버퍼에서 minibatch를 sampling해서 update한다.
훈련 중엔 ε-greedy Exploration policy 를 사용하는데, deepmind의 논문에는 처음에는 ε=1로 시작했다가 백만 번 진행 중에 ε = 0.1까지 줄어든다. test할 때는, ε = 0.05로 두고 test한다.
참고 할 점들:
• 이 assignment에서는 replay 버퍼에서 minibatch를 sampling해서 w를 learning_freq 횟수에 한번 씩 update한다.
• Deepmind의 Deep Q network는 state s 를 input으로 받고, action의 갯수와 동일한 크기의 벡터를 output으로 낸다.
Pong environment에서는 action 6개가 있으므로, ^q(s, w)도 실수 범위 내에서 6개의 Vector를 가진다. (ℝ^6)
• 이 deep Q network의 input은 연속적인 4개의 step을 합친 것이고, 이를 preprocessing하면 (80 * 80 * 4)의 shape가 나온다.
1. experience replay를 사용할 때의 이점 한 가지를 대시오. [3점]
sol) 게임의 경우 전 프레임과 다음 프레임의 연관관계가 굉장히 끈끈한데, 이러한 연관관계는 SGD에 필요한 I.I.D 가정을 충족시키지 못한다.
이를 충족시키기 위해, experience replay를 사용하면 현재 프레임과 독립적인 프레임의 튜플을 update에 활용하여 SGD에 필요한 I.I.D 가정을 어느 정도 충족시킬 수 있다.
또, history에 저장되는 양을 늘림으로써 놓칠 수 있는 experience들을 다시 활용할 수도 있을 것이다.
(특히 prioritize experience replay를 사용하면 더 좋겠다.)
2. target network를 사용했을 때의 이점을 한 가지 대시오. [3점]
sol) Q-learning을 사용할 경우, update하는 과정에서 지속적으로 optimal한 값이 변화하게 된다. 그러면 w값이 막 미쳐돌아서 infinite로 날라갈 수도 있고, 굉장히 unstable해지는데, w값을 어느 정도 고정시켜주면서 이를 stable하게 잡아준다.
3. Q-Function을 ^q(s, w)∈ℝ^k 과 같이 나타낼 때의 이점을 한 가지를 대시오. [3점]
sol) 저렇게 벡터 형식으로 나타내면, 각각의 action에 대한 scalar값으로 나타내는 것 보다 연산 효율이 좋다.
4. (코딩문제) q1_schedule.py에 있는 get_action 과 update 함수를 구현하고, python q1_schedule.py로 구현한 것을 실행시켜 보시오. [3점]
참고 : http://web.stanford.edu/class/cs234/assignment2/assignment2.zip 에서 assignment2에 필요한 기초 코드를 받을 수 있다.
구현해야 되는 함수의 코드만 작성하겠다.
def update(self, t):
"""
Updates epsilon
Args:
t: int
frame number
"""
##############################################################
"""
TODO: modify self.epsilon such that
it is a linear interpolation from self.eps_begin to
self.eps_end as t goes from 0 to self.nsteps
For t > self.nsteps self.epsilon remains constant
"""
##############################################################
################ YOUR CODE HERE - 3-4 lines ##################
if t < self.nsteps:
self.epsilon = self.eps_begin - (self.eps_begin - self.eps_end) * t / self.nsteps
else:
self.epsilon = self.eps_end
##############################################################
######################## END YOUR CODE ############## ########위 코드는 ε-greedy policy를 더 fancy하게 만들기 위한 코드이다.
처음에는 epsilon값을 크게 잡아뒀다가, 가면 갈수록 점점 더 epsilon값을 작게 만들어 주는 것이다.
참고로 위 네 줄 짜리 코드는 다음의 세 줄짜리 코드로 줄일 수도 있다.
self.epsilon = self.eps_end
if t < self.nsteps:
self.epsilon = self.eps_begin - (self.eps_begin - self.eps_end) * t / self.nsteps
def get_action(self, best_action):
"""
Returns a random action with prob epsilon, otherwise returns the best_action
Args:
best_action: int
best action according some policy
Returns:
an action
"""
##############################################################
"""
TODO: with probability self.epsilon, return a random action
else, return best_action
you can access the environment via self.env
you may use env.action_space.sample() to generate
a random action
"""
##############################################################
################ YOUR CODE HERE - 4-5 lines ##################
if np.random.random() < self.epsilon:
return self.env.action_space.sample()
else:
return best_action
##############################################################
######################## END YOUR CODE #######################위 코드는 그냥 아까 전에 잡아둔 epsilon값을 바탕으로 action을 return하는 함수이다.
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-4 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-3 solution 및 풀이 (0) | 2019.06.07 |
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network)

- 본 포스팅은 CS234 6강의 내용을 정리합니다....만 CNN 부분은 따로 설명하지 않겠습니다.
그 대신, 제 블로그의 CS231n 강의 (https://cding.tistory.com/5) 를 보시거나 간단한 CNN 오버뷰 정도는 보고 오시면 좋겠습니다.

오늘 배울 것들로는 원래는 CNN과 Deep Q Learning이겠지만, 위에서 언급했듯 DNN 및 CNN은 설명하지 않고 바로 DQN으로 뛰어넘도록 하겠다.

그래서, DQN이 뭔지, 어떻게 이루어지는지 알아보자.

저번에 짤막하게 설명했듯이, function approximation, off policy control, boostrapping 셋을 모두 사용하는 것은 굉장히 unstable하다. Converge하지 않을 가능성이 농후하기 때문이다.
짤막하게 DQN의 역사에 대해 설명하자면,
1994년즘에 backgammon을 DQN으로 구현해낸 이후로 1995년 ~ 1998즘엔 위에서 말한 unstability를 개선하기 위한 연구를 진행하다가 DNN 자체가 망하는 바람에 연구가 더 진행되지 못했다.
그러다 2000년대 중반즈음부터 computational power의 증가 및 data의 증가 등의 이유로 DNN이 각광받기 시작하며,
DQN 또한 같이 주목받게 되었다.
그리고 2014년 (정말 얼마 안되었다) 경 Deepmind에서 위처럼 breakout (벽돌깨기) AI를 DQN을 사용해서 만들기에 이른다.
최근에는 도타 2 AI인 Openai five가 5대5로 프로게이머를 이기고, 전세계 사람들과 대전했을 때 99.5%의 승률을 자랑하기까지 하는 등 Deep Reinforcement Learning이 각광받고 있다.

아무튼, 우리는 DNN을 사용해서 Reinforcement Learning을 시킬 것이다.
(당연히 VFA를 사용한다.)

DQN은 그냥 Q (state action)을 DNN에 적용시킨 것 뿐이다. 그렇게 Value와 Q function을 구하는 것이 목적이다.


(대충 저번 시간에 했던 내용이므로 대충 생략하겠다는 말)

그래서 이러한 Q-Learning 방식을 Atari 게임에 적용시키면 된다.
게임 화면의 이미지를 state로, agent가 취하는 컨트롤을 action으로, 그리고 게임에서 주는 점수를 reward로 한다.
그렇게 해서 agent를 학습시켜 보자는 것이 기초적인 아이디어이다.
Atari Breakout (벽돌깨기) 을 예시로 들 것인데, Atari breakout같은 경우 action의 종류가 약 4개에서 18개정도밖에 되지 않는다.
하지만, state같은 경우 이미지의 픽셀값들을 받아오므로 굉장히 큰 data가 된다. 이것들을 어떻게 다뤄야 하는지 알아보자.

참고로 말해두자면, 지금부터 배울 대부분의 내용들은 2015년도 Deepmind의 Atari DQN 논문에 있는 내용들이다.
우선, input으로는 이전 4프레임의 이미지를 받는다.
1프레임의 이미지만을 input으로 두지 않고 이렇게 4프레임의 이미지를 받는 이유는 공의 방향이나 속도들을 알기 위해서이다.
CNN과 relu, fully-connected layer 등을 걸쳐 나오는 output은 Q(s,a)로, 18개의 조이스틱 및 버튼의 움직임을 표현한다.
그리고 Deepmind의 논문에서는, 이 아키텍쳐와 hyperparameter 들을 모든 게임에 동일하게 적용하였다.
그것만으로도 충분히 학습된다는 것을 보이기 위해서였고, 실제로 많은 게임들에 잘 적용되는 것을 볼 수 있다.
물론, 몇 개의 게임들은 확실히 tuning해야 할 것이다.
가령 delayed reward가 매우 중요한 게임들은 (감마) 값을 높게 두어야 할 것이다.

이제 진짜 본론으로 들어가보자.
Q-learning을 VFA를 사용해서, SGD를 사용해 MSE loss를 최소화시키고, 최적의 Q*(s, a)를 찾아가는 과정이다.
그러나, 저번에도 말했듯이 Q-learning을 VFA와 함께 사용하면 diverge할 수 있다. (수렴하지 않고 막 나간다)
그 이유는 첫번째로는, sample간의 연관성이 너무 크기 때문이다.
아까 전, 분명 DQN은 게임의 화면을 5프레임 간격으로 받는다고 했었는데, 분명히 게임의 연속된 다섯 프레임은 굉장히 연관되어 있을것이다.
그런데 이렇게 sample 간의 연관성이 너무 커져 버리면, SGD 방식으로 수렴하기 위해 필요한 IID 상태가 아니게 된다.
(IID란 간단히 말해서 모든 데이터들이 다 독립적이어야 한다는 뜻이다.)
또한, target이 non-stationary하다. 즉, target이 계속 변화한다.
VFA를 적용시키려면, 최소한 어디에 Converge시켜야 하는지는 알아야 한다.
그런데 Q-learning의 경우 이 optimal policy가 계속 바뀌므로, 어디다 Converge하기가 쉽지 않다.
이 두 가지 문제점을 해결하기 위해서, deepmind에서는 Experience Replay와 Fixed Q-target이라는 방법을 사용한다.

Experience Replay는, 말 그대로 지금까지의 경험을 축적해서 다시 사용하는 것이다.
원래였다면 그냥 한번 w와 policy를 update하고 말 경험들 (지나친 step들)을 저장하고 있다가, 나중에 다시 이 값들을 사용해서 w값을 update해 주는 것이다.
이렇게 하면 원래 굉장히 높은 연관성을 띄던 데이터들로부터 벗어나서, 조금 더 독립적인 (연관성이 적은) 데이터들로 다시 w를 update해줄 수 있는 것이다.
또, 원래 update하던 도중에도 Q-learning방식을 사용했기에 target value가 이미 바뀌어 있을 것이고, 그러면 그 바뀐 값에 대해 다시 독립적인 데이터를 사용해 w를 update해줄 수 있는 것이다.

Fixed Q-Targets는 말 그대로, target weight를 고정시켜주는 것이다.
Q-learning 방식에서는 계속 target이 바뀌어서 문제였지만, 이것을 그냥 고정시켜줌으로써 대처하는 것이다.
target update를 할 때 사용할 weight w⁻와 실제 update를 해 줄 weight w를 나누어서 사용하는 것이다.
아래쪽의 식을 보면 이해가 빠를 것 같다.
원래 max를 시켜주는 저 target에는 w⁻를 집어넣고, 그 외 나머지 부분에는 원래 weight w를 집어넣어 준다.
그리고, n번째 마다 (hyper parameter이다.) w⁻값을 다시 원래 w값으로 맞춰 준다.
이렇게 해 주면, 원래 Q-learning에서 계속 w가 바뀌다가 결국 w가 막 infinity로 터지는, 그런 상황을 방지할 수 있다.
즉, stability가 꽤 많이 향상된다는 것이다.

-정리-
DQN은 experience replay와 fixed Q-target를 사용한다.
replay memory D에 experience (s, a, r, s')을 채워주고, 거기서 mini-batch를 sampling해서 update한다.
또 fixed parameter w⁻를 사용하여 Q-learning target을 연산하고, MSE loss를 최소화 시켜준다.
SGD를 사용하고, (위에서 나오진 않았지만) ε-greedy exploration도 사용한다.
그러면, 이렇게 학습하면 잘 될까?
https://www.youtube.com/watch?v=V1eYniJ0Rnk
ㅇㅇ.. 잘 된다!

그럼 DQN에선 어떤 부분이 가장 중요할까?
위 표를 보면 알겠지만, experience replay를 적용시키는 경우 효율이 가장 좋은 것을 알 수 있다.

이제부턴, Deepmind의 논문 이후에 발표된, Deep RL의 주요 improvemets들을 설명하겠다.

그 중 첫번째는, 바로 Double DQN이다.
저번에 설명했던, maximization bias 문제를 해결하기 위해 나온 Double Q-learning의 Deep RL 적용판이다.

Double Q-learning이 뭐였는가?
Q를 하나만 쓰는 대신, 두 개를 사용하여 50% 확률로 Q1, 나머지 50% 확률로 Q2를 사용하여 Q-learning을 하는 방식이었다.

이 아이디어를 DQN에도 적용시킨 것이 바로 Double DQN이다.
현재 사용하는 Q-network w를 action을 고르는 데 사용하고,
w⁻는 action을 evaluate 하는 데 사용하는 것이다. (위 식 참고)

그래서, Double DQN을 사용하면, 위와 같이 좋은 결과를 낼 수 있다.

두 번째 방식은, 바로 Prioritized Replay이다.
말 그대로, Experience Replay를 그냥 막 골라서 하지 말고, 우선순위를 정해서 하자는 것이다.

이쯤, Mars Rover 예시를 다시 들어보자.
(지금까지 엄청 자주 설명했고, 위에도 잘 나오니 자세한 설명은 생락하겠다.)
그래서 위 예제에서 (s3, a1, 0, s2, a1, , s2, a1, 0, s1, a1, 1, terminal) 에피소드를 지난 뒤에, TD estimate는 어떻게 되는가?
한 번 update를 해 주면, 결국 reward가 s1, a1, 1, terminal 에서 나왔으므로 결국 [1 0 0 0 0 0 0]이 된다. (bootstrapping)
이제 여기서 replay를 두 번 진행할 수 있다고 할 때, 어떤 step을 replay하는 것이 가장 좋을까?
(오른쪽 위가 replay buffer가 저장되어 있는 모습이다.)
만약 (s3, a1, 0, s2) 버퍼를 사용해서 replay 한다면, 아무런 의미도 없을 것이다.
결국 지금 상태는 [1 0 0 0 0 0 0]이고, s3, s2는 reward가 0이므로, 아무런 영향도 미치지 않는다.
(s2, a1, 0, s2)를 선택하는 경우에도 마찬가지로, s2는 reward가 0이므로 아무런 영향도 미치지 않는다.
(s2, a1, 0, s1)을 선택하는 경우만 다르게 적용된다. 현재 s1이 1이므로, 이 reward 1은 그대로 s2에 전달되게 된다. (α=1)
그러면, 결국 TD estimate는 [1 1 0 0 0 0 0]이 된다.
그 다음엔?
만약 (s3, a1, 0, s2) 버퍼를 사용하면, s2의 reward가 1이므로, s3에도 그 reward가 그대로 전달되므로,
TD estimate는 [1 1 1 0 0 0 0]이 된다.
이렇게, 한 episode에서 최소의 replay buffer만을 사용하여 최적의 TD estimate를 얻어냈다.
만약 위처럼 우리가 replay buffer를 선택하지 않고 그냥 아무런 replay buffer나 사용하였다면, 이렇게 결과가 잘 나오진 못했 을 것이다.
위에서 아무런 영향을 주지 못한 replay는 결국 연산 횟수만 증가시키는 꼴이 되기 때문이다.
즉, 이렇게 replay buffer를 선택하는 과정은 update 효율을 굉장히 증가시켜 준다는 사실을 알 수 있다.

위에서 봤듯이, TD-learning에서는 replay의 순서가 학습의 속도를 늘리는 데 도움을 줄 수 있다.
아무런 쓸데 없는 정보가 담긴 버퍼를 사용하는 것 보다, 쓸데 있는 버퍼를 사용하는 것이 더 좋다는 것인데...
그런데, 어떻게 replay buffer의 우선순위를 정해야 할까?
위처럼 하나하나 넣어봐서 가장 좋은 버퍼를 고르는 것은 매우 비효율적일 것이니 말이다.

(대충 Episodic Replay Update의 순서를 정하는 것이 convergence를 빠르게 한다는 내용)

그래서 우리가 사용할 방법은 DQN error을 사용하는 방법이다.
어떤 tuple (replay buffer)를 골랐을 경우의 TD error와 현재 error의 차이가 가장 큰 것의 우선순위를 크게 잡아두는 것이다.
왜 이렇게 하냐고? 직관적으로 바라보자면...
만약 TD error가 현재의 error와 같다면 어떨까?
지금 선택한 replay buffer가 error에 아무런 영향을 끼치지 않는다는 이야기가 되므로, 정말 아무런 쓸데 없는 연산이 된다고 할 수 있다.
아까 위에 예시에서 아무런 영향을 끼치지 못하는 버퍼가 바로 이런 것들이다.
반면, TD error가 현재의 error와 크게 차이가 난다면?
그 버퍼가 바로 우리가 미처 제대로 습득하지 못한 데이터일 가능성이 커지게 되는 것이다.
그래서 이런 방식으로 replay buffer의 우선순위를 결정할 수 있다.
그럼 한 가지 질문만 던져보자. 만약 α=0이라면 어떻게 replay buffer가 선택이 될까?
α=0이라면, 저번 step에서 일어난 일이 현재 step까지 어떤 영향을 끼치지 못하게 되는 꼴이므로,
모든 TD-error과 현재 error의 차이가 동일하게 정해지게 된다.
그렇기에, replay buffer는 그냥 랜덤하게 결정되게 된다.

위는 Prioritized replay 방식과 double dqn 방식을 사용했을 때의 효과를 나타낸 그래프이다.
그냥.. 그렇다구...

다음으로, Dueling DQN이라는 방식이 있다.

이 방식의 요점은, optimal Q를 선택할 때 현재 state의 value와 action을 따로따로 생각한다는 점이다.
여기서 Advantage Function이 나오는데, 이는 Q(s, a)에서 V(s)를 뺀 값으로, 현재 action을 선택했을 경우 다른 action을 선택했을 때 보다 얼마나 더 좋은 결과를 내보내는지를 의미한다.
즉, 현재 Vπ(s)값에 비례한, action에 따른 상대적인 Value값을 의미한다.
개인적으로 이 부분 이해가 힘들었으므로 더 적어두자면, (사실 나중에 까먹었을때 볼라구 ㅎㅎ)
Vπ(s)는 policy를 따를 때, 그 state에서의 Value의 평균이다.
그리고 Qπ(s, a)는 각각의 action a를 따를 때 나오는 Value이므로,
결국 모든 action에 대한 Qπ(s, a) - Vπ(s) = 0이다.
여기서, 만약 Qπ(s, a)의 값이 Vπ(s)보다 크다면, 현재의 state에서 일반적으로 나올 수 있는 Value보다 더 좋은 Value를 얻은 action을 선택했다는 의미가 된다.
게임을 예시로 들어보자면,
현재 점수가 Vπ(s)인 것이고, Qπ(s, a)는 다음 action a를 취했을 때의 점수인 것이다.
만약 Advantage Function을 사용하지 않고 그냥 Qπ(s, a)만 본다면,
게임 후반의 점수가 게임 초반의 점수보다 당연히 더 높을 것이므로 게임 후반의 Q(s, a)값만 바라보고, 그 action을 취하는 데에 치중하게 될 것이다.
하지만 만약 Advantage Function을 사용하면, 게임 초반이나 후반이나 상관없이 내가 이 action을 취했을 때 얼마나 잘 플레이 한 것인지 알 수 있게 된다.

다음은 Dueling DQN의 아키텍쳐이다.
원래 DQN에서 마지막에 Q(s, a1), Q(s, a2) ...의 값이 나왔다면,
Dueling DQN에서는 마지막에 V(s), A(s,a1), A(s,a2)의 값들이 따로 나오고,
이 값들을 합쳐서 Q(s, a1), Q(s, a2)의 값을 얻어내는 것이다.


위 두 슬라이드는 영상에서 교수님이 설명을 안하셨다.
그러니 이해하고 싶으면 ppt를 보고 이해해야 된다.
난 못했으니 그냥 넘어간다.

Dueling DQN은 굉장히 효율이 좋은 학습 방식이고, 이는 위 그래프로 설명이 가능하다.

지금부터는 이 DQN을 실제 적용할 때의 팁들이다.
- DQN은 다른 방식들보다는 더 믿을만한 방법이다. Pong은 그중에서도 좀 믿음직 스러운 게임인데, 만약 DQN을 Pong에 적용시켰는데 뭔가 잘 안된다면, 너가 뭔가 잘못 한 것이다.
- DQN에서 replay buffer는 크면 좋으므로, 메모리 효율이 매우 중요하다. 데이터를 막 중복해서 쌓지 말고, uint8 이미지를 사용하라.
- DQN은 굉장히 천천히 Converge 하므로, 참을성 있게 기다려라.
아타리의 경우 천만~4천만 프레임 동안 기다려야지 random policy보다 훨씬 더 좋은 결과를 얻을 수 있는데,이는 GPU에서 훈련시킬 때 두시간 정도에서 하루 종일이 걸릴 정도의 양이다.
- 그리고 나중에 Atari를 실제로 학습시키려고 할 때, 작은 test environment에서 디버깅 꼭 해봐라.
이거 안하고 그냥 Atari에 때려 박았다가 잘 안되면 시간 날려먹는거니깐.

(이 ppt는 그냥 영상에서도 거의 거르다시피 함 - 알고 있거나 이해한 부분만 써놓음)
- Bellman error에서 Huber loss를 시도해 보아라. (위 식 참고)
- Double DQN을 써 보자 - 코드는 별로 안 바꿔도 되는데 성능 차이는 크게 난다.
- Learning rate scheduling은 꽤 좋다. 처음 exploration period에는 learning rate를 크게 잡아 놓아라.
이렇게 DQN에 대한 설명은 끝!
다른 강의들과는 조금 다르게 수학적으로 파고드는 것 보다 아이디어를 설명하는 강의였던 것 같다.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 8강 - Policy Gradient (1) | 2019.10.22 |
|---|---|
| 강화학습 강의 (CS234) 7강 - Imitation Learning / Inverse RL (1) | 2019.08.26 |
| 강화학습 강의 (CS234) 5강 - Value Function Approximation (4) | 2019.05.27 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
CS234 Assignment 2-1 solution 및 풀이
* 원래 해석 다 쓰고 쓸려 했는데 해석만 하다 보니깐 답답해 죽겠어서 그냥 풀면서 해석본 올리겠읍니다 ㅎㅎ..
어차피 딱 보니 제가 풀 클라스가 아닌 것들이 있는 것 같아서...
최종 해석본은 Assignment 풀이 끝나면 한번에 올리겠습니다.

1. Test Environment
다음과 같은 environment가 주어진다.
State 4개 : 0, 1, 2, 3
action 4개 : 0, 1, 2, 3, 4
action 0,1,2,3일때는 각각 state 0,1,2,3으로 가고, action 4일 때는 원래 state에 남아있는다.
reward는 위의 표를 참고하라.
한 episode는 time step 5번 (action을 5번 취한다)동안 지속된다.
또한, 언제나 state s0에서 시작한다.
(s, a, r, s')의 형태로 예시를 들면,
(0, 1, -0.2, 1, 2, 0, 2, 4, 0, 2, 3, 1, 3, 0 0.1, 0)
가 한 가지 예시이다. (자세한 것은 위의 그림을 참고하라.)
1. 위 test environment에서, 한 episode에서 얻을 수 있는 최대의 reward는? [5점]
sol) 다른 reward들은 죄다 -1 ~ 0.2 언저리에서 놀고 있지만, s2에서 a1을 취하는 경우는 reward가 2가 나온다.
어떤 경우에도 저 s2로 가서 a1을 취하는 것이 최선이다! (reward 0.2를 time step 5회에 걸쳐 계속 얻더라도 reward 2를 받는게 더욱 효율적이다)
그러므로, s0에서 시작하므로 s2로 우선 가는 것이 최선의 선택이다.
(s0, a2, 0, s2)
그리고 s2에서 a1을 취하면 reward 2를 얻을 수 있으므로,
(s0, a2, 0, s2, a1, 2, s1)
또 뒤에 time step이 3회나 남았으므로 다시 s2에서 a1을 취할 수 있으므로 다시 s2로 가서 a1을 취한다.
(s0, a2, 0, s2, a1, 2, s1, a2, 0, s2, a1, 2, s1)
이러면 time step은 1회가 남고, 이러면 그냥 이 상황에서 reward가 가장 높은 action을 고르는 것이 최선이므로,
s1에서 최선의 reward 0.1을 얻을 수 있는 action 0을 취하는 것이 최선의 선택이다.
(s0, a2, 0, s2, a1, 2, s1, a2, 0, s2, a1, 2, s1, a0, 0.1, s0)
그리고 이 때 얻는 reward는 0 + 2 + 0 + 2 + 0.1 = 4.1이다.
+추가로, 가장 처음에 s0에서 a0 또는 a4를 취해서 0.1을 먼저 얻은 뒤에 가는 경우도 고려하긴 해야 한다.
하지만, 그렇게 해도 (s0, a0, 0.1, s0, a2, 0, s2, a1, 2, s1, a2, 0, s2, a1, 2, s1)으로, reward가 4.1이 되니 결국 최대의 reward는 4.1이 된다.
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-3 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
| CS234 Assignments 1-1 Solution 및 풀이 (0) | 2019.04.25 |
CS234 Assignment 1-4 solution 및 풀이 (코드)
*Assignment 1-3은 본인의 수학적 실력 부족으로 인해 풀이까지 하긴 힘들 것 같습니다..ㅠㅠ
코딩 부분은 채워넣어야 하는 부분만 코드를 따로 올릴테니, 다른 추가 코드들은 직접 사이트에서 다운받아 주세요.
http://web.stanford.edu/class/cs234/assignment1/index.html
CS234: Reinforcement Learning
Assignment 1 Due Date: 1/23 (Wed) 11:59 PM PST. See course webpage for the late day policy. This assignment will provide you with practice with fundamental ideas in sequential decision making and the start of reinforcement learning. We will use Open AI gym
web.stanford.edu

(a) (코딩 문제) vi_and_pi.py를 읽고, policy_evaluation, policy_improvement, policy_iteration을 구현하라.
maxₛ |old_V(s) - new_V(s)|로 정의되는 stopping tolerance는 10⁻³이고, γ=0.9이다. optimal value function과 optimal policy를 return하여라. [10점]
def policy_evaluation(P, nS, nA, policy, gamma=0.9, tol=1e-3):
"""Evaluate the value function from a given policy.
Parameters
----------
P, nS, nA, gamma:
defined at beginning of file
policy: np.array[nS]
The policy to evaluate. Maps states to actions.
tol: float
Terminate policy evaluation when
max |value_function(s) - prev_value_function(s)| < tol
Returns
-------
value_function: np.ndarray[nS]
The value function of the given policy, where value_function[s] is
the value of state s
"""
############################
# YOUR IMPLEMENTATION HERE #
V = np.zeros(nS)
while True:
new_V = np.zeros(nS)
for state in range(nS):
for (prob, next_state, reward, end) in P[state][policy[state]]:
new_V[state] += prob * (reward + V[next_state] * gamma)
if np.all(np.abs(new_V - V) < tol):
break
V = new_V.copy()
############################
return new_V
def policy_improvement(P, nS, nA, value_from_policy, policy, gamma=0.9):
"""Given the value function from policy improve the policy.
Parameters
----------
P, nS, nA, gamma:
defined at beginning of file
value_from_policy: np.ndarray
The value calculated from the policy
policy: np.array
The previous policy.
Returns
-------
new_policy: np.ndarray[nS]
An array of integers. Each integer is the optimal action to take
in that state according to the environment dynamics and the
given value function.
"""
new_policy = np.zeros(nS, dtype='int')
############################
# YOUR IMPLEMENTATION HERE #
for state in range(nS):
Q = np.zeros(nA)
temp = -99
for action in range(nA):
for (prob, next_state, reward, end) in P[state][action]:
Q[action] += prob * (reward + gamma * value_from_policy[next_state])
if temp < Q[action]:
temp = Q[action]
new_policy[state] = action
############################
return new_policy
def policy_iteration(P, nS, nA, gamma=0.9, tol=10e-3):
"""Runs policy iteration.
You should call the policy_evaluation() and policy_improvement() methods to
implement this method.
Parameters
----------
P, nS, nA, gamma:
defined at beginning of file
tol: float
tol parameter used in policy_evaluation()
Returns:
----------
value_function: np.ndarray[nS]
policy: np.ndarray[nS]
"""
value_function = np.zeros(nS)
policy = np.zeros(nS, dtype=int)
############################
# YOUR IMPLEMENTATION HERE #
i = 0
new_policy = np.zeros(nS, dtype=int)
while i == 0 or np.sum(abs(new_policy - policy)) > 0:
policy = np.copy(new_policy)
value_function = policy_evaluation(P, nS, nA, policy, gamma, tol)
new_policy = policy_improvement(P, nS, nA, value_function, policy, gamma)
i += 1
############################
return value_function, new_policy
그냥 수식을 코드로 옮겼습니다.. 혹시 이 부분 구현이 잘못된 것 같다거나, 궁금한 점이 있으면 따로 댓글로 질문 부탁드립니다.
(b) (코딩 문제) vi_and_pi.py에서 value_iteration을 구현하여라. stopping tolerance는 10⁻³이고, γ=0.9이다. optimal value function과 optimal policy를 return하여라. [10점]
def value_iteration(P, nS, nA, gamma=0.9, tol=1e-3):
"""
Learn value function and policy by using value iteration method for a given
gamma and environment.
Parameters:
----------
P, nS, nA, gamma:
defined at beginning of file
tol: float
Terminate value iteration when
max |value_function(s) - prev_value_function(s)| < tol
Returns:
----------
value_function: np.ndarray[nS]
policy: np.ndarray[nS]
"""
policy = np.zeros(nS, dtype=int)
############################
# YOUR IMPLEMENTATION HERE #
V = np.zeros(nS)
while True:
new_V = np.zeros(nS)
for state in range(nS):
for action in range(nA):
temp=0
for (prob, next_state, reward, end) in P[state][action]:
temp += prob * (reward +gamma * V[next_state])
if temp > new_V[state]:
new_V[state] = temp
if np.all(np.abs(new_V - V) < tol):
break
V = new_V.copy()
policy = policy_improvement(P, nS, nA, V, policy, 0.9)
############################
return V, policy이것도 마찬가지로 그냥 ppt에 있던 수식을 그대로 코드로 구현했습니다.
처음에 state나 action 둘 중 하나만 for문을 돌렸다가 실패했던 기억이 있습니다.
(c) 각각의 방법 (vi와 pi)를 Deterministic-4x4-FrozenLake-v0과 Stochastic-4x4-FrozenLake-v0의 environment에서 실행시켜 보아라. 두 번째 environment에서, world의 dynamics는 무작위적(stochastic)이다. (world가 어떻게 움직이는지 랜덤이라는 뜻이다.) 이 무작위성은 반복의 횟수와 policy의 결과에 어떤 영향을 미치는가? [5점]
sol)
다음은 본인의 코드를 돌려 나온 결과값이다. (iter의 횟수를 count하는 코드는 위의 코드에는 없다..)
Deterministic-4x4-FrozenLake-v0
PI iter : 7
optimal Value Function
[0.59 0.656 0.729 0.656 0.656 0. 0.81 0. 0.729 0.81 0.9 0.
0. 0.9 1. 0. ]
Optimal Policy
[1 2 1 0 1 0 1 0 2 1 1 0 0 2 2 0]
VI iter : 7
optimal Value Function
[0.59 0.656 0.729 0.656 0.656 0. 0.81 0. 0.729 0.81 0.9 0.
0. 0.9 1. 0. ]
Optimal Policy
[1 2 1 0 1 0 1 0 2 1 1 0 0 2 2 0]
Stochastic-4x4-FrozenLake-v0
PI iter : 6
optimal Value Function
[0.062 0.056 0.07 0.051 0.086 0. 0.11 0. 0.141 0.244 0.297 0.
0. 0.377 0.638 0. ]
Optimal Policy
[0 3 0 3 0 0 0 0 3 1 0 0 0 2 1 0]
VI iter : 27
optimal Value Function
[0.062 0.055 0.07 0.051 0.085 0. 0.11 0. 0.14 0.244 0.297 0.
0. 0.377 0.638 0. ]
Optimal Policy
[0 3 0 3 0 0 0 0 3 1 0 0 0 2 1 0]
실제로 코드를 돌려 보면, Deterministic의 경우에는 Policy Iteration, Value Iteration 모두 한번에 Goal로 잘 도착한다.
하지만 Stochastic environment에서는 굉장히 머뭇머뭇하며 진행되는 경향이 있는 듯 하다.
Iteration 횟수는 Value Iteration같은 경우 증가했으나, Policy Iteration의 경우 1 감소했다.
VI에서 Iteration 횟수가 증가하는 것은 이해가 되지만, PI에서 왜 Iteration 횟수가 감소했는지는 잘 이해가 되지 않는다. (ㅠㅠ)
또한, environment의 stochastic하게 되면 Deterministic한 environment와 Optimal Policy도 달라지는 것을 확인했다.
VI와 PI가 동일한 Policy로 Converge한 것을 보면, 학습은 잘 된 것 같다.
(혹시 코드가 틀렸다거나... Policy Iteration에서 왜 Iter 횟수가 1 감소했는지 알려주실분 있으면 댓글 부탁드립니다... ㅠㅠ)
아무튼, 이것으로 CS234 assignment 1 풀이는 마치도록 하겠다.
이젠 assignment 2다!!
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignments 1-2 Solution 및 풀이 (0) | 2019.05.28 |
| CS234 Assignments 1-1 Solution 및 풀이 (0) | 2019.04.25 |
| CS234 Assignment 1 해석 (0) | 2019.04.19 |
CS234 Assignments 1-2 Solution 및 풀이
해석본은 아래 글에 찾아보시면 될 것 같습니다.
여기서는 풀이만 진행합니다.

(a) time step t=0인 state s0에서 action a1을 취할 때, 최종 discounted return (위 수식 참고)은 무엇인가? [5점]
sol) 처음 얻는 reward r0 = 0이고,
나머지 reward r1, r2, r3, ... , rt = 1이므로, 위 수식을 풀어 쓰면
0 + 𝛾 + 𝛾^2 + 𝛾^3 + .... = 𝛾 / (1-𝛾)
(b) time step t=0인 state s0에서 action a2를 취할 때, 최종 discounted return (위 수식 참고)은 무엇인가? optimal action은 무엇인가? [5점]
sol) 처음 얻는 reward r0 = 𝛾^2 / (1-𝛾)이고,
나머지 reward r1, r2, r3, ..., rt = 0이므로, 위 수식을 풀어 쓰면
𝛾^2 / (1-𝛾) + 0 + 0 + ... = 𝛾^2 / (1-𝛾)
그리고 0 < 𝛾 < 1이므로, 𝛾 / (1-𝛾) > 𝛾^2 / (1-𝛾) 이다.
즉, optimal action은 a1이다.
(c) 모든 state의 value를 0으로 초기화 했다고 가정하자. value iteration은 위의 수식 (n* ≥ log(1-ᵞ)/logᵞ ≥ 1/2 * log(1/1-ᵞ) * 1/(1-ᵞ)이 성립할 때 까지 sub-optimal action을 선택하는데, 이를 증명하여라.
따라서, value iteration은 1/(1-ᵞ)보다 빠르게 증가한다. (첫 번째 부등식이 옳다는 것만 보이면 된다.) [10점]
sol)
value iteration은 그때그때 최선의 value를 갖는 action을 고른다.
그렇기 때문에, Q(s0, a1) < Q(s0, a2)인 동안은 Value값이 높은 Q(s0, a2)를 계속 고르게 된다.
우선 action a2를 취할 때, s2에서 모든 Vn(s2) = 0이므로 Q값인 Qn+1(s0, a2)는 𝛾^2 / (1-𝛾)가 된다.
그리고, action a1을 취할 때의 value iteration은 다음과 같이 update된다 :
Qn+1(s0, a1) = 0 + 𝛾Vn(s1)
Vn+1(s1) = 1 + 𝛾Vn(s1)
즉,
Qn+1(s0, a1) = 0 + 𝛾(1 + 𝛾 + 𝛾^2 + ... + 𝛾^n)
= 𝛾 + 𝛾^2 + ... + 𝛾^n
= 𝛾 * (1-𝛾^n) / (1-𝛾)
그리고 딱 저 때의 n을 n*라고 두면, action a1을 취했을 때의 Q값이 a2를 취했을 때의 Q값보다 더 크거나 같아져야 하므로,
𝛾 * (1-𝛾^n*) / (1-𝛾) >= 𝛾^2 / (1-𝛾)
이것을 n*에 대해 정리하면 좌변과 우변의 1 / (1-𝛾) 는 사라지고,
𝛾 * (1-𝛾^n*) >= 𝛾^2 에서 양변의 𝛾를 나눠주면
1-𝛾^n* >= 𝛾
𝛾^n* <= 1-𝛾
n* >= log 𝛾 (1-𝛾) (log 밑이 𝛾, 진수가 1-𝛾) (0 < 𝛾 < 1이므로)
>= log (1-𝛾) / log(𝛾) (log 밑은 e)
이로써 첫 번째 부등식을 만족함을 보였다.
두, 세번째 부등식도 그냥 풀어가다 보면 만족함을 보일 수 있겠으나, 문제에서 첫 번째 부등식이 성립함을 보이기만 해도 된다고 했으니 걸러버리겠다.
'인공지능 > CS234 Assignments' 카테고리의 다른 글
| CS234 Assignment 2-2 solution 및 풀이 (0) | 2019.06.07 |
|---|---|
| CS234 Assignment 2-1 solution 및 풀이 (0) | 2019.05.29 |
| CS234 Assignment 1-4 solution 및 풀이 (코드) (0) | 2019.05.29 |
| CS234 Assignments 1-1 Solution 및 풀이 (0) | 2019.04.25 |
| CS234 Assignment 1 해석 (0) | 2019.04.19 |
강화학습 강의 (CS234) 5강 - Value Function Approximation

- 본 포스팅은 CS234 5강의 내용을 정리합니다.
* 기본적인 Neural Network 및 머신러닝 지식이 있으면 이해가 훨씬 빠릅니다! (그냥 알고 있어야 이해가 될것 같습니다 ㅎㅎ)

이번 강의에선 Value Function Approximation, 줄여서 VFA에 대해서 배운다.
주로 다룰 내용은 위 목차의 2번이 되겠다.
(3번은 시간 문제상 대부분 생략된다. 어뜨케 1강에서 5강까지 죄다 후반내용은 생략하시네 교수님;;)

지난 시간에, (CS234 4강의 내용) 경험을 토대로 좋은 policy를 얻는 방법을 배웠었다.
SARSA, Q-Learning, Monte Carlo, TD 등등...
그런데, 지금까지 이런 내용들을 배울 땐 value function이나 state-action value function을 벡터나 매트릭스 형태로 나타낼 수 있다는 가정 하에 배웠었다.
(이를 Tabular representation이라고 한다.)
그러나, 실제로는 value function이 그렇게 돼 있는 경우는 흔치 않다.
가령 자율운전 자동차를 만든다고 할 때, state가 얼마나 많겠는가?
왼쪽으로 1도 갔을 때, 2도 갔을 때.... 180도 갔을 때 등등만 하더라도 그렇겠지만,
거기다가 속도나 주변 차들의 유무 등등 수없이 많은 state들이 존재하게 될 것이다.
그렇기 때문에, 벡터나 매트릭스로 value function을 나타내는 tabular representation은 강화 학습의 실제 적용에 부족한 점이 있다.

이를 해결하기 위해서, 1강에 배웠던 Generalization을 사용하게 될 것이다.
이걸 왜쓰냐고? 일단 계속 보자.

Value Function Approximation이란, Value function을 state, action을 parameter로 갖는 function으로 만드는 것이다.
위의 사진을 보면 이해가 쉬울 듯 하다.
(V와 Q 위에 있는 건 hat이라고 하고, 예측값을 의미한다.)
Neural Network를 배우고 온 사람들이라면 이해가 쉬울 것이라 생각한다.
state, action s,a와 weight vector W를 이용해서 V,Q값을 계산하는 것이므로...
Neural Network와 상당히 비슷한 모습을 보인다.

이 짓 (VFA) 를 하는 이유는...
모든 state에서 Dynamics, Value, Q, Policy들을 명시적으로 알 필요 없이,
state와 state, function 을 모두 아우르는 간단한 일반항을 만들기 위함이다.
가령, V(s,w) 함수를 제대로 만들어 놨다면, 어떤 state에서도 그냥 저 V(s,w)에 s값만 대입하면 value가 그대로 튀어나온다.
즉, w 벡터 하나만 있으면 어떤 상황에서도 value가 그냥 나온다!

이렇게 Generalization을 하면 좋은 점은,
(P,R) / V / Q / π를 저장하는데 메모리가 덜 들고,
(P,R) / V / Q / π를 계산하는데 연산이 덜 필요하며,
좋은 (P,R) / V / Q / π를 찾을 때 experience가 줄어든다.
* 여기서 experience란 좋은 (P,R) / V / Q / π를 찾는 데 필요한 데이터의 수를 의미한다.
주의할 점은, 필요한 data의 수가 줄어든다고 하더라도 적은 데이터만을 갖고 VFA를 하게 되면, 좋지 못한 approximation이 될 수 있다는 것이다.
Neural network와 굉장히 유사한 느낌이라고 보면 될듯 하다.
데이터가 적게 들어와도 fitting을 잘 할 수 있겠지만 그렇다고 그게 실제 data에 잘 적용 가능한 approximation이 아닌것 처럼 말이다.
또한, 위와 비슷한 이유로 VFA를 사용하면 메모리 / 연산 횟수 / 데이터 갯수는 줄어들겠으나, representational capacity도 같이 줄어들게 된다.
*representational capacity는 머신러닝 모델의 flexibility, 즉 실제 데이터의 적응력 정도를 의미함.

그러면 VFA에 사용할 approximator에는 어떤 것들이 있을까?
Linear approximator를 사용할 수도 있고,
Neural Network를 사용할 수도 있고, Decision tree를 사용할 수도 있다.
이는 머신러닝 모델을 선택하는 것과 비슷한 맥락으로 볼 수도 있을 것 같다.
이 중에서 오늘은 Linear feature representation을 다룰 것이다.
(다음 시간에 Neural network도 다룬다.)

여기서 Gradient Descent에 대한 설명이 나오는데, 여기다가 다시 Gradient Descent를 설명하긴 좀 그렇고 하니 이미 아는 사람은 그냥 넘어가고, 모르면 다음 링크를 타고 들어가서 확인해보자.
https://cding.tistory.com/21?category=704767 - Gradient Descent
https://cding.tistory.com/56?category=704767 - 미분과 Gradient Descent에 대한 이해
왜 다 내 블로그 링크냐고?
아니 뭐 그럼 다른데 가서 보등가 ㅎㅎ...

일단 본격적인 VFA에 들어가기 앞서, 일단 쉬운 버전 먼저 시작해보자.
어떤 state s에 대해서든 완벽한 진짜 Value 값을 던져주는 오라클이라는 존재가 있다고 가정하자.
그리고 그 데이터들을 바탕으로, state s에 대해 value를 찾는 function을 구하려고 한다.
즉 state s가 주어졌을 때 value 값을 찾아내는 w의 값을 찾아내고 싶다는 것이다.

이렇게 하면, Supervised learning하는 과정과 거의 동일해진다.
오라클이 던져준 실제 V값과 우리가 구하고 싶은 Value function을 갖고 Gradient Descent 알고리즘을 적용하면 최적의Value function이 나올테니 말이다.
여기서 잠깐 Stochastic Gradient Descent (SGD)에 대한 설명이 나온다.
그냥 Gradient Descent 알고리즘은 모든 데이터의 cost값들과 미분값들을 토대로 w값을 update해 주었다면,
SGD는 모든 데이터가 아니라 랜덤하게 몇개의 데이터의 cost값들과 미분값들만을 가지고 w값을 update한다.
이렇게 하면 한번 update할 때 시간도 덜 걸리고, 일단 Gradient Descent와 거의 유사한 결과를 낼 수 있다.
근데 갑자기 이걸 왜 알려주냐고?
솔직히 나도 모르겠다 ㅎㅎ;

그런데 실제로 우리가 오라클이라는 존재를 알고 있진 않다.
즉, 실제 Value값을 알려주는 존재같은건 없다는 것이다.
이런 상황에서, 우리는 지금처럼과 같이 model에 의존하지 않고 model-free한 VFA를 만들 방법을 강구해야 한다.

그런데 Model-free.. model.... free...?
이거 우리 한번 하지 않았나?
맞다. CS234 3강의 내용이 바로 Model-free policy evaluation이었다!
그 때 우리는 Monte Carlo methods와 Temporal Difference methods, 줄여서 TD methods를 배웠었다.
이 방법을 그대로 VFA에 가져와서, update 과정에서 function approximator을 fitting하는 과정만 추가해서 사용하면 어떨까?
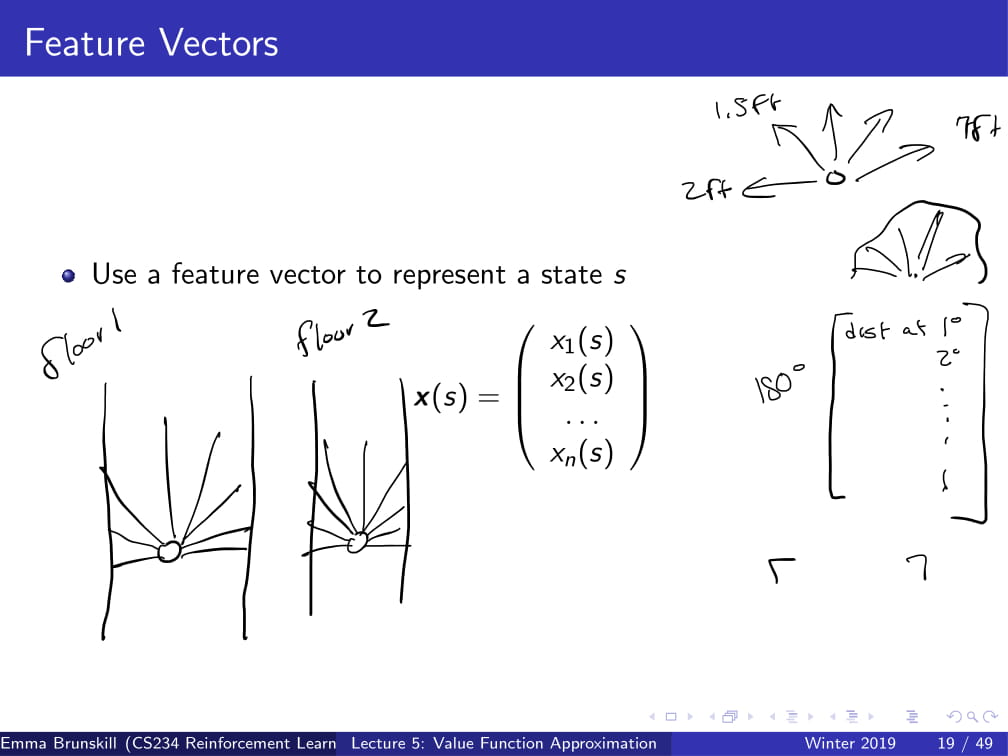
일단 들어가기 앞서 Feature vector이 뭔지 먼저 정의하고 넘어가겠다.
..라고 해도 그냥 별거 없다. 각각의 state에 대한 정보를 담고 있는 vector라는 뜻이다.
자동으로 청소를 해주는 로봇청소기를 예로 들어보자.
만약 이 로봇청소기에 왼쪽부터 오른쪽까지 전방 180도에 대한 거리를 알려주는 센서가 달려있다고 해보자.
그렇다면, 이 로봇청소기의 feature vector은 1도에서 180도까지의 거리가 될 것이다.
x1(s)에는 1도까지의 거리, x2(s)에는 2도까지의 거리 .... 처럼 말이다.
그리고 이것을 x(s)라고 정의해 두도록 하겠다.

그런데 일단, 오라클을 다시 데려와서 Value 값을 알려달라고 해보자.
그러면 위처럼 Value function의 approximation을 구할 수 있게 된다.
위의 내용이 대충 어떤 내용이냐면,
(대충 x(s)값을 사용해서 Supervised learning과 비슷하게 흘러간다고 설명하는 말)
자, 이제 이해했길 바란다.
절대 설명하기 귀찮아서 저렇게 둔 것이 아니다.

그런데 아까도 말했다시피, 우리한테는 오라클 같은건 없다.
그러니, 저번에 배웠던 Monte Carlo 방식을 사용해보자.
Monte Carlo 방식에서 return Gt는 unbiased, noisy한 Value 값이었다.
그리고, Monte Carlo는 지금까지의 경험을 그대로 Gt를 내놓는다.
즉, 이 Gt값은 어떤 state에 대한 true discounted Value 값이 된다.
(그러니까 이 Gt는 경험했던 state에 대해서만큼은 오라클이 던져주는 Value값과 동일한 실제 Value값이다.)
이를 사용하면, 아까 전에 했던 supervised learning과 동일한 방식으로 VFA를 적용할 수 있다.
(수식은 위 수식 참고)

위는 Monte Carlo 방식을 사용한 VFA가 어떻게 작동하는지 잘 알려준다.
사실 이건 딱히 말할 게 없다. 위에 너무 잘 적혀있으니 그냥 위 ppt를 보고 알아가도록 하고, 자세한건 나중에 나올 예시로 짚어보도록 할 것이다.
그래도 대충 설명을 하자면,
(대충 원래 MC에서 weight update가 추가된 것 뿐이라는 내용)
참고로 알아둘 사항만 적어두자면,
Line 5 : First-visit이라고 적혀있긴 하지만, Every-visit MC에도 동일하게 적용가능하다.
Line 7 : X(s)는 아까 했던 feature vector이다.

그럼 직접 예제로 알아보도록 하자.
위 그림 (s1, s2, s3 ... s7)을 통해서 봤을 때,
저 원 안의 수식은 각 state의 feature vector의 계산식을 의미한다.
w 값의 초기화를 [1 1 1 1 1 1 1 1]이라고 하면,
State s1의 feature vector는 [2 0 0 0 0 0 0 1],
State s2의 feature vector는 [0 2 0 0 0 0 0 1],
....
State s7의 feature vector는 [0 0 0 0 0 0 1 2] 가 된다.
action은 a1, a2 두가지가 있는데,
a1은 그림에서 실선으로 표시되며, 무조건 Deterministic하게 s7으로 가게 되고,
a2는 그림에서 점선으로 표시되며, 각각 1/6의 확률로 s1, s2, s3, ... , s6로 가게 된다.
또한, 어떤 state, 어떤 action에도 reward는 0이다.
그리고 우리는 이 상황을 Monte Carlo 방식을 사용해서 w의 값을 update하고 싶은데,
모두 알다시피 Monte Carlo 방식은 무조건 episodic한, 즉 termination이 존재하는 경우에만 사용이 가능하기 때문에
s7에서 a1을 취하면 0.999의 확률로 s7으로 가고, 0.001의 확률로 terminate가 된다고 가정하고 시작할 것이다.
이 때, 우리에게 다음과 같은 episode가 주어졌다고 가정해보자 :
s1, a1, 0, s7, a1, 0, s7, a1, 0, terminate
(State, Action, Reward 쌍이다.)
α = 0.5라고 할 때, w의 값은 어떻게 update되는가?
우선 state s1에서 return 값 G는 무엇인가?
모든 reward가 0이므로, return G도 0이 될 것이다.
그렇다면 s1의 value function의 초기값은 무엇이 될까?
w를 모두 1로 초기화한다고 했고,
s1의 feature vector( x(s1) )가 [2 0 0 0 0 0 0 1] 이었으므로
1*2 + 1*0 + 1*0 + ... + 1*1 = 3이 된다.
이쯤에서 아까 저 위에서 w값을 update하는 방식을 가져오면,
w = w + α(G(s) - V(s, a)) * x(s)
였으므로, 위에서 구한 값들을 여기에 대입하면
w = [1 1 1 1 1 1 1 1] + 0.5(0 - 3) * [2 0 0 0 0 0 0 1]
= [1 1 1 1 1 1 1 1] + -1.5 * [2 0 0 0 0 0 0 1]
= [1 1 1 1 1 1 1 1] + [-3 0 0 0 0 0 0 -1.5]
= [-2 1 1 1 1 1 1 -0.5]
...이렇게 w값이 update가 된다.
다른 episode들로도 한번 연습해 봐도 좋을 듯 하다.


위 두 슬라이드는 Linear VFA가 Converge하는가를 다루는 내용인데, 본인이 이해를 잘 못한 관계로 설명은 생략 ㅎㅎ...
강의 안볼거면 그냥 SGD를 사용하면 Linear VFA는 Linear이 할수 있는 최선으로 fitting된다는 정도로만 알아두자..
(물론 거의 무한하게 계속계속 update할 경우에 그렇게 된다는 거다..)

그런데 방금 전의 예시처럼 episode가 하나하나씩 들어오는 것들을 갖고 w를 update해도 되기야 하겠지만,
만약 episode들의 데이터가 있으면 그냥 그거 그대로 쭉 쓰면 안될까?
그러니까, episode를 하나하나씩 진행시키면서 update하지 말고 한방에 데이터들을 갖고 update할 수 있지 않을까?
...있으니까 말했겠지 뭐!
이를 Batch Monte Carlo Value Function Approximation이라고 부른다.
이름이 너무 길긴 하다..
이건 그냥 Linear Regression에 적용하듯, Analytic하게 적용이 가능하다.
위의 수식만 봐도 대충 이해 가능할 듯 하다.

Monte Carlo 방식은 여기까지만 알아보도록 하고,
이제 TD learning 방식으로 넘어가도록 하자.
일단 저번 저번 시간에 배웠던 TD learning을 잠깐 살펴 보자면,
TD learning은 DP 방식에서 사용하던 bootstrapping을 사용하며 MC 방식에서 사용한 sampling 방식도 사용했었다.

일단 본격적으로 들어가기 앞서, 지금까지 배운 세 가지 approximation을 생각보자.
1. (지금 하고 있는) function approximation
2. bootstrapping (DP / TD)
3. sampling (MC / TD)
그런데 지금 이 세개 모두 다 on-policy라는 것을 쉽사리 알 수 있을 것이다.
결국 지금 갖고 있는 데이터를 바탕으로 가는 것이니 말이다.
그러면, 결국 이 모든 것이 전부 supervised learning과 크게 다르지 않게 된다.
그렇다는 것은, 우리가 하고 있는 대부분의 것들 (위에 세가지) 는 convergence의 문제에서 어느 정도 자유로울 수 있다는 것이다. (거의 항상 수렴한다는 뜻)
그런데 이걸 왜 말해주냐고?
수렴하는지 안하는지 물어보지 말라고 하는 거 아닐까?

이제 본격적으로 들어가서,
원래 TD의 target (sampling)은 r + 𝛾Vπ(s') 이었다면,
VFA에서의 target은 r + 𝛾Vπ(s', w) (V위에 hat은 마음의 눈으로 보자 ㅎ)가 된다.
즉, w값도 찾아야 한다, 이말이다.
아무튼 이렇게 J(w)의 값을 최소화시키는 w값을 찾아가는 것이 바로 TDVFA이다. (길게 쓰기 싫어서 줄여씀)

그냥 위 식을 막 바꾸다 보면 아래까지로 바꿀 수 있다는 뜻 ㅎ
이건 TD때 비슷하게 했으니 그냥 넘기겠읍니다 ^^7

그리고 이를 의사코드로 바꾸면 위처럼 쓸 수 있다.
아까 전의 ppt 내용과 동일하다는 것을 알 수 있다. (거의)

아까 전의 그 예제로 돌아가보도록 하자.
기억이 안난다고?
예제 설명한거 복사해서 메모장에 붙여넣고 해보도록 하자 ㅎ
뭐 아무튼, 그 상황에서 MC 대신 TD learning을 적용해보자.
(참고로, 이번 상황에선 MC가 아닌 TD를 사용하므로, 0.999 어쩌구 하는 부분은 걸러도 된다. episodic 하지 않아도 되니깐 ㅎ)
episode는 [s1, a1, 0, s7]이라고 가정하고, 𝛾=0.9라고 하자.
그러면, w의 update는 어떻게 될까?
위의 수식을 그대로 빼다 박으면,
Δw = 0.5 * (0 + 0.9 * ([0 0 0 0 0 0 1 2] T [1 1 1 1 1 1 1 1]) - [1 0 0 0 0 0 0 2] T [1 1 1 1 1 1 1 1]) * [1 0 0 0 0 0 0 2]
= 0.5 * (2.7 - 3) * [1 0 0 0 0 0 0 2]
= 0.5 * -0.3 * [1 0 0 0 0 0 0 2]
= [-0.15 0 0 0 0 0 0 -0.3]
그리고 이 Δw를 w에다가 더하면,
w = [0.85 1 1 1 1 1 1 0.7]
이런 식으로 바뀌는 것이다.

TD에서도 특정 값에 수렴하는 성질이 있다.
여기두 본인이 이해가 잘 안되는 관계로 생략 ㅎ..
참고로 짤막하게 지나가지만, TD가 MC보다 조금 더 좋은 성적을 내는 경향이 있다.
(그냥 조금 더 좋다)

이제 Control 부분을 다뤄 보도록 하자.
일단 들어가기 앞서서, Function approximation / Bootstrapping / Off-policy learning 을 한번에 적용하려 하면 불안정해질 수도 있다.
그러니까, converge가 안 될 수도 있고, 잘 될 수도 있다는 것이다.

그리고 Control을 할 때, 우리는 Q function을 사용할 것이다. (Action-Value 쌍)
일단 오라클이라는 존재가 우리에게 답을 알려준다면, 어떻게 하면 될까?
아까 전까지 했던 것과 거의 똑같이 하면 된다.
실제 Q값에서 Q의 예측값을 빼서, w값을 최소화시켜주면 되는 것이다.
(위에서는 SGD를 사용한다.)

오라클이 없다면?
아까처럼 feature vector을 만들어야 한다는 점은 동일하지만,
x(s) = [x1(s), x2(s) ... ] 가 아니라, state-action 쌍을 이루도록
x(s, a) = [x1(s, a), x2(s, a) ... ] 로 만들어 둔다.
그 외의 나머지 부분도 아까 전과 동일하다.

그리고 위의 내용들도 아까 전에 했던 것과 4강때 했던 것과 배우 비슷하다.
단지 Return값 Gt와 target이 Q와 관련된 식으로 변화하였고,
function approximator을 추가해줬을 뿐이다.
이쯤에서 5강 내용은 마치도록 하겠다.
본인이 이해를 못한 부분이 꽤 있어서, 이 뒤 부분은 사실 설명을 잘 할 자신이 없다.
나중에 다시 한번 정리하면서 수정할 날이 오면, 더 보충설명을 진행하도록 하겠다.
'인공지능 > 강화 학습 정리 (CS234)' 카테고리의 다른 글
| 강화학습 강의 (CS234) 7강 - Imitation Learning / Inverse RL (1) | 2019.08.26 |
|---|---|
| 강화학습 강의 (CS234) 6강 - CNN + DQN (Deep Q Network) (0) | 2019.06.06 |
| 강화학습 강의 (CS234) 4강 - MC / SARSA / Q-learning (1) | 2019.05.08 |
| 강화 학습 강의 (CS234) 3강 - Model-Free Policy Evaluation (Monte Carlo / Temporal Difference) (3) | 2019.04.21 |
| 강화학습 강의 (CS234) 2강 - Markov Process / MDP / MRP (2) | 2019.04.15 |